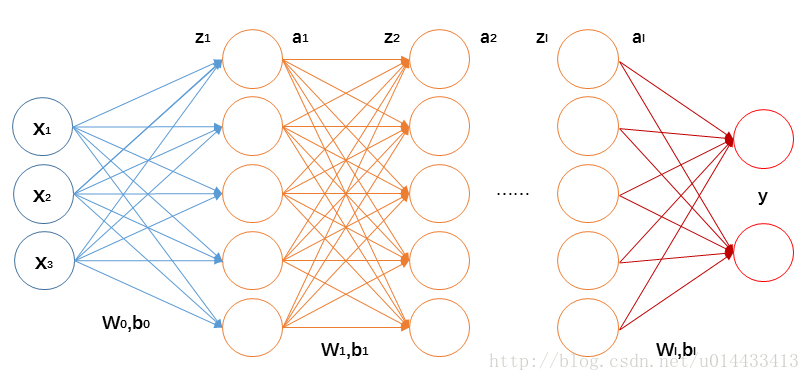
1 前向傳播

這裡的推導都用矩陣和向量的形式，計算單個變數寫起來太麻煩。矩陣、向量求導可參見上面參考的部落格，個人覺得解釋得很直接很好。

前向傳播每一層的計算如下：

f 是啟用函式。一般有sigmoid、tanh、relu等。

2 反向傳播

為了得到好的模型，我們要更新引數 W,b ，這裡就用到了反向傳播。

我們將神經網路的損失函式記為 J(W,b) ，這裡的 W,b 是指網路中所有的引數。損失函式可以是均方誤差、交叉熵等等。總之是衡量網路輸出的結果與真實標記之間的差異。

之後，就要計算 J(W,b) 對每一層 W,b 的梯度，對 W,b 進行更新。所有引數更新完成後，再進行前向傳播。迴圈往復，直到達到要求為止。

反向傳播之所以和正向傳播這麼對比著說，是因為反向傳播也是一層一層地計算。首先看最後一層（假設最後一層沒有啟用）：

我們記：

通過（1.1）和（1.2）我們可以得出：

將（2.3）-（2.5）代入（2.1）、（2.2）得：

下面我們看倒數第二層：