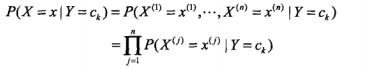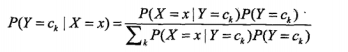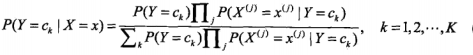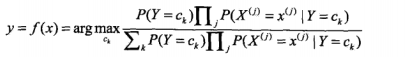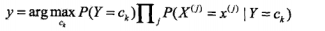注：本文中所有公式和思路來自於李航博士的《統計學習方法》一書，我只是為了加深記憶和理解寫的本文。

樸素貝葉斯(naive bayes)是基於貝葉斯定理和特徵條件獨立假設的分類器，對於給定的訓練資料集，首先基於特徵條件獨立假設學習輸入\輸出的聯合概率分佈；然後基於此模型，輸入x，利用貝葉斯定理求出最大後驗概率y。

樸素貝葉斯這個名字乍一看感覺蠻奇怪的，何為“樸素”呢？因為樸素貝葉斯有兩個很強的假設：一是特徵之間條件獨立，二是特徵之間權重相同，因此得名。於是我們可以用下面的公式表達這個假設：

其中X為樣本空間X={x1,x2,x3..xn}，Y為標記空間Y={c1,c2,c3...ck}，這裡邊的c說白了就是類別，如果是垃圾郵件系統就是1(垃圾郵件)、0(非垃圾郵件)，如果是論壇評論1(垃圾)、0(非垃圾)，j表示x的取值，可以是本字典，也可以是當前系統的詞集，僅此而已。

樸素貝葉斯是生成模型，因為本質是學習了生成資料的機制，條件獨立假設就意味著如果給定了條件，那麼分類的特徵就是相互獨立的，雖然使得模型簡單了一些，但是會損失一定的準確率，就像我說“機器”那麼下個詞說“學習”的概率是很大的，是不獨立的，在樸素貝葉斯法中我們視為獨立的。

輸入x，通過學習的模型來計算後驗概率P(Y=ck | X=x)，將後驗概率最大的類輸出，公式為：

那麼將第一個公式帶入第二個公式則有：

這是樸素貝葉斯的基本公式，那麼樸素貝葉斯分類器就可以表示為：

但是在由於我們只是分類而不輸出實際的後驗概率的話，就可以去掉分母，因為對於求最值來說，分母都一樣，沒必要留著，於是可以簡化成下邊的公式：

是不是特別簡單，對的，就是這麼的簡單，而且在垃圾郵件分類或論壇留言過濾還是很有效的。

但是需要注意幾個地方：

1. 如果有10000個詞，每個詞條件概率又很小，那麼連乘的話早就下溢位了，如何破？

答：可以取對數

2. 如果J中的詞有的沒出現過，那麼就是0，一乘可就全部為0了？

答： 可以使用拉普拉斯平滑，如果用n1表示一詞在某分類中的詞典出現的次數，n表示該類的總詞數，J為所有類別總詞數，那麼可以以(n1+1)/(n+J)

3. 如果一個詞在文中出現多次和一個詞只出現一次的詞向量相同怎麼辦？

答： 改01為計數

4. 如何判斷兩個文件的距離？

答：夾角餘弦

5. 如何確定分類器的正確率？

答：交叉驗證

樸素貝葉斯優缺點：

優點：

對小規模的資料表現很好，適合多分類任務，適合增量式訓練。

缺點：

對輸入資料的表達形式很敏感（離散、連續，值極大極小之類的）