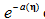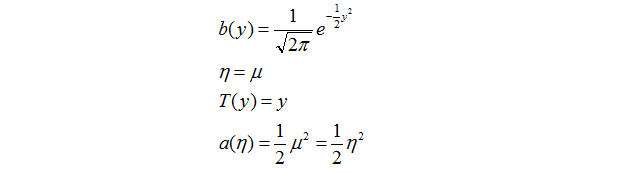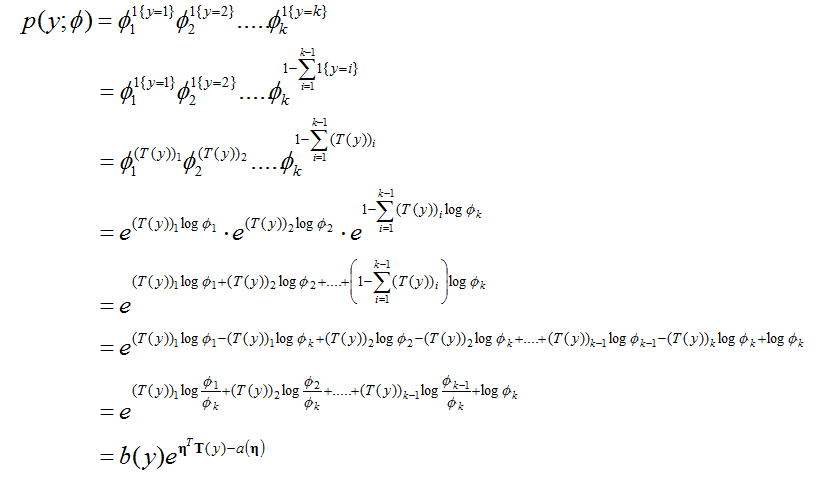機器學習筆記五:廣義線性模型(GLM)
一.指數分佈族
在前面的筆記四里面,線性迴歸的模型中,我們有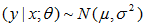
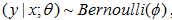
如果一類分佈能夠寫成如下的形式,那麼這個分佈就能夠被劃歸到指數分佈族裡面。
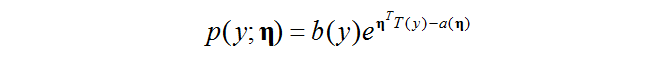
其中:
η 被稱為這個分佈的自然引數(natural parameter)或者canonical parameter
T (y) 被稱為充分統計量(sufficient statistic) (在我們暫時用到的模型裡面,你可以認為他就是 that T (y) = y)
a(η) 被稱為log partition function.起到歸一化常數的作用,確保這個分佈累計起來為1。
當T , a,和b被選中固定之後,也就確定了一個分佈的族,且以η為引數。如果我們改變η,我們就得到了不同的分佈。
接下來我們看看怎麼證明開始的那個伯努利分佈和高斯分佈是指數分佈族裡面的。
首先來看看伯努利分佈:
伯努利分佈可以寫為一下的形式:
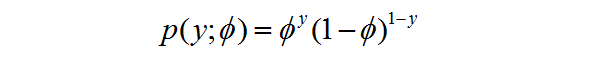
其中y的取值為0或者1,這個太簡單了,就不多解釋了。我們的目標就是選擇a,b,T,使得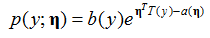
首先伯努利分佈可以寫成:
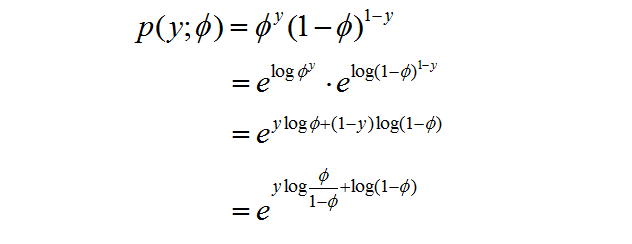
看這個式子的形式,把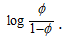
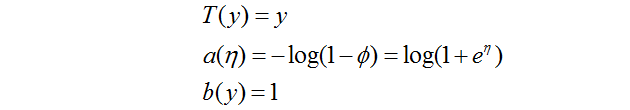
可以發現,伯努利分佈確實能夠寫為指數分佈族的形式。
這裡有個很重要的地方就是,因為自然引數是選擇為
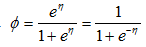 ,你是不是看到了一絲絲sigmoid/logistic函式的樣子?這個後面還會要用到。
,你是不是看到了一絲絲sigmoid/logistic函式的樣子?這個後面還會要用到。
接下來就是高斯分佈了。
要知道,線上性迴歸的例子裡面,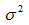
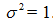
我們有:
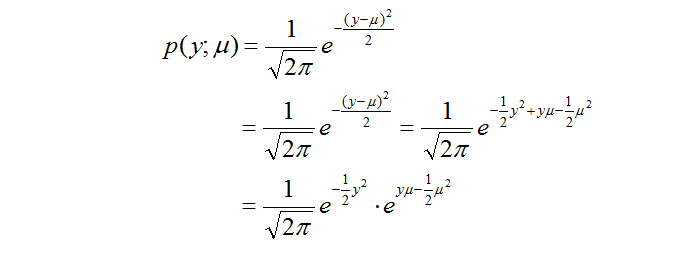
從上面的式子裡面已經可以看出高斯分佈是處於指數分佈族裡面的了,其中
總結一下,其實除了這兩個以外,還有很多的分佈都是在指數分佈族裡面的。比如多項式分佈,泊松分佈,指數分佈,gamma分佈和beta分佈等等一些。。。
二.構造廣義線性模型(GLM)
對於一個迴歸或者分類的問題,我們希望通過x的函式預測隨機變數y的值。首先我們需要作出如下幾個假設:
1.
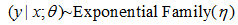 ,這個假設的意思是對於給定的x和θ,y的分佈要隸屬於以η為引數的指數分佈族。(不然上面講那麼多指數分佈族幹嘛?)
,這個假設的意思是對於給定的x和θ,y的分佈要隸屬於以η為引數的指數分佈族。(不然上面講那麼多指數分佈族幹嘛?)
2.對於給定的x,我們的目標是得到的輸出滿足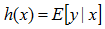
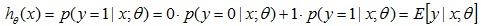
3.自然引數η和輸入x滿足線性關係: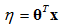
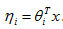
有了上面的3個假設之後,下面來看看線性迴歸,logistic 迴歸以及新的一種很常見的softmax迴歸是怎麼從廣義線性模型得到的。
Ⅰ.線性迴歸
由本節開頭的結論(詳細過程的看上一個筆記),線性迴歸中有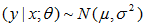
直接用上面的3個假設,有
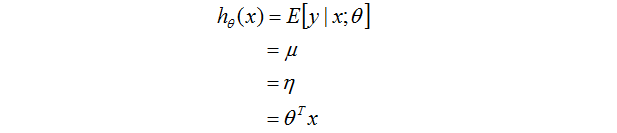
第二行的等式是高斯分佈性質
第三行等式在推導高斯分佈屬於指數分佈族裡面的結果。
最後一行等式是利用的上面的第3個假設。
你看這個h函式是不是和之前的線性函式是一樣的。。。。
Ⅱ..logistic迴歸
最開始要說的就是,這裡的推導要結合上面的那幾個假設來看。
對於之前提到的logistic迴歸,我們知道他的結果是二值的,即y ∈ {0, 1},那麼很自然的選擇伯努利分佈來為給定x下y的條件分佈建模。
最開始我們就知道了,伯努利分佈是是隸屬於指數分佈族的,所以我們這裡就滿足了上面的假設1。
如果: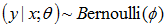
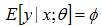
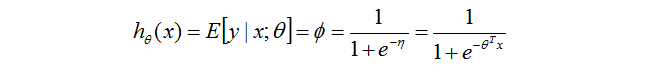
上面這個式子用到了假設2,假設3和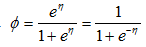
然後你直接看這個函式,是不是就是logistic的函式?
這裡給出一個概念:
the function g giving the distribution’s mean as a function of the natural parameter (g(η) = E[T (y); η]) is called the canonical response function(規範響應函式). Its inverse is called the canonical link function(規範連線函式).
暫時總結一下,高斯分佈族的規範響應函式是恆等函式(identify function),伯努利分佈族的規範響應函式是logistic函式。
Ⅲ.softmax迴歸
前面說過的分類問題都是處理那些分兩類的問題。比如區分貓或者狗的問題,就是一類是或者否的問題。但是現實生活中還有更加多的多類問題。比如貓分類,有田園貓,布偶貓,暹羅貓各種貓,這裡就不能夠用兩分類來做了。
這裡先設問題需要區分k類,即y ∈{1 2, … , k}。如果是你,你會用什麼分佈來建模呢?無疑是多項式分佈(multinomial distribution)。
為了通過k個可能的輸出給多項分佈確定引數,一個方法是可以使用k個引數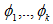
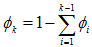
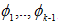
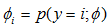
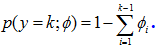
為了把多項分佈表示為一個指數分佈族,定義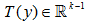
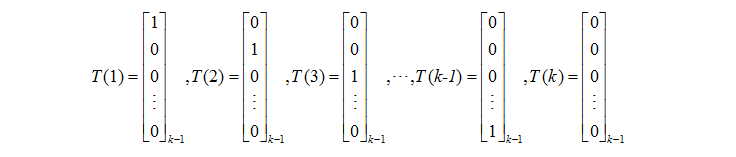
後面,我們用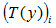
為了簡便,這裡引入一個指示函式(indicator function),他的定義是這樣的。
1{·} takes on a value of 1 if its argument is true, and 0 otherwise(1{True} = 1, 1{False} = 0).
比如 1{2 = 3} = 0還有就是1{3 =5 - 2} = 1等等
那麼就有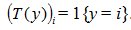
可能很多人都會有點蒙這裡。舉個栗子,
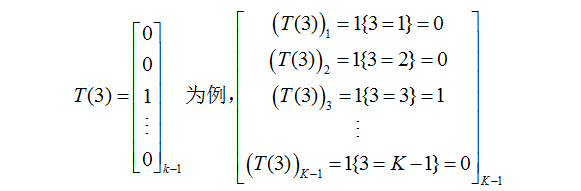
(這裡可能需要花點時間理一理。其實本質是很簡單的。)
更深一步可以得到:
有了上面的準備之後,就能夠直接推導初多項分佈的指數分佈族的形式了,如下:
其中:
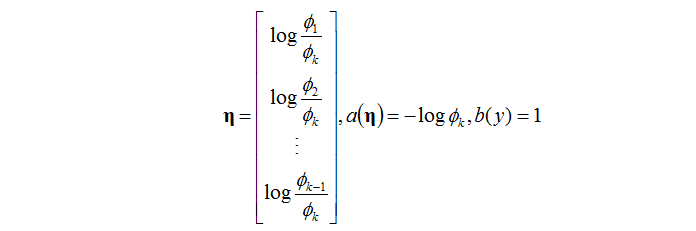
這個就說明了,多項分佈也是“隸屬於”指數分佈族的。
link function(i=1…k)有下面式子給定
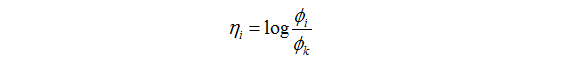
很容易知道
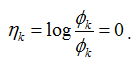
接下來我們需要得到響應函數了,有:
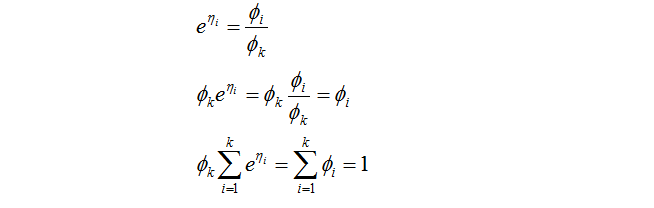
那麼最終得到
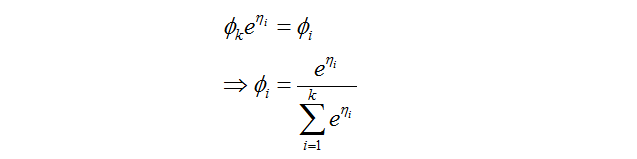
這個函式被稱為softmax函式。