problem

在一個無向圖\(G=(V,E)\)中，可以改變\(k\)條邊的權值為\(\Delta w\)，求單源最短路徑。

solution

分層圖的想法就是如果有\(k\)條邊就建\(k+1\)層圖

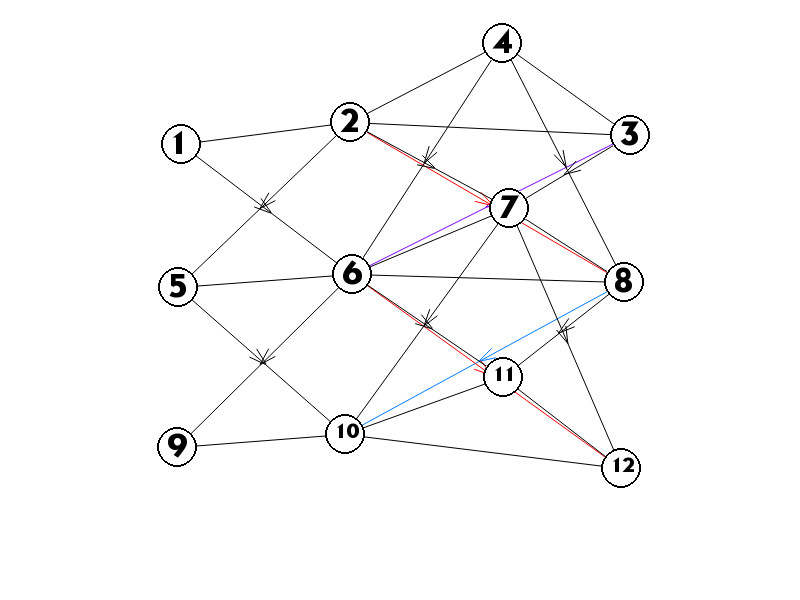
這個圖實際上是這樣的，對於每層中相連的點\((u,v)\)連權值為\(w\)的無向邊，在本層圖中相連的點\((u,v)\)由上層點\(u\)向下層點\(v\)以及上層點\(v\)向下層點\(u\)連權值為\(\Delta w\)的有向邊，方向是從上層向下層。
這樣構造完成一張分層圖後，從第\(1\)層的起始點\(s\)求單源最短路徑，最終第\(k + 1\)層的終點\(t\)的單源最短路徑值即為答案所求。
原理其實很簡單，如果從上層圖到下層圖，有向邊\((u,v)\)

T1

P2939 [USACO09FEB]改造路Revamping Trails

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;
const int N = 1e4 + 5, M = 5e4 + 5, K = 105;
int n, m, k;
struct Edge {
    int Next, to, dis;
}e[M * K * 2];
int head[N * K], num;
void add(int from, int to, int dis)
{
    e[++num].Next = head[from];
    e[num].to = to;
    e[num].dis = dis;
    head[from] = num;
}
int dist[N * K], vis[N * K];
struct node {
    int u, d;
    bool operator < (const node &x) const {
        return d > x.d;
    }
};
priority_queue<node> q;
void dijk()
{
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    q.push((node){1, 0});
    while(!q.empty())
    {
        int u = q.top().u; q.pop();
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = head[u]; i; i = e[i].Next)
        {
            int v = e[i].to, w = e[i].dis;
            if(dist[v] > dist[u] + w)
            {
                dist[v] = dist[u] + w;
                if(!vis[v]) q.push((node){v, dist[v]});
            }
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1, u, v, z; i <= m; i++)
    {
        scanf("%d%d%d", &u, &v, &z);
        add(u, v, z); add(v, u, z);
        for(int j = 1; j <= k; j++)
        {
            add(j * n + u, j * n + v, z);
            add(j * n + v, j * n + u, z);
            add((j - 1) * n + u, j * n + v, 0);
            add((j - 1) * n + v, j * n + u, 0);
        }
    }
    dijk();
    int ans = 0x3fffffff;
    for(int i = 1; i <= k + 1; i++)
        ans = min(dist[i * n], ans);
    printf("%d\n", ans);
    return 0;
}
 

T2

P4568 [JLOI2011]飛行路線

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>

using namespace std;
const int N = 1e4 + 5, M = 5e4 + 5, K = 12;
int n, m, k;
int s, t;
struct _edge {
    int Next, v, w;
}e[M * K * 4 + M * 2];
int head[N * K], num;
void add(int from, int to, int dis)
{
    e[++num].Next = head[from];
    e[num].v = to;
    e[num].w = dis;
    head[from] = num;
}
int dist[N * K], vis[N * K];
struct node {
    int u, d;
    bool operator < (const node &x) const {
        return d > x.d;
    }
};
priority_queue<node> q;
void dijk(int x)
{
    memset(dist, 0x3f, sizeof(dist));
    dist[x] = 0;
    q.push((node){x, 0});
    while(!q.empty())
    {
        node tp = q.top(); q.pop();
        int u = tp.u;
        if(u == t + k * n) break;
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = head[u]; i; i = e[i].Next)
        {
            int v = e[i].v, w = e[i].w;
            if(dist[v] > dist[u] + w)
            {
                dist[v] = dist[u] + w;
                if(!vis[v]) q.push((node){v, dist[v]});
            }
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    scanf("%d%d", &s, &t); s++, t++;
    for(int i = 1, u, v, z; i <= m; i++)
    {
        scanf("%d%d%d", &u, &v, &z); u++, v++;
        add(u, v, z); add(v, u, z);
        for(int j = 1; j <= k; j++)
        {
            add(j * n + u, j * n + v, z);
            add(j * n + v, j * n + u, z);
            add((j - 1) * n + u, j * n + v, 0);
            add((j - 1) * n + v, j * n + u, 0);
        }
    }
    dijk(s);
    int ans = 1e9;
    for(int i = 0; i <= k; i++)
        ans = min(ans, dist[t + i * n]);
    printf("%d\n", ans);
    return 0;
}
 

T3

P4822 [BJWC2012]凍結

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;
const int N = 55, M = 1005, K = 55;
int n, m, k;
struct Edge {
    int Next, to, dis;
}e[M * K * 10];
int head[N * K * 10], num;
void add(int from, int to, int dis)
{
    e[++num].Next = head[from];
    e[num].to = to;
    e[num].dis = dis;
    head[from] = num;
}
struct node {
    int u, d;
    bool operator < (const node& x) const {
        return d > x.d;
    } 
};
priority_queue<node> q;
int dist[N * K * 10], vis[N * K * 10];
void dijk()
{
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    q.push((node){1, 0});
    while(!q.empty())
    {
        int u = q.top().u; q.pop();
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = head[u]; i; i = e[i].Next)
        {
            int v = e[i].to, w = e[i].dis;
            if(dist[v] > dist[u] + w)
            {
                dist[v] = dist[u] + w;
                if(!vis[v]) q.push((node){v, dist[v]});
            }
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1, u, v, z; i <= m; i++)
    {
        scanf("%d%d%d", &u, &v, &z);
        add(u, v, z); add(v, u, z);
        for(int j = 1; j <= k; j++)
        {
            add(j * n + u, j * n + v, z);
            add(j * n + v, j * n + u, z);
            add((j - 1) * n + u, j * n + v, z >> 1);
            add((j - 1) * n + v, j * n + u, z >> 1);
        }
    }
    dijk();
    int ans = 0x7fffffff;
    for(int i = 1; i <= k + 1; i++)
        ans = min(ans, dist[i * n]);
    printf("%d\n", ans);
    return 0;
}