視覺化資料是把 資料轉換成視覺或表格的形式，以便可以分析資料和資料項或屬性之間的關係與特性。

視覺化基本步驟：

1.表示

2.安排

3.選擇

視覺化技術：1.直方圖、多維直方圖 2.盒狀圖（通常顯示資料內部的變化）

3.散佈圖矩陣。下面轉載一篇關於介紹散佈矩陣的博文如下（地址http://blog.csdn.net/breeze5428/article/details/25612763）：

因為最近需要用到散佈矩陣做資料分析，因此在此做些關於散佈矩陣的小總結。在多變數概率統計中，散佈矩陣是用來估計多維正態分佈協方差的統計量。

定義

給定n個維的樣本，用矩陣的矩陣表示以上資料，其中。於是可得樣本的均值為

其中 是矩陣的第列.

散佈矩陣為的半正定矩陣

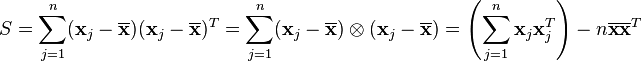
 其中表示矩陣的轉置。散佈矩陣可以簡要的表示為

在此，定義為centering matrix，具體定義為

。

應用

在最大似然估計中， 給定n個樣本，一個多元正太分佈的協方差可以表示為歸一化的散度矩陣：

若中的樣本從多元正態分佈中獨立抽取，則 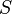  服從Wishart分佈.

與協方差的關係

以上僅是從維基百科上翻譯過來的內容，不難發現散佈矩陣和協方差矩陣的關係。散佈矩陣前乘以係數1/n就可以得到協方差矩陣。如果熟悉PCA，我們就會發現可以利用散度矩陣做PCA。

4.等高線圖：適用於連續屬性是且空間網格測量時。

5.平行座標：用來繪製高維資料的屬性值，採用同一平行軸與垂直軸

OLAP操作：

切片，切塊，向上瀏覽，向下瀏覽