二叉排序樹C++實現
阿新 • • 發佈:2018-12-30
簡介
學習了演算法導論12章關於二叉排序樹的內容,自己利用C++實現了二叉排序樹的封裝。由此對二叉樹這種資料結構理解更加深刻了,對於遞迴在樹中的應用之廣更是有深切體會,例如遞迴建立,遞迴前,中,後序遍歷,返回樹高(個人最喜歡這個樹高遞迴函式,一句話返回樹高確實酷),遞迴刪除等……因為很多樹本身就是遞迴定義的。(刪除某節點比較難,有3,4種情況要分別考慮,暫時沒有實現,後續再補吧)
有什麼不足之處希望不吝賜教!
具體實現
標頭檔案二叉排序樹類的定義
註釋比較清楚,就不再贅述了:
#pragma once
#include<iostream>
using namespace std;
//樹節點定義,包含父節點指標(便於回溯前驅與後繼) 成員函式的實現:
#include "BSearchTree.h"
BSearchTree::BSearchTree(void)
{
root = NULL;
}
BSearchTree::~BSearchTree(void)
{
//to do sth
}
//建立二叉排序樹(匯入陣列內元素,逐一插入)
void BSearchTree:: createBSTree(int *dataset, int size) {
for ( int i=0; i<size; i++ ) {
insertNode(&root,dataset[i]);
}
}
//插入新節點
//注意因為要修改root根指標的值,所以需要傳入二級指標
bool BSearchTree:: insertNode(Node_t **root, int value) {
//初始化將插入的新節點
Node_t *new_node = new Node_t;
if ( new_node == NULL ) {
return false;
}
new_node->data = value;
new_node->leftchild = new_node->rightchild = new_node->parent = NULL;
//空樹時,直接讓根指標指向新節點
if( (*root) == NULL ) {
*root = new_node;
return true;
}
//插入到當前結點(*root)的左孩子
if ((*root)->leftchild == NULL && (*root)->data > value ) {
new_node->parent = (*root);
(*root)->leftchild = new_node;
return true;
}
//插入到當前結點(*root)的右孩子
if((*root)->rightchild == NULL && (*root)->data < value){
new_node->parent = (*root);
(*root)->rightchild = new_node;
return true;
}
//遞迴法插入新節點
if ( (*root)->data > value ) { //新節點的值小於根節點,遞迴尋找左邊空位
insertNode( &(*root)->leftchild,value); //關鍵點
}
else if ( (*root)->data < value ) { //新節點的值大於根節點,遞迴尋找右邊空位
insertNode( &(*root)->rightchild,value);
} else {
return true;
}
}
//中序遍歷
void BSearchTree:: inorderTraverse(Node_t *root) const {
//遞迴出口
if ( root == NULL ) {
return;
}
inorderTraverse( root->leftchild );
cout<< root->data <<" ";
inorderTraverse( root->rightchild );
}
void BSearchTree::visitMiddleOrder() const {
inorderTraverse(this->root);
}
//按值查詢,返回節點的地址
Node_t* BSearchTree:: searchNode(Node_t *root,int value) const {
if ( root == NULL ) {
return NULL;
}
if ( root->data > value ) {
searchNode( root->leftchild,value);
}
else if ( root->data < value ) {
searchNode( root->rightchild,value);
} else {
return root;
}
}
void BSearchTree:: searchByValue(int value) const{
Node_t *p_findnode = this->searchNode(root,value);
if ( p_findnode == NULL ) {
cout<<"沒有找到該節點"<<endl;
} else {
cout<< "該節點存在" <<endl;
}
}
//獲取最大值
void BSearchTree:: getMax(Node_t *root) const {
while( root->rightchild ) {
root = root->rightchild;
}
cout<<root->data<<endl;
}
//獲取最小值
void BSearchTree:: getMin(Node_t *root) const {
while( root->leftchild ) {
root = root->leftchild;
}
cout<<root->data<<endl;
}
//獲取節點前驅
void BSearchTree:: getPredecessor(Node_t *node) {
//節點如果有左子樹,則其前驅節點是左子樹的最大值
if ( node->leftchild != NULL ) {
return getMax( node->leftchild );
} else {
cout<<"(該點無左子樹,開始回溯祖先...)"<<endl;
}
//如果沒有右子樹,則向上回溯,最頂層的祖先節點則是後繼
Node_t *y = node->parent; //y首先指向該節點的父節點
while( y != NULL && node == y->leftchild ) {
node = y;
y = y->parent;
}
cout<<y->data;
}
//獲取節點後繼
void BSearchTree:: getSuccessor(Node_t *node) {
//節點如果有右子樹,則其後繼節點是右子樹的最小值
if ( node->rightchild != NULL ) {
return getMin( node->rightchild );
} else {
cout<<"(該點無右子樹,開始回溯祖先...)"<<endl;
}
//如果沒有右子樹,則向上回溯,最頂層的祖先節點則是後繼
Node_t *y = node->parent;
while( y != NULL && node == y->rightchild ) { //遇到第一個“拐角”回溯結束
node = y; //節點向上爬一層
y = y->parent; //y也向上逐層回溯祖先
}
cout<<y->data;
}
//返回樹高,樹通用寫法
//ps:演算法導論認為只有一個根節點時樹高為0,我們常認為1
int BSearchTree::getHeight(Node_t *root) const {
return root ? max(getHeight(root->leftchild),getHeight(root->rightchild))+1 : -1;
}測試程式碼:
#include"BSearchTree.h"
void main(void) {
int arrs[] = { 14,2,4,10,3,5,8,23,18,35 };
//int arrs[] = { 23, 65, 12, 3, 8, 76, 90, 21, 75, 34,345, 61 };
int len = sizeof(arrs) / sizeof(arrs[0]);
BSearchTree bsearch_tree;
bsearch_tree.createBSTree(arrs,len);
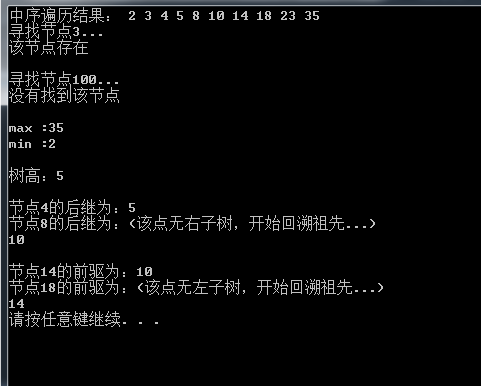
cout<<"中序遍歷結果: ";
bsearch_tree.visitMiddleOrder();
cout<<endl;
cout<<"尋找節點3..."<<endl;
bsearch_tree.searchByValue(3);
cout<<endl;
cout<<"尋找節點100..."<<endl;
bsearch_tree.searchByValue(100);
cout<<endl;
cout<<"max :";
bsearch_tree.getMax(bsearch_tree.getRoot());
cout<<"min :";
bsearch_tree.getMin(bsearch_tree.getRoot());
cout<<endl;
cout<<"樹高:"<< bsearch_tree.getHeight(bsearch_tree.getRoot())<<endl<<endl;
Node_t *pnext = bsearch_tree.searchNode(bsearch_tree.getRoot(),4);
cout<<"節點"<<pnext->data<<"的後繼為:";
bsearch_tree.getSuccessor(bsearch_tree.searchNode(bsearch_tree.getRoot(),4));
pnext = bsearch_tree.searchNode(bsearch_tree.getRoot(),8);
cout<<"節點"<<pnext->data<<"的後繼為:";
bsearch_tree.getSuccessor(bsearch_tree.searchNode(bsearch_tree.getRoot(),8));
cout<<endl;
cout<<endl;
Node_t *pbefore = bsearch_tree.searchNode(bsearch_tree.getRoot(),14);
cout<<"節點"<<pbefore->data<<"的前驅為:";
bsearch_tree.getPredecessor(bsearch_tree.searchNode(bsearch_tree.getRoot(),14));
pbefore = bsearch_tree.searchNode(bsearch_tree.getRoot(),18);
cout<<"節點"<<pbefore->data<<"的前驅為:";
bsearch_tree.getPredecessor(bsearch_tree.searchNode(bsearch_tree.getRoot(),18));
cout<<endl;
system("pause");
}