http://hihocoder.com/contest/hiho56/problem/1

高斯消元就是用多元一次方程求解
小Ho：<吧唧><吧唧><吧唧>

小Hi：小Ho，你還吃呢。想好了麼?

小Ho：腫搶著呢(正想著呢)…<吞嚥>…我記得這個問題上課有提到過，應該是一元一次方程組吧。

我們把每一件商品的價格看作是x[1]…x[n]，第i個組合中第j件商品數量記為a[i][j]，其價格記作y[i]，則可以列出方程式：

我們可以對方程組進行3種操作而不改變方程組的解集：

1. 交換兩行。

2. 把第i行乘以一個非0係數k。即對於j = 1…n， 令a[i][j] = ka[i][j], y[i]=k

   y[i]

3. 把第p行乘以一個非0係數k之後加在第i行上。即對於j=1…n， 令a[i][j] = a[i][j]+ka[p][j]，y[i]=y[i]+kp[i]

以上三個操作叫做初等行變換。

我們可以使用它們，對這個方程組中的a[i][j]進行加減乘除變換，舉個例子：
我們可以通過 式子(1) - 式子(2) * (a[1][1] / a[2][1])，將第1行第1列的a[1][1]變換為0。

對整個方程組進行多次變換之後，可以使得a[i][j]滿足：

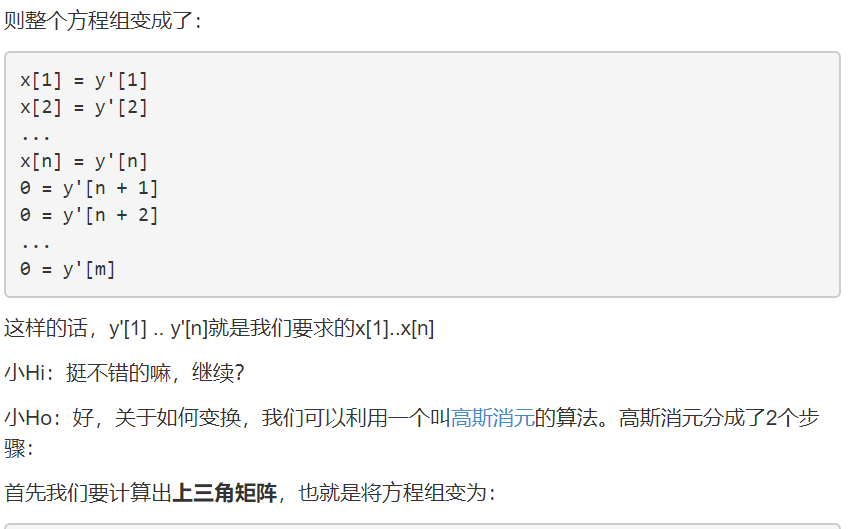
虛擬碼：

// 處理出上三角矩陣
For i = 1..N
    Flag ← False
    For j =
 
 i..M                // 從第i行開始，找到第i列不等於0的行j
        If a[j][i] != 0 Then
            Swap(j, i)          // 交換第i行和第j行
            Flag ← True
            Break
        End If
    End For
    // 若無法找到，則存在多個解
    If (not Flag) Then
        manySolutionsFlag ← True // 出現了秩小於N的情況
        continue;
    End If
    // 消除第i+1行到第M行的第i列
 

    For j = i+1 .. M
        a[j][] ← a[j][] - a[i][] * (a[j][i] / a[i][i])
        b[j] ← b[j] - b[i] * (a[j][i] / a[i][i])
    End For
End For 

// 檢查是否無解，即存在 0 = x 的情況
For i = 1..M
    If (第i行係數均為0 and (b[i] != 0)) Then
        return "No solutions"
    End If
End For

// 判定多解
If (manySolutionsFlag) Then
	return "Many solutions"
End If

// 此時存在唯一解
// 由於每一行都比前一行少一個係數，所以在M行中只有前N行有係數
// 解析來從第N行開始處理每一行的解
For i = N .. 1
    // 利用已經計算出的結果，將第i行中第i+1列至第N列的係數消除
    For j = i + 1 .. N
        b[i] ← b[i] - a[i][j] * value[j]
        a[i][j] ← 0
    End For
    value[i] ← b[i] / a[i][i]
End For

AC程式碼：

注意，用double的大於0的時候，要去一個eps近似值，
還有最後輸出的時候要轉成int（x+0.5)，原因我還不知道，如果有知道的，可以在評論區指出來，感謝^- ^

#include <bits/stdc++.h>

using namespace std;
#define LL long long
const int Mod = 1e9 + 7;
const int maxn = 1e3 + 5;
const double eps = 0.0000001;
const int INF = 0x3f3f3f3f;

int n, m;
double a[maxn][maxn], x[maxn];
bool manySolutionFlag = false, noSolution = false;

void Swap(int i, int j) {
    for (int k = 1; k <= n + 1; k ++)
        swap(a[i][k], a[j][k]);
}

bool Check(int i) {
    bool vis = false;
    for (int j = 1; j <= n; j ++) {
        if(fabs(a[i][j]) >= eps) vis = true;
    }
    if(!vis && fabs(a[i][n + 1]) >= eps) return false;
    return true;
}

void GS() {
    for (int i = 1; i <= n; i ++) {
        bool flag = false;
        for (int j = i; j <= m; j ++) {
            if(a[j][i] != 0) {
                Swap(j, i);
                flag = true;
                break;
            }
        }
        if(!flag) {
            manySolutionFlag = true;
        }
        for (int j = i + 1; j <= m; j ++)
            for (int k = n + 1; k >= i; k --)
                a[j][k] = a[j][k] * 1. - a[i][k] * (a[j][i] * 1./a[i][i] * 1.) * 1.;

    }
    for (int i = 1; i <= m; i ++) {
        if(!Check(i)) {
            noSolution = true;
            return ;
        }
    }
    for (int i = n; i >= 1; i --) {
        for (int j = i + 1; j <= n; j ++) {
            a[i][n + 1] = a[i][n + 1] - a[i][j] * x[j];
            a[i][j] = 0;
        }
        x[i] = a[i][n + 1] * 1./a[i][i] * 1.;
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i ++)
        for (int j = 1; j <= n + 1; j ++)
            cin >> a[i][j];
    GS();
    if(noSolution) cout << "No solutions" << endl;
    else if(manySolutionFlag) cout << "Many solutions" << endl;
    else {
        for (int i = 1; i <= n; i ++)
            cout << (int)(x[i] +0.5) << endl;
    }
    return 0;
}