hihor學習日記:hiho一下 第五十五週 (點的雙連通分量)
阿新 • • 發佈:2018-12-30
http://hihocoder.com/contest/hiho55/problem/1
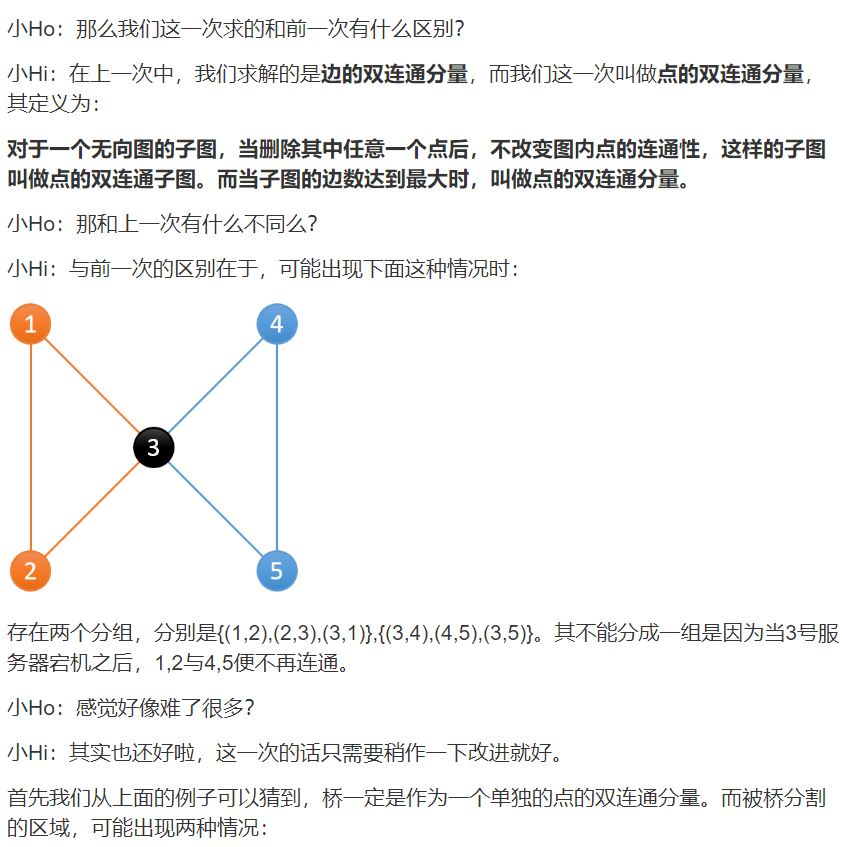
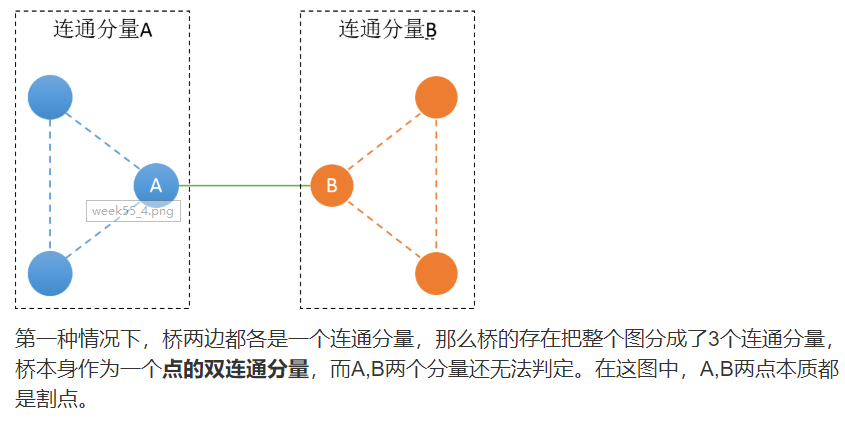
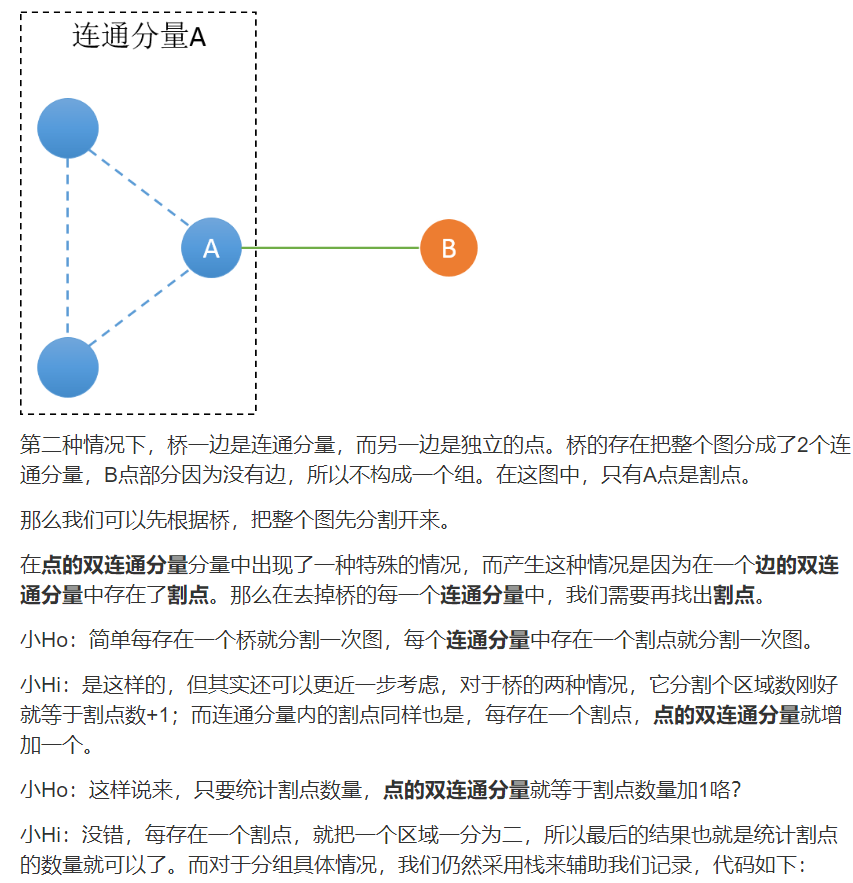
與邊的雙聯通分量類似,這個是求的割點
虛擬碼:
void dfs(int u) {
//記錄dfs遍歷次序
static int counter = 0;
//記錄節點u的子樹數
int children = 0;
ArcNode *p = graph[u].firstArc;
visit[u] = 1;
//初始化dfn與low
dfn[u] = low[u] = ++counter;
for(; p != NULL; p = p->next) {
int v = AC程式碼:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int Mod = 1e9 + 7;
const int maxn = 2e5 + 5;
const double eps = 0.00000001;
const int INF = 0x3f3f3f3f;
struct Edge{
int u, v, nxt, id;
}edge[maxn << 1];
int tot, top, head[maxn];
int dfn[maxn], low[maxn], belong[maxn], par[maxn], Stack[maxn], Min[maxn];
int n, m, cnt;
void init() {
cnt = top = tot = 0;
memset(head, -1, sizeof(head));
memset(belong, -1, sizeof(belong));
memset(par, -1, sizeof(par));
memset(Min, INF, sizeof(Min));
memset(dfn, 0, sizeof(dfn));
}
void addEdge(int u, int v, int id) {
edge[tot].u = u;
edge[tot].v = v;
edge[tot].nxt = head[u];
edge[tot].id = id;
head[u] = tot ++;
edge[tot].u = v;
edge[tot].v = u;
edge[tot].nxt = head[v];
edge[tot].id = id;
head[v] = tot ++;
}
void dfs(int u) {
static int counter = 0;
int child = 0;
low[u] = dfn[u] = ++counter;
for (int i = head[u]; i + 1; i = edge[i].nxt) {
if(belong[edge[i].id] != -1) continue;
int v = edge[i].v;
if(!dfn[v]) {
child ++;
par[v] = u;
Stack[++ top] = edge[i].id;
dfs(v);
low[u] = min(low[v], low[u]);
if((par[u] == -1 && child > 1) || (par[u] != -1 && low[v] >= dfn[u])) {
cnt ++;
int minn = INF;
do{
belong[Stack[top]] = cnt;
minn = min(minn, Stack[top]);
}while(Stack[top--] != edge[i].id);
Min[cnt] = minn;
}
}else if(par[u] != v) {
Stack[++ top] = edge[i].id;
low[u] = min(low[u], dfn[v]);
}
}
}
int main()
{
init();
cin >> n >> m;
for (int i = 1; i <= m; i ++) {
int u, v;
cin >> u >> v;
addEdge(u, v, i);
}
dfs(1);
cnt ++;
int minn = INF;
while(top != 0) {
belong[Stack[top]] = cnt;
minn = min(minn, Stack[top]);
top --;
}
Min[cnt] = minn;
cout << cnt << endl;
for (int i = 1; i <= m; i ++) {
cout << Min[belong[i]] << " ";
}
return 0;
}
