文章目錄

• 時間複雜度
• 空間複雜度
• 二分查詢
• 氣泡排序
• 選擇排序
• 插入排序
• 快速排序
• 歸併排序
• 計數排序

時間複雜度

時間複雜度是用來估算演算法執行效率的描述，不可精確定量計算，一般用O(n)表示。

#程式碼片1
print("Hello World!")	#時間複雜度O(1)
#程式碼片2
for i in range(n):		#時間複雜度O(n)
	print("Hello World!")
#程式碼片3
for i in range(n):		#時間複雜度O(n*n)
	for j in range(n):
		print("Hello World!")
#程式碼片4
for i in range(n):		#時間複雜度O(n*n*n)
	for j in range(n):
		for j in range(n):
			print("Hello World!")
#程式碼片5
 

while n > 1:			
	print(n)
	n = n // 2

• 程式碼片1時間複雜度O(1)
• 程式碼片2時間複雜度O(n)
• 程式碼片3時間複雜度O(n²)
• 程式碼片4時間複雜度O(n³)
• 程式碼片4時間複雜度O(log₂n)可以簡寫為O(logn)
  小結：
• 時間複雜度是用來估算演算法執行時間的一個單位
• 一般來說，時間複雜度越高的演算法比複雜度低的演算法慢，效率低
• 常見的時間複雜度安效率排序：O(1) > O(logn) > O(n) > O(nlogn) > O(n²) > O(n²logn) > O(n³
  )

空間複雜度

空間複雜度用來評估演算法對記憶體佔用的估算單位。為了提高演算法的執行效率，降低時間複雜度，經常使用一空間換時間的演算法。
未使用額外空間的演算法空間複雜度為O(1)；
使用額外空間的演算法空間複雜度為O(n)

二分查詢

# 此演算法的前提是data_list是一個按升序排列的列表
# 迴圈版本的二分查詢
def bin_search(data_list, value):
	low = 0
	high = len(data_list) - 1
	while low <= high :
		mid = (low + high) // 2
		if data_list[mid] == value:
			return mid
		elif data_list[mid] > value:
			high = mid -1
		else:
			low = mid + 1
# 遞迴版本的二分查詢
def bin_search_rec(data_list, vaule, low, high):
	if low <= high:
		mid = (low + high) // 2
		if data_list[mid] == value:
			return mid
		elif data_list[mid] > value:
			return bin_search_rec(data_list, vaule, low, mid -1)
		else:
			return bin_search_rec(data_list, vaule, mid + 1, high)
	else:
		return None

氣泡排序

時間複雜度: O(n²)
空間複雜度:O(1)

def bubble_sort(data_list):
	for i in range(len(data_list) - 1):
		for j in range(len(li) - i - 1):
			if data_list[j] > data_list[j + 1]:
				data_list[j], data_list[j+1] = data_list[j+1], data_list[j]

# 氣泡排序優化， 如果執行一趟比較，沒有發生交換，則列表已經是有序狀態，可以直接結束演算法
def bubble_sort_2(data_list):
	for i in range(len(data_list) - 1):
		exchange = False
		for j in range(len(li) - i - 1):
			if data_list[j] > data_list[j + 1]:
				data_list[j], data_list[j+1] = data_list[j+1], data_list[j]
				exchange = True
		if not exchange:
			return

選擇排序

思路：初始時認為最小的元素位於0，然後遍歷列表與元素0比較，找出最小元素的位置，然後交換，然後依次比較剩餘區的最小元素，進行交換。
時間複雜度: O(n²)
空間複雜度:O(1)

def select_sort(data_list):
	for i in range(len(data_list) - 1):
		min_location = i
		for j in range(i+1, len(data_list)):
			if data_list[j] < data_list[min_location]:
				min_location = j
		if min_location != i:
			data_list[i], data_list[min_location ] = data_list[min_location ], data_list[i]

插入排序

思路：列表被分為有序區與無序區，最初有序區只有一個元素，即為第0個元素，依次從無序區拿出一個元素，與有序區比較，將元素插入到有序區相應的位置，直到無序區沒有元素，排序完成
時間複雜度: O(n²)
空間複雜度:O(1)

def insert_sort(data_list):
	for i in range(1, len(data_list)):
		tmp = data_list[i]	#從無序區拿出的第一個元素
		j = i - 1
		while j >= 0 and tmp < data_list[j]:
			data_list[j + 1] = data_list[j]
			j = j - 1
		data_list[j + 1] = tmp	

快速排序

快速排序思路：

• 取第一個元素p， 使p元素歸位
• 所謂歸位，是指將p元素移動到一個位置，此位置的右邊元素都比p大，左邊都比p小
• 歸位後的返回值為p元素歸位後的位置
• 然後根據此位置遞迴完成左邊與右邊的元素的歸位
• • 時間複雜度：O(nlogn)
• 空間複雜度：O(1)

# partition函式首先從left位置取出一個元素p，暫存到tmp，
# 然後從right位置開始比較，當right元素比tmp小時，將此right元素移動到left位置，否則right-1；
# 然後再從left位置開始與tmp比較，當left元素比tmp大時，將left元素移動到right位置，否則left+1
# 最後當left與right相等時，使tmp元素歸位，即可保證元素右邊比p大，左邊比p小
def partition(data, left, right):
	tmp = data[left]
	while left < right:
		while left < right and data[right] >= tmp:
			right -= 1
		data[left] = data[right]
		while left < right and data[left] <= tmp:
			left += 1
		data[right] = data[left]
	data[left] = tmp
	return left
def quick_sort(data, left, right):
	if left < right:
		mid = partition(data, left, right)
		quick_sort(data, left, mid-1)
		quick_sort(data, mid+1, right)

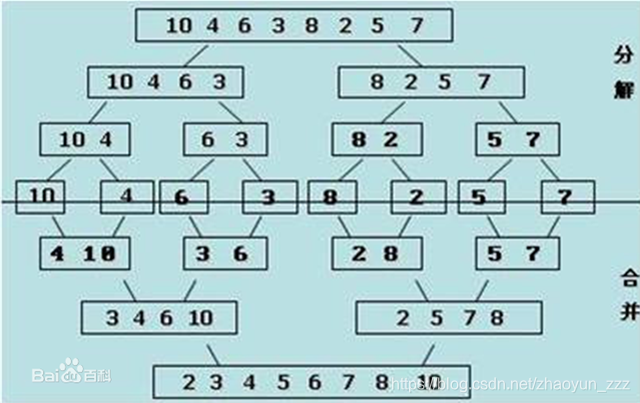
歸併排序

歸併排序思路：

• 分解，首先將列表分解，直至分解成單個元素
• 單個元素永遠是有序的
• 合併，將兩個有序的列表合併，
• 時間複雜度：O(nlogn)
• 空間複雜度：O(n)
  

def merge(data, low, mid, high):
	i = low
	j = mid + 1
	Ltmp = []
	while i <= mid and j <= high:
		if data[i] <= data[j]:
			Ltmp.append(data[i])
			i += 1
		else:
			Ltmp.append(data[j])
			j += 1
	while i <= mid:
		Ltmp.append(data[i])
		i += 1
	while j <= high:
		Ltmp.append(data[j])
		j += 1
	data[left:high+1 ] = Ltmp
def merge_sort(data, low, high):
	if low < high:
		mid = (low + high) // 2
		merge_sort(data, low, mid)
		merge_sort(data, mid+1, high)
		merge(data, low, mid, high)

計數排序

計數排序思路：

• 首先建立一個以待排序列表中最大值為元素個數的計數列表，
• 列表每個元素的初始值均為0
• 然後統計待排序列表中的元素， 以元素的值為下標，每出現一次；在計數列表中次數加1
• 然後根據計數列表中不為0的元素，按照下標順序以及次數，將下標放置到新的排序列表，排序完成
• 時間複雜度：O(n)
• 空間複雜度：O(n)

def count_sort(data_list, max_value):
	count = [0 for i in range(max_value + 1)]
	for data in data_list:
		count[data] += 1
	i = 0
	for num, v in enumerate(count):
		for j in range(v):
			data_list[i] = num
			i += 1

我是頭一次見到計數排序這種思路，讓我大開眼界。
好了，關於排序的演算法節寫這麼多，以後還要總結一下關於資料結構方面的知識。