霍夫變換——直線檢測
霍夫變換(Hough)通過轉換座標系,將特定形狀的檢測對映到引數空間中,從而根據引數空間中的值來確定特定形狀的相關資訊。
Hough變換的比較簡單的應用例子有檢測直線。
檢測直線
設空間中有若干點,我們要判斷這些點是否能構成一條直線,即為直線檢測。平面中直線的通用公式為xcos(θ)+ysin(θ)=ρxcos(θ)+ysin(θ)=ρ。常用的y=wx+by=wx+b公式,因為不能相容y=by=b的情況,所以不能使用。對於某個點,其座標是(xi,yi)(xi,yi),過該點的直線有無數條,這些直線統一表示為xicos(θ)+yisin(θ)=ρxicos(θ)+yisin(θ)=ρ,其中xi,yixi,yi是常量。反過來看,代表這些直線的公式,可以看做θθ為自變數,ρρ為因變數,xi,yixi,yi為常量引數的直線公式。這樣,在x-y空間過(xi,yi)(xi,yi)的無數條直線,可以在θ−ρθ−ρ空間中用一條線代表。見下圖:
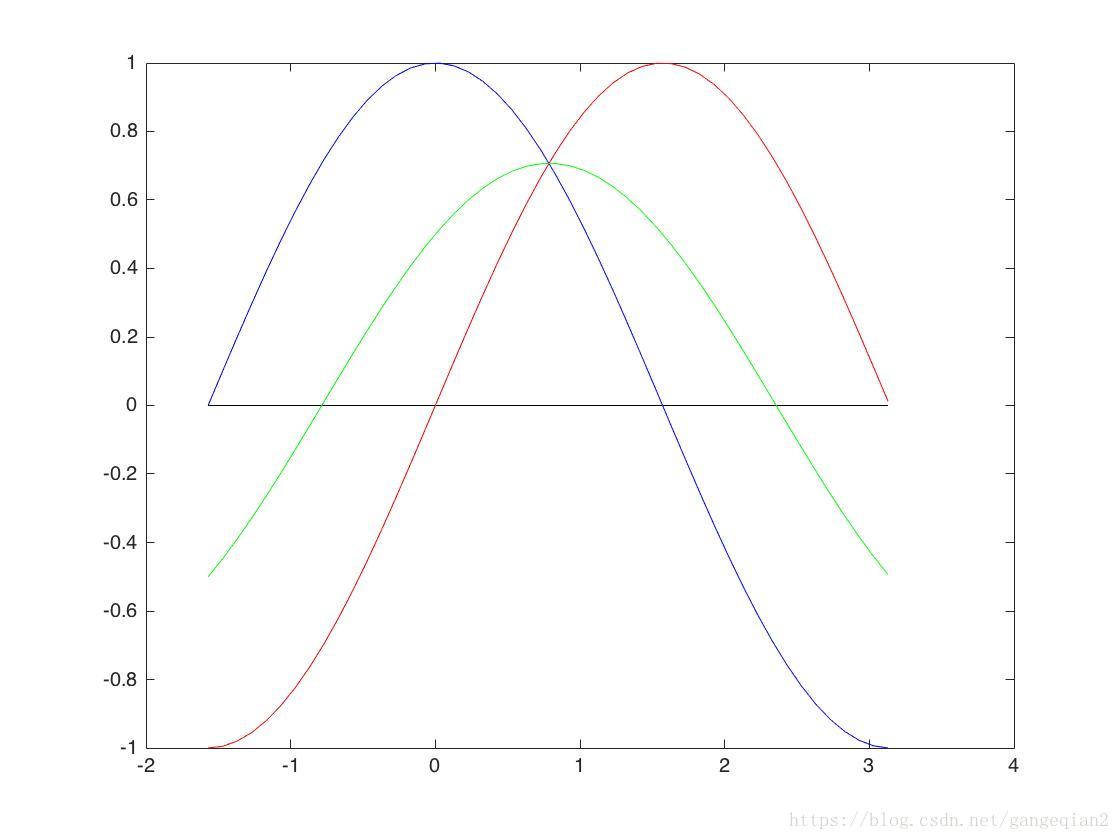
上圖是x-y空間,下圖是θ−ρθ−ρ空間。其中紅、綠、藍三條線可以匯聚成一個點,說明這三條線對應的點,其在θ−ρθ−ρ空間中的直線引數是一樣的。反過來就是說,穿過這三個點的無數直線中,有“三”條直線,其θ,ρθ,ρ值相同,這“三“條直線是一根直線,即這三個點可以共線。
通過量化霍夫引數空間為有限個值間隔等分或者累加格子。當霍夫變換演算法開始,每個畫素
座標點P(x, y)被轉換到(r, theta)的曲線點上面,累加到對應的格子資料點,當一個波峰出現
時候,說明有直線存在。
程式設計思路解析:
讀取一幅帶處理二值影象,最好背景為黑色。
取得源畫素資料
根據直線的霍夫變換公式完成霍夫變換,預覽霍夫空間結果
尋找最大霍夫值,設定閾值,反變換到影象RGB值空間(程式難點之一)
越界處理,顯示霍夫變換處理以後的影象
對於0~70°範圍內直線檢測結果:


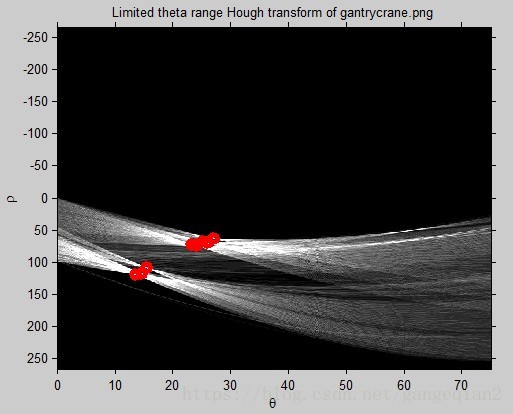

-70~0°範圍內直線檢測:

matlab程式碼:
%% 霍夫曼變換 檢測直線
clear all;
close all;
% I=imread('gantrycrane.png');
I=imread('3.jpg');
Ihsv=rgb2hsv(I);
Iv=Ihsv(:,:,3