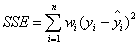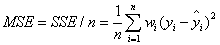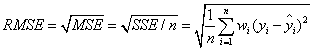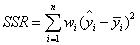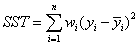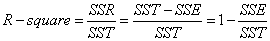該統計引數計算的是擬合數據和原始資料對應點的誤差的平方和，計算公式如下

SSE越接近於0，說明模型選擇和擬合更好，資料預測也越成功。接下來的MSE和RMSE因為和SSE是同出一宗，所以效果一樣


二、MSE(均方差)
該統計引數是預測資料和原始資料對應點誤差的平方和的均值，也就是SSE/n，和SSE沒有太大的區別，計算公式如下

三、RMSE(均方根)
該統計引數，也叫回歸系統的擬合標準差，是MSE的平方根，就算公式如下

在這之前，我們所有的誤差引數都是基於預測值(y_hat)和原始值(y)之間的誤差(即點對點)。從下面開始是所有的誤差都是相對原始資料平均值(y_ba)而展開的(即點對全)!!!


四、R-square(確定係數)
在講確定係數之前，我們需要介紹另外兩個引數SSR和SST，因為確定係數就是由它們兩個決定的
(1)SSR：Sum of squares of the regression，即預測資料與原始資料均值之差的平方和，公式如下

(2)SST：Total sum of squares，即原始資料和均值之差的平方和，公式如下

細心的網友會發現，SST=SSE+SSR，呵呵只是一個有趣的問題。而我們的“確定係數”是定義為SSR和SST的比值，故

其實“確定係數”是通過資料的變化來表徵一個擬合的好壞。由上面的表示式可以知道“確定係數”的正常取值範圍為[0 1]，越接近1，表明方程的變數對y的解釋能力越強，這個模型對資料擬合的也較好