Tensorflow一些常用函式
阿新 • • 發佈:2018-12-31
1、tensorflow的基本運作
為了快速的熟悉TensorFlow程式設計,下面從一段簡單的程式碼開始:
import tensorflow as tf
#定義‘符號’變數,也稱為佔位符
a = tf.placeholder("float")
b = tf.placeholder("float")
y = tf.mul(a, b) #構造一個op節點
sess = tf.Session()#建立會話
#執行會話,輸入資料,並計算節點,同時列印結果
print sess.run(y, feed_dict={a: 3, b: 3})
# 任務完成, 關閉會話.
sess.close() - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
其中tf.mul(a, b)函式便是tf的一個基本的算數運算,接下來介紹跟多的相關函式。
2、tf函式
TensorFlow 將圖形定義轉換成分散式執行的操作, 以充分利用可用的計算資源(如 CPU 或 GPU。一般你不需要顯式指定使用 CPU 還是 GPU, TensorFlow 能自動檢測。如果檢測到 GPU, TensorFlow 會盡可能地利用找到的第一個 GPU 來執行操作.
平行計算能讓代價大的演算法計算加速執行,TensorFlow也在實現上對複雜操作進行了有效的改進。大部分核相關的操作都是裝置相關的實現,比如GPU。下面是一些重要的操作/核:
- 1
- 2
- 3
| 操作組 | 操作 |
|---|---|
| Maths | Add, Sub, Mul, Div, Exp, Log, Greater, Less, Equal |
| Array | Concat, Slice, Split, Constant, Rank, Shape, Shuffle |
| Matrix | MatMul, MatrixInverse, MatrixDeterminant |
| Neuronal Network | SoftMax, Sigmoid, ReLU, Convolution2D, MaxPool |
| Checkpointing | Save, Restore |
| Queues and syncronizations | Enqueue, Dequeue, MutexAcquire, MutexRelease |
| Flow control | Merge, Switch, Enter, Leave, NextIteration |
TensorFlow的算術操作如下:
| 操作 | 描述 |
|---|---|
| tf.add(x, y, name=None) | 求和 |
| tf.sub(x, y, name=None) | 減法 |
| tf.mul(x, y, name=None) | 乘法 |
| tf.div(x, y, name=None) | 除法 |
| tf.mod(x, y, name=None) | 取模 |
| tf.abs(x, name=None) | 求絕對值 |
| tf.neg(x, name=None) | 取負 (y = -x). |
| tf.sign(x, name=None) | 返回符號 y = sign(x) = -1 if x < 0; 0 if x == 0; 1 if x > 0. |
| tf.inv(x, name=None) | 取反 |
| tf.square(x, name=None) | 計算平方 (y = x * x = x^2). |
| tf.round(x, name=None) | 舍入最接近的整數 # ‘a’ is [0.9, 2.5, 2.3, -4.4] tf.round(a) ==> [ 1.0, 3.0, 2.0, -4.0 ] |
| tf.sqrt(x, name=None) | 開根號 (y = \sqrt{x} = x^{1/2}). |
| tf.pow(x, y, name=None) | 冪次方 # tensor ‘x’ is [[2, 2], [3, 3]] # tensor ‘y’ is [[8, 16], [2, 3]] tf.pow(x, y) ==> [[256, 65536], [9, 27]] |
| tf.exp(x, name=None) | 計算e的次方 |
| tf.log(x, name=None) | 計算log,一個輸入計算e的ln,兩輸入以第二輸入為底 |
| tf.maximum(x, y, name=None) | 返回最大值 (x > y ? x : y) |
| tf.minimum(x, y, name=None) | 返回最小值 (x < y ? x : y) |
| tf.cos(x, name=None) | 三角函式cosine |
| tf.sin(x, name=None) | 三角函式sine |
| tf.tan(x, name=None) | 三角函式tan |
| tf.atan(x, name=None) | 三角函式ctan |
張量操作Tensor Transformations
- 資料型別轉換Casting
| 操作 | 描述 |
|---|---|
| tf.string_to_number (string_tensor, out_type=None, name=None) | 字串轉為數字 |
| tf.to_double(x, name=’ToDouble’) | 轉為64位浮點型別–float64 |
| tf.to_float(x, name=’ToFloat’) | 轉為32位浮點型別–float32 |
| tf.to_int32(x, name=’ToInt32’) | 轉為32位整型–int32 |
| tf.to_int64(x, name=’ToInt64’) | 轉為64位整型–int64 |
| tf.cast(x, dtype, name=None) | 將x或者x.values轉換為dtype # tensor a is [1.8, 2.2], dtype=tf.floattf.cast(a, tf.int32) ==> [1, 2] # dtype=tf.int32 |
- 形狀操作Shapes and Shaping
| 操作 | 描述 |
|---|---|
| tf.shape(input, name=None) | 返回資料的shape # ‘t’ is [[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]] shape(t) ==> [2, 2, 3] |
| tf.size(input, name=None) | 返回資料的元素數量 # ‘t’ is [[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]]] size(t) ==> 12 |
| tf.rank(input, name=None) | 返回tensor的rank 注意:此rank不同於矩陣的rank, tensor的rank表示一個tensor需要的索引數目來唯一表示任何一個元素 也就是通常所說的 “order”, “degree”或”ndims” #’t’ is [[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]] # shape of tensor ‘t’ is [2, 2, 3] rank(t) ==> 3 |
| tf.reshape(tensor, shape, name=None) | 改變tensor的形狀 # tensor ‘t’ is [1, 2, 3, 4, 5, 6, 7, 8, 9] # tensor ‘t’ has shape [9] reshape(t, [3, 3]) ==> [[1, 2, 3], [4, 5, 6], [7, 8, 9]] #如果shape有元素[-1],表示在該維度打平至一維 # -1 將自動推導得為 9: reshape(t, [2, -1]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3], [4, 4, 4, 5, 5, 5, 6, 6, 6]] |
| tf.expand_dims(input, dim, name=None) | 插入維度1進入一個tensor中 #該操作要求-1-input.dims() # ‘t’ is a tensor of shape [2] shape(expand_dims(t, 0)) ==> [1, 2] shape(expand_dims(t, 1)) ==> [2, 1] shape(expand_dims(t, -1)) ==> [2, 1] <= dim <= input.dims() |
- 切片與合併(Slicing and Joining)
| 操作 | 描述 |
|---|---|
| tf.slice(input_, begin, size, name=None) | 對tensor進行切片操作 其中size[i] = input.dim_size(i) - begin[i] 該操作要求 0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n] #’input’ is #[[[1, 1, 1], [2, 2, 2]],[[3, 3, 3], [4, 4, 4]],[[5, 5, 5], [6, 6, 6]]] tf.slice(input, [1, 0, 0], [1, 1, 3]) ==> [[[3, 3, 3]]] tf.slice(input, [1, 0, 0], [1, 2, 3]) ==> [[[3, 3, 3], [4, 4, 4]]] tf.slice(input, [1, 0, 0], [2, 1, 3]) ==> [[[3, 3, 3]], [[5, 5, 5]]] |
| tf.split(split_dim, num_split, value, name=’split’) | 沿著某一維度將tensor分離為num_split tensors # ‘value’ is a tensor with shape [5, 30] # Split ‘value’ into 3 tensors along dimension 1 split0, split1, split2 = tf.split(1, 3, value) tf.shape(split0) ==> [5, 10] |
| tf.concat(concat_dim, values, name=’concat’) | 沿著某一維度連結tensor t1 = [[1, 2, 3], [4, 5, 6]] t2 = [[7, 8, 9], [10, 11, 12]] tf.concat(0, [t1, t2]) ==> [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]] tf.concat(1, [t1, t2]) ==> [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]] 如果想沿著tensor一新軸連結打包,那麼可以: tf.concat(axis, [tf.expand_dims(t, axis) for t in tensors]) 等同於tf.pack(tensors, axis=axis) |
| tf.pack(values, axis=0, name=’pack’) | 將一系列rank-R的tensor打包為一個rank-(R+1)的tensor # ‘x’ is [1, 4], ‘y’ is [2, 5], ‘z’ is [3, 6] pack([x, y, z]) => [[1, 4], [2, 5], [3, 6]] # 沿著第一維pack pack([x, y, z], axis=1) => [[1, 2, 3], [4, 5, 6]] 等價於tf.pack([x, y, z]) = np.asarray([x, y, z]) |
| tf.reverse(tensor, dims, name=None) | 沿著某維度進行序列反轉 其中dim為列表,元素為bool型,size等於rank(tensor) # tensor ‘t’ is [[[[ 0, 1, 2, 3], #[ 4, 5, 6, 7], #[ 8, 9, 10, 11]], #[[12, 13, 14, 15], #[16, 17, 18, 19], #[20, 21, 22, 23]]]] # tensor ‘t’ shape is [1, 2, 3, 4] # ‘dims’ is [False, False, False, True] reverse(t, dims) ==> [[[[ 3, 2, 1, 0], [ 7, 6, 5, 4], [ 11, 10, 9, 8]], [[15, 14, 13, 12], [19, 18, 17, 16], [23, 22, 21, 20]]]] |
| tf.transpose(a, perm=None, name=’transpose’) | 調換tensor的維度順序 按照列表perm的維度排列調換tensor順序, 如為定義,則perm為(n-1…0) # ‘x’ is [[1 2 3],[4 5 6]] tf.transpose(x) ==> [[1 4], [2 5],[3 6]] # Equivalently tf.transpose(x, perm=[1, 0]) ==> [[1 4],[2 5], [3 6]] |
| tf.gather(params, indices, validate_indices=None, name=None) | 合併索引indices所指示params中的切片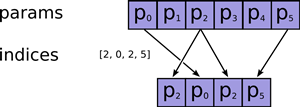 |
| tf.one_hot (indices, depth, on_value=None, off_value=None, axis=None, dtype=None, name=None) | indices = [0, 2, -1, 1] depth = 3 on_value = 5.0 off_value = 0.0 axis = -1 #Then output is [4 x 3]: output = [5.0 0.0 0.0] // one_hot(0) [0.0 0.0 5.0] // one_hot(2) [0.0 0.0 0.0] // one_hot(-1) [0.0 5.0 0.0] // one_hot(1) |
矩陣相關運算
| 操作 | 描述 |
|---|---|
| tf.diag(diagonal, name=None) | 返回一個給定對角值的對角tensor # ‘diagonal’ is [1, 2, 3, 4] tf.diag(diagonal) ==> [[1, 0, 0, 0] [0, 2, 0, 0] [0, 0, 3, 0] [0, 0, 0, 4]] |
| tf.diag_part(input, name=None) | 功能與上面相反 |
| tf.trace(x, name=None) | 求一個2維tensor足跡,即對角值diagonal之和 |
| tf.transpose(a, perm=None, name=’transpose’) | 調換tensor的維度順序 按照列表perm的維度排列調換tensor順序, 如為定義,則perm為(n-1…0) # ‘x’ is [[1 2 3],[4 5 6]] tf.transpose(x) ==> [[1 4], [2 5],[3 6]] # Equivalently tf.transpose(x, perm=[1, 0]) ==> [[1 4],[2 5], [3 6]] |
| tf.matmul(a, b, transpose_a=False, transpose_b=False, a_is_sparse=False, b_is_sparse=False, name=None) | 矩陣相乘 |
| tf.matrix_determinant(input, name=None) | 返回方陣的行列式 |
| tf.matrix_inverse(input, adjoint=None, name=None) | 求方陣的逆矩陣,adjoint為True時,計算輸入共軛矩陣的逆矩陣 |
| tf.cholesky(input, name=None) | 對輸入方陣cholesky分解, 即把一個對稱正定的矩陣表示成一個下三角矩陣L和其轉置的乘積的分解A=LL^T |
| tf.matrix_solve(matrix, rhs, adjoint=None, name=None) | 求解tf.matrix_solve(matrix, rhs, adjoint=None, name=None) matrix為方陣shape為[M,M],rhs的shape為[M,K],output為[M,K] |
複數操作
| 操作 | 描述 |
|---|---|
| tf.complex(real, imag, name=None) | 將兩實數轉換為複數形式 # tensor ‘real’ is [2.25, 3.25] # tensor imag is [4.75, 5.75]tf.complex(real, imag) ==> [[2.25 + 4.75j], [3.25 + 5.75j]] |
| tf.complex_abs(x, name=None) | 計算複數的絕對值,即長度。 # tensor ‘x’ is [[-2.25 + 4.75j], [-3.25 + 5.75j]] tf.complex_abs(x) ==> [5.25594902, 6.60492229] |
| tf.conj(input, name=None) | 計算共軛複數 |
| tf.imag(input, name=None) tf.real(input, name=None) | 提取複數的虛部和實部 |
| tf.fft(input, name=None) | 計算一維的離散傅立葉變換,輸入資料型別為complex64 |
歸約計算(Reduction)
| 操作 | 描述 |
|---|---|
| tf.reduce_sum(input_tensor, reduction_indices=None, keep_dims=False, name=None) | 計算輸入tensor元素的和,或者安照reduction_indices指定的軸進行求和 # ‘x’ is [[1, 1, 1] # [1, 1, 1]] tf.reduce_sum(x) ==> 6 tf.reduce_sum(x, 0) ==> [2, 2, 2] tf.reduce_sum(x, 1) ==> [3, 3] tf.reduce_sum(x, 1, keep_dims=True) ==> [[3], [3]] tf.reduce_sum(x, [0, 1]) ==> 6 |
| tf.reduce_prod(input_tensor, reduction_indices=None, keep_dims=False, name=None) | 計算輸入tensor元素的乘積,或者安照reduction_indices指定的軸進行求乘積 |
| tf.reduce_min(input_tensor, reduction_indices=None, keep_dims=False, name=None) | 求tensor中最小值 |
| tf.reduce_max(input_tensor, reduction_indices=None, keep_dims=False, name=None) | 求tensor中最大值 |
| tf.reduce_mean(input_tensor, reduction_indices=None, keep_dims=False, name=None) | 求tensor中平均值 |
| tf.reduce_all(input_tensor, reduction_indices=None, keep_dims=False, name=None) | 對tensor中各個元素求邏輯’與’ # ‘x’ is # [[True, True] # [False, False]] tf.reduce_all(x) ==> False tf.reduce_all(x, 0) ==> [False, False] tf.reduce_all(x, 1) ==> [True, False] |
| tf.reduce_any(input_tensor, reduction_indices=None, keep_dims=False, name=None) | 對tensor中各個元素求邏輯’或’ |
| tf.accumulate_n(inputs, shape=None, tensor_dtype=None, name=None) | 計算一系列tensor的和 # tensor ‘a’ is [[1, 2], [3, 4]] # tensor b is [[5, 0], [0, 6]]tf.accumulate_n([a, b, a]) ==> [[7, 4], [6, 14]] |
| tf.cumsum(x, axis=0, exclusive=False, reverse=False, name=None) | 求累積和 tf.cumsum([a, b, c]) ==> [a, a + b, a + b + c] tf.cumsum([a, b, c], exclusive=True) ==> [0, a, a + b] tf.cumsum([a, b, c], reverse=True) ==> [a + b + c, b + c, c] tf.cumsum([a, b, c], exclusive=True, reverse=True) ==> [b + c, c, 0] |
分割(Segmentation)
| 操作 | 描述 |
|---|---|
| tf.segment_sum(data, segment_ids, name=None) | 根據segment_ids的分段計算各個片段的和 其中segment_ids為一個size與data第一維相同的tensor 其中id為int型資料,最大id不大於size c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) tf.segment_sum(c, tf.constant([0, 0, 1])) ==>[[0 0 0 0] [5 6 7 8]] 上面例子分為[0,1]兩id,對相同id的data相應資料進行求和, 並放入結果的相應id中, 且segment_ids只升不降 |
| tf.segment_prod(data, segment_ids, name=None) | 根據segment_ids的分段計算各個片段的積 |
| tf.segment_min(data, segment_ids, name=None) | 根據segment_ids的分段計算各個片段的最小值 |
| tf.segment_max(data, segment_ids, name=None) | 根據segment_ids的分段計算各個片段的最大值 |
| tf.segment_mean(data, segment_ids, name=None) | 根據segment_ids的分段計算各個片段的平均值 |
| tf.unsorted_segment_sum(data, segment_ids, num_segments, name=None) | 與tf.segment_sum函式類似, 不同在於segment_ids中id順序可以是無序的 |
| tf.sparse_segment_sum(data, indices, segment_ids, name=None) | 輸入進行稀疏分割求和 c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment. tf.sparse_segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0])) ==> [[0 0 0 0]] 對原data的indices為[0,1]位置的進行分割, 並按照segment_ids的分組進行求和 |
序列比較與索引提取(Sequence Comparison and Indexing)
| 操作 | 描述 |
|---|---|
| tf.argmin(input, dimension, name=None) | 返回input最小值的索引index |
| tf.argmax(input, dimension, name=None) | 返回input最大值的索引index |
| tf.listdiff(x, y, name=None) | 返回x,y中不同值的索引 |
| tf.where(input, name=None) | 返回bool型tensor中為True的位置 # ‘input’ tensor is #[[True, False] #[True, False]] # ‘input’ 有兩個’True’,那麼輸出兩個座標值. # ‘input’的rank為2, 所以每個座標為具有兩個維度. where(input) ==> [[0, 0], [1, 0]] |
| tf.unique(x, name=None) | 返回一個元組tuple(y,idx),y為x的列表的唯一化資料列表, idx為x資料對應y元素的index # tensor ‘x’ is [1, 1, 2, 4, 4, 4, 7, 8, 8] y, idx = unique(x) y ==> [1, 2, 4, 7, 8] idx ==> [0, 0, 1, 2, 2, 2, 3, 4, 4] |
| tf.invert_permutation(x, name=None) | 置換x資料與索引的關係 # tensor x is [3, 4, 0, 2, 1]invert_permutation(x) ==> [2, 4, 3, 0, 1] |
神經網路(Neural Network)
- 啟用函式(Activation Functions)
| 操作 | 描述 |
|---|---|
| tf.nn.relu(features, name=None) | 整流函式:max(features, 0) |
| tf.nn.relu6(features, name=None) | 以6為閾值的整流函式:min(max(features, 0), 6) |
| tf.nn.elu(features, name=None) | |
| tf.nn.softplus(features, name=None) | 計算softplus:log(exp(features) + 1) |
| tf.nn.dropout(x, keep_prob, noise_shape=None, seed=None, name=None) | 計算dropout,keep_prob為keep概率 noise_shape為噪聲的shape |
| tf.nn.bias_add(value, bias, data_format=None, name=None) | 對value加一偏置量 此函式為tf.add的特殊情況,bias僅為一維, 函式通過廣播機制進行與value求和, 資料格式可以與value不同,返回為與value相同格式 |
| tf.sigmoid(x, name=None) | y = 1 / (1 + exp(-x)) |
| tf.tanh(x, name=None) | 雙曲線切線啟用函式 |
- 卷積函式(Convolution)
| 操作 | 描述 |
|---|---|
| tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None) | 在給定的4D input與 filter下計算2D卷積 輸入shape為 [batch, height, width, in_channels] |
| tf.nn.conv3d(input, filter, strides, padding, name=None) | 在給定的5D input與 filter下計算3D卷積 輸入shape為[batch, in_depth, in_height, in_width, in_channels] |
- 池化函式(Pooling)
| 操作 | 描述 |
|---|---|
| tf.nn.avg_pool(value, ksize, strides, padding, data_format=’NHWC’, name=None) | 平均方式池化 |
| tf.nn.max_pool(value, ksize, strides, padding, data_format=’NHWC’, name=None) | 最大值方法池化 |
| tf.nn.max_pool_with_argmax(input, ksize, strides, padding, Targmax=None, name=None) | 返回一個二維元組(output,argmax),最大值pooling,返回最大值及其相應的索引 |
| tf.nn.avg_pool3d(input, ksize, strides, padding, name=None) | 3D平均值pooling |
| tf.nn.max_pool3d(input, ksize, strides, padding, name=None) | 3D最大值pooling |
- 資料標準化(Normalization)
| 操作 | 描述 |
|---|---|
| tf.nn.l2_normalize(x, dim, epsilon=1e-12, name=None) | 對維度dim進行L2正規化標準化 output = x / sqrt(max(sum(x**2), epsilon)) |
| tf.nn.sufficient_statistics(x, axes, shift=None, keep_dims=False, name=None) | 計算與均值和方差有關的完全統計量 返回4維元組,*元素個數,*元素總和,*元素的平方和,*shift結果 參見演算法介紹 |
| tf.nn.normalize_moments(counts, mean_ss, variance_ss, shift, name=None) | 基於完全統計量計算均值和方差 |
| tf.nn.moments(x, axes, shift=None, name=None, keep_dims=False) | 直接計算均值與方差 |
- 損失函式(Losses)
| 操作 | 描述 |
|---|---|
| tf.nn.l2_loss(t, name=None) | output = sum(t ** 2) / 2 |
- 分類函式(Classification)
| 操作 | 描述 |
|---|---|
| tf.nn.sigmoid_cross_entropy_with_logits (logits, targets, name=None)* | 計算輸入logits, targets的交叉熵 |
| tf.nn.softmax(logits, name=None) | 計算softmax softmax[i, j] = exp(logits[i, j]) / sum_j(exp(logits[i, j])) |
| tf.nn.log_softmax(logits, name=None) | logsoftmax[i, j] = logits[i, j] - log(sum(exp(logits[i]))) |
| tf.nn.softmax_cross_entropy_with_logits (logits, labels, name=None) | 計算logits和labels的softmax交叉熵 logits, labels必須為相同的shape與資料型別 |
| tf.nn.sparse_softmax_cross_entropy_with_logits (logits, labels, name=None) | 計算logits和labels的softmax交叉熵 |
| tf.nn.weighted_cross_entropy_with_logits (logits, targets, pos_weight, name=None) | 與sigmoid_cross_entropy_with_logits()相似, 但給正向樣本損失加了權重pos_weight |
- 符號嵌入(Embeddings)
| 操作 | 描述 |
|---|---|
| tf.nn.embedding_lookup (params, ids, partition_strategy=’mod’, name=None, validate_indices=True) | 根據索引ids查詢embedding列表params中的tensor值 如果len(params) > 1,id將會安照partition_strategy策略進行分割 1、如果partition_strategy為”mod”, id所分配到的位置為p = id % len(params) 比如有13個ids,分為5個位置,那麼分配方案為: [[0, 5, 10], [1, 6, 11], [2, 7, 12], [3, 8], [4, 9]] 2、如果partition_strategy為”div”,那麼分配方案為: [[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 10], [11, 12]] |
| tf.nn.embedding_lookup_sparse(params, sp_ids, sp_weights, partition_strategy=’mod’, name=None, combiner=’mean’) | 對給定的ids和權重查詢embedding 1、sp_ids為一個N x M的稀疏tensor, N為batch大小,M為任意,資料型別int64 2、sp_weights的shape與sp_ids的稀疏tensor權重, 浮點型別,若為None,則權重為全’1’ |
- 迴圈神經網路(Recurrent Neural Networks)
| 操作 | 描述 |
|---|---|
| tf.nn.rnn(cell, inputs, initial_state=None, dtype=None, sequence_length=None, scope=None) | 基於RNNCell類的例項cell建立迴圈神經網路 |
| tf.nn.dynamic_rnn(cell, inputs, sequence_length=None, initial_state=None, dtype=None, parallel_iterations=None, swap_memory=False, time_major=False, scope=None) | 基於RNNCell類的例項cell建立動態迴圈神經網路 與一般rnn不同的是,該函式會根據輸入動態展開 返回(outputs,state) |
| tf.nn.state_saving_rnn(cell, inputs, state_saver, state_name, sequence_length=None, scope=None) | 可儲存除錯狀態的RNN網路 |
| tf.nn.bidirectional_rnn(cell_fw, cell_bw, inputs, initial_state_fw=None, initial_state_bw=None, dtype=None, sequence_length=None, scope=None) | 雙向RNN, 返回一個3元組tuple (outputs, output_state_fw, output_state_bw) |
— tf.nn.rnn簡要介紹—
cell: 一個RNNCell例項
inputs: 一個shape為[batch_size, input_size]的tensor
initial_state: 為RNN的state設定初值,可選
sequence_length:制定輸入的每一個序列的長度,size為[batch_size],值範圍為[0, T)的int型資料
其中T為輸入資料序列的長度
@
@針對輸入batch中序列長度不同,所設定的動態計算機制
@對於在時間t,和batch的b行,有
(output, state)(b, t) = ? (zeros(cell.output_size), states(b, sequence_length(b) - 1)) : cell(input(b, t), state(b, t - 1))
- 求值網路(Evaluation)
| 操作 | 描述 |
|---|---|
| tf.nn.top_k(input, k=1, sorted=True, name=None) | 返回前k大的值及其對應的索引 |
| tf.nn.in_top_k(predictions, targets, k, name=None) | 返回判斷是否targets索引的predictions相應的值 是否在在predictions前k個位置中, 返回資料型別為bool型別,len與predictions同 |
對於有巨大量的多分類與多標籤模型,如果使用全連線softmax將會佔用大量的時間與空間資源,所以採用候選取樣方法僅使用一小部分類別與標籤作為監督以加速訓練。
| 操作 | 描述 |
|---|---|
| Sampled Loss Functions | |
| tf.nn.nce_loss(weights, biases, inputs, labels, num_sampled, num_classes, num_true=1, sampled_values=None, remove_accidental_hits=False, partition_strategy=’mod’, name=’nce_loss’) | 返回noise-contrastive的訓練損失結果 |
| tf.nn.sampled_softmax_loss(weights, biases, inputs, labels, num_sampled, num_classes, num_true=1, sampled_values=None, remove_accidental_hits=True, partition_strategy=’mod’, name=’sampled_softmax_loss’) | |
| Candidate Samplers | |
| tf.nn.uniform_candidate_sampler(true_classes, num_true, num_sampled, unique, range_max, seed=None, name=None) | 通過均勻分佈的取樣集合 返回三元tuple 1、sampled_candidates 候選集合。 2、期望的true_classes個數,為浮點值 3、期望的sampled_candidates個數,為浮點值 |
| tf.nn.log_uniform_candidate_sampler(true_classes, num_true, num_sampled, unique, range_max, seed=None, name=None) | 通過log均勻分佈的取樣集合,返回三元tuple |
| tf.nn.learned_unigram_candidate_sampler (true_classes, num_true, num_sampled, unique, range_max, seed=None, name=None) | 根據在訓練過程中學習到的分佈狀況進行取樣 返回三元tuple |
| tf.nn.fixed_unigram_candidate_sampler(true_classes, num_true, num_sampled, unique, range_max, vocab_file=”, distortion=1.0, num_reserved_ids=0, num_shards=1, shard=0, unigrams=(), seed=None, name=None) | 基於所提供的基本分佈進行取樣 |
儲存與恢復變數
| 操作 | 描述 |
|---|---|
| 類tf.train.Saver(Saving and Restoring Variables) | |
| tf.train.Saver.__init__(var_list=None, reshape=False, sharded=False, max_to_keep=5, keep_checkpoint_every_n_hours=10000.0, name=None, restore_sequentially=False, saver_def=None, builder=None) | 建立一個儲存器Saver var_list定義需要儲存和恢復的變數 |
| tf.train.Saver.save(sess, save_path, global_step=None, latest_filename=None, meta_graph_suffix=’meta’, write_meta_graph=True) | 儲存變數 |
| tf.train.Saver.restore(sess, save_path) | 恢復變數 |
| tf.train.Saver.last_checkpoints | 列出最近未刪除的checkpoint 檔名 |
| tf.train.Saver.set_last_checkpoints(last_checkpoints) | 設定checkpoint檔名列表 |
| tf.train.Saver.set_last_checkpoints_with_time(last_checkpoints_with_time) | 設定checkpoint檔名列表和時間戳 |
原文:http://blog.csdn.net/lenbow/article/details/52152766
