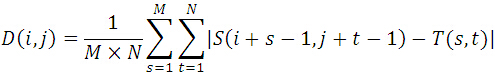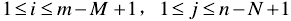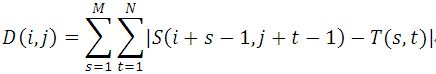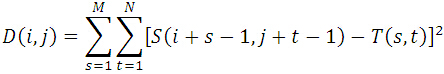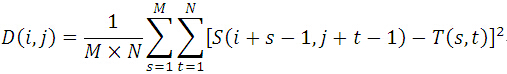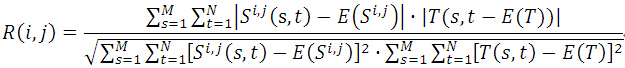簡介：

       本文主要介紹幾種基於灰度的影象匹配演算法：平均絕對差演算法（MAD）、絕對誤差和演算法（SAD）、誤差平方和演算法（SSD）、平均誤差平方和演算法（MSD）、歸一化積相關演算法（NCC）、序貫相似性演算法（SSDA）。下面依次對其進行講解。

MAD演算法

介紹

        平均絕對差演算法（Mean Absolute Differences，簡稱MAD演算法），它是Leese在1971年提出的一種匹配演算法。是模式識別中常用方法，該演算法的思想簡單，具有較高的匹配精度和較少的計算量，廣泛用於影象匹配。

設S(x,y)是大小為mxn的搜尋影象，T(x,y)時MxN的模板影象，分別下圖(a)

演算法思路

        在搜尋圖S中，取以(i,j)為左上角，MxN大小的子圖，計算其與模板圖相似度；在所有能夠取到的子圖中，找到與模板圖最相似的子圖作為最終結果。MAD演算法的相似性測度公式如下。顯然，平均絕對差D(i,j)越小，表明越相似，故只需找到最小的D(i,j)即可確定子圖位置：

其中：

演算法評價：

優點：

①思路簡單，容易理解（子圖與模板圖對應位置上，灰度值之差的絕對值總和，再求平均，實質：是計算的是子圖與模板圖的L1距離的平均值）。

②運算過程簡單，匹配精度高。

缺點：

①運算量偏大。

②對噪聲非常敏感。

——————————————————————————————————————————————————————————————————————————————

SAD演算法

介紹

        絕對誤差和演算法（Sum of Absolute Differences，簡稱SAD演算法）。實際上，SAD演算法與MAD演算法思想幾乎是完全一致，只是其相似度測量公式有一點改動（計算的是子圖與模板圖的L1距離）。這裡不再贅述。

演算法實現

由於文章所介紹的幾個演算法非常相似，所以本文僅列出對SAD演算法進行的程式碼，其餘演算法實現就如出一轍了。

MATLAB程式碼

1. <pre name="code"class="cpp">%%  
2. %絕對誤差和演算法（SAD）  
3. clear all;  
4. close all;  
5. %%  
6. src=imread('lena.jpg'
   );  
7. [a b d]=size(src);  
8. if d==3  
9.     src=rgb2gray(src);  
10. end  
11. mask=imread('lena_mask.jpg');  
12. [m n d]=size(mask);  
13. if d==3  
14.     mask=rgb2gray(mask);  
15. end  
16. %%  
17. N=n;%模板尺寸，預設模板為正方形  
18. M=a;%代搜尋影象尺寸，預設搜尋影象為正方形  
19. %%  
20. dst=zeros(M-N,M-N);  
21. for i=1:M-N         %行  
22.     for j=1:M-N  
23.         temp=src(i:i+N-1,j:j+N-1);  
24.         dst(i,j)=dst(i,j)+sum(sum(abs(temp-mask)));  
25.     end  
26. end  
27. abs_min=min(min(dst));  
28. [x,y]=find(dst==abs_min);  
29. figure;  
30. imshow(mask);title('模板');  
31. figure;  
32. imshow(src);  
33. hold on;  
34. rectangle('position',[x,y,N-1,N-1],'edgecolor','r');  
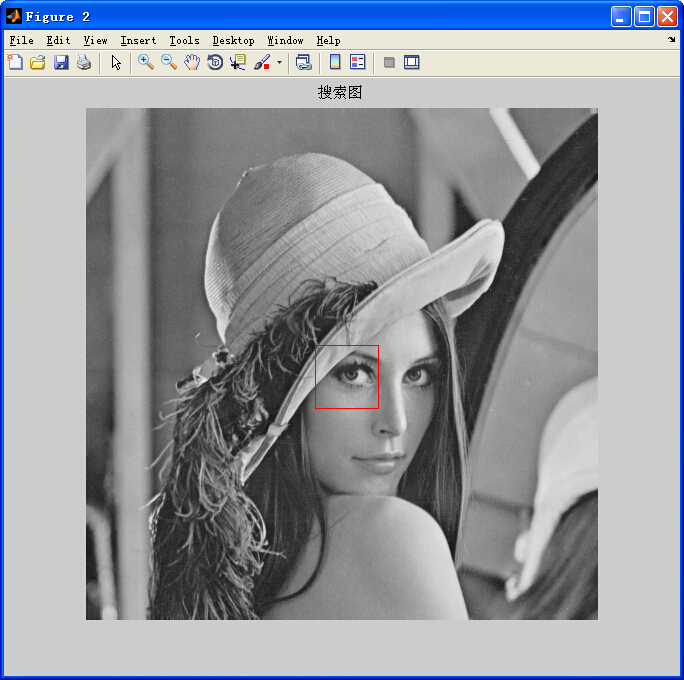
35. hold off;title('搜尋圖');  

輸出結果

——————————————————————————————————————————————————————————————————————————————

SSD演算法

        誤差平方和演算法（Sum of Squared Differences，簡稱SSD演算法），也叫差方和演算法。實際上，SSD演算法與SAD演算法如出一轍，只是其相似度測量公式有一點改動（計算的是子圖與模板圖的L2距離）。這裡不再贅述。

——————————————————————————————————————————————————————————————————————————————

MSD演算法

        平均誤差平方和演算法（Mean Square Differences，簡稱MSD演算法），也稱均方差演算法。實際上，MSD之餘SSD，等同於MAD之餘SAD，故此處不再贅述。

————————————————————————————————————————————————————————————————————————————————

NCC演算法

        歸一化積相關演算法（Normalized Cross Correlation，簡稱NCC演算法），與上面演算法相似，依然是利用子圖與模板圖的灰度，通過歸一化的相關性度量公式來計算二者之間的匹配程度。

其中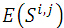，、分別表示(i,j)處子圖、模板的平均灰度值。

OK，以上便是幾種常見的基於灰度的模板匹配演算法。