機器學習中的kNN演算法及Matlab例項
阿新 • • 發佈:2018-12-31
K最近鄰(k-Nearest Neighbor,KNN)分類演算法,是一個理論上比較成熟的方法,也是最簡單的機器學習演算法之一。該方法的思路是:如果一個樣本在特徵空間中的k個最相似(即特徵空間中最鄰近)的樣本中的大多數屬於某一個類別,則該樣本也屬於這個類別。
儘管kNN演算法的思想比較簡單,但它仍然是一種非常重要的機器學習(或資料探勘)演算法。在2006年12月召開的 IEEE
International Conference on Data Mining (ICDM),與會的各位專家選出了當時的十大資料探勘演算法( top 10 data mining algorithms ),可以參加文獻【1】, K
其他本部落格已經介紹過的且位列十大演算法之中的還包括:
二、在Matlab中利用k
如果手頭有一些資料點(以及它們的特徵向量)構成的資料集,對於一個查詢點,我們該如何高效地從資料集中找到它的最近鄰呢?最通常的方法是基於k-d-tree進行最近鄰搜尋。限於篇幅,本文不會對k-d-tree做過深的討論,對此還不甚瞭解的讀者可以參考http://blog.csdn.net/baimafujinji/article/details/52928203。
KNN演算法不僅可以用於分類,還可以用於迴歸,但主要應用於迴歸,所以下面我們就演示在MATLAB中利用KNN演算法進行資料探勘的基本方法。我們所選用的資料集,仍然是較為常用的費希爾鳶尾花資料集,有關這組資料集的基本情況可以參考http://blog.csdn.net/baimafujinji/article/details/49885481。
首先在Matlab中載入資料,程式碼如下,其中meas( : , 3:4)相當於取出(之前文章中的)Petal.Length和Petal.Width這兩列資料,一共150行,三類鳶尾花每類各50行。
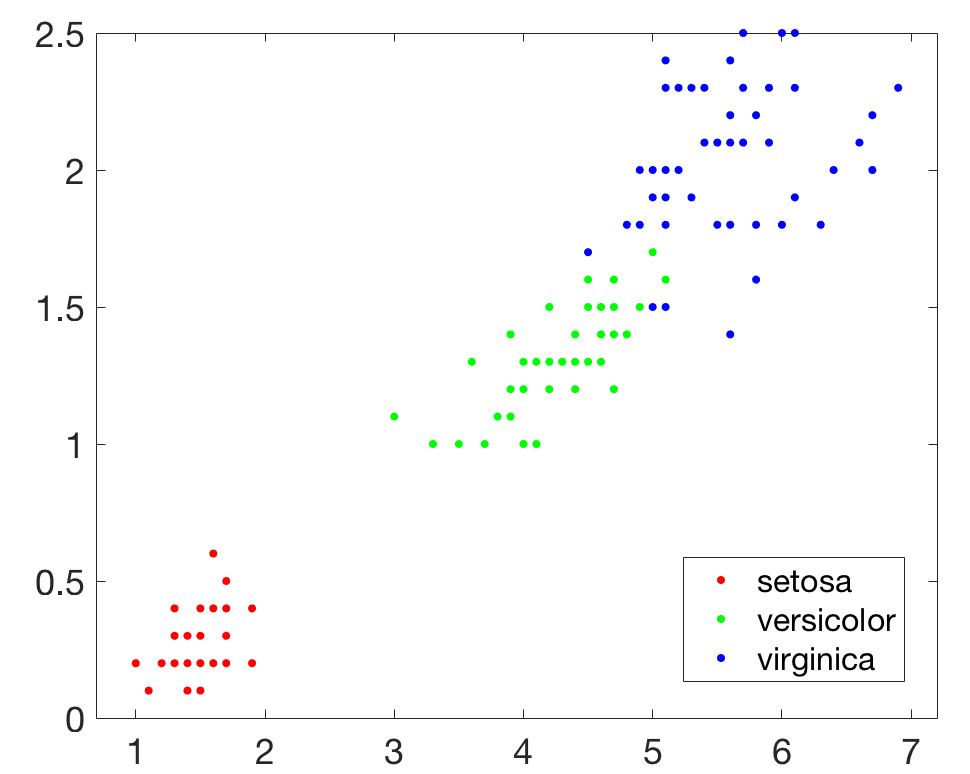
然後我們在引入一個新的查詢點,並在圖上把該點用×標識出來:
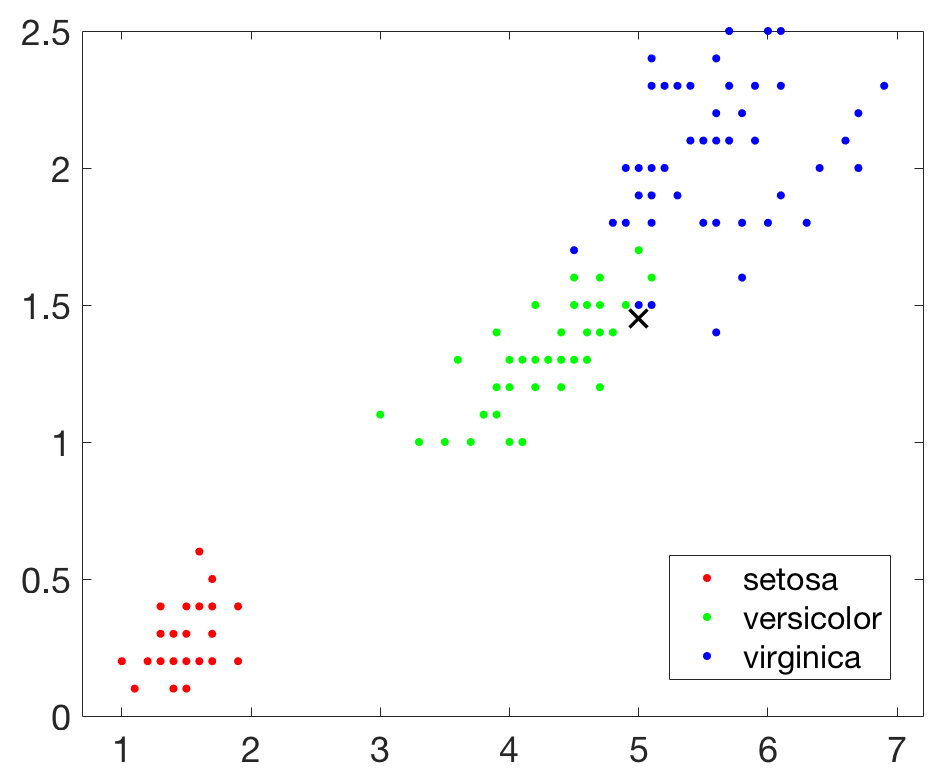
接下來建立一個基於KD-Tree的最近鄰搜尋模型,查詢目標點附近的10個最近鄰居,並在圖中用圓圈標識出來。
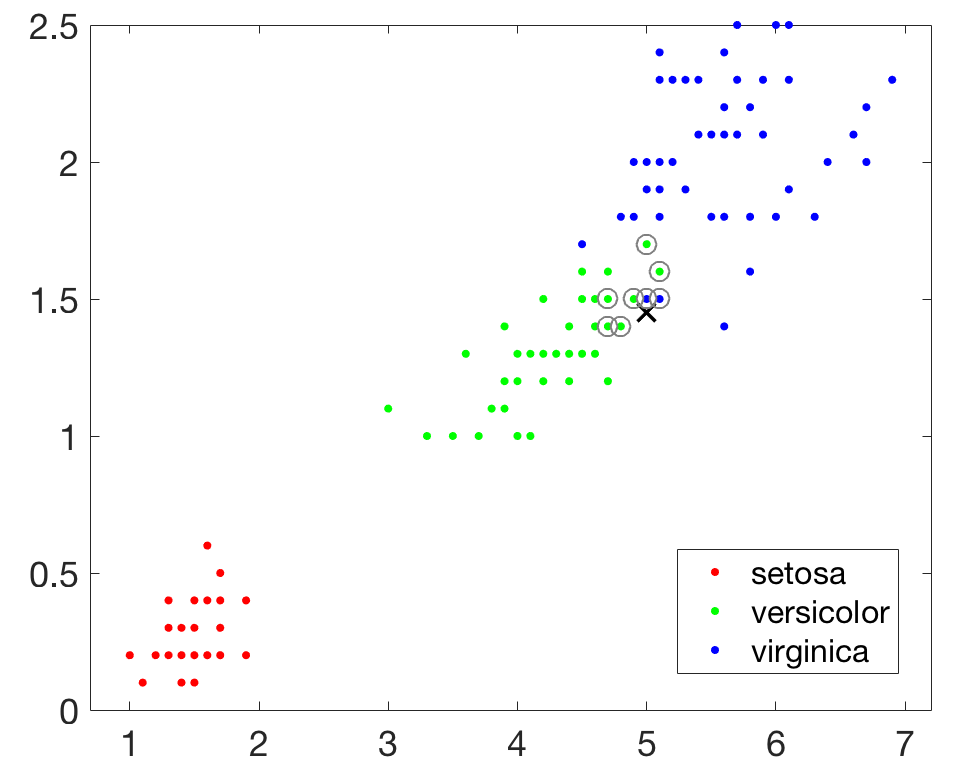
不用著急,其實系統確實找到了10個最近鄰居,但是其中有兩對資料點完全重合,所以在圖上你只能看到8個,不妨把所有資料都輸出來看看,如下所示,可知確實是10個。
在利用 KNN方法進行類別決策時,只與極少量的相鄰樣本有關。由於KNN方法主要靠周圍有限的鄰近的樣本,而不是靠判別類域的方法來確定所屬類別的,因此對於類域的交叉或重疊較多的待分樣本集來說,KNN方法較其他方法更為適合。
我們還要說明在Matlab中使用KDTreeSearcher進行最近鄰搜尋時,距離度量的型別可以是尤拉距離(
三、利用kNN進行資料探勘的例項
下面我們來演示在MATLAB構建kNN分類器,並以此為基礎進行資料探勘的具體步驟。首先還是載入鳶尾花資料,不同的是這次我們使用全部四個特徵來訓練模型。
然後使用fitcknn()函式來訓練分類器模型。
四、關於k值的選擇
kNN演算法在分類時的主要不足在於,當樣本不平衡時,如一個類的樣本容量很大,而其他類樣本容量很小時,有可能導致當輸入一個新樣本時,該樣本的K個鄰居中大容量類的樣本佔多數。因此可以採用權值的方法(和該樣本距離小的鄰居權值大)來改進。
從另外一個角度來說,演算法中k值的選擇對模型本身及其對資料分類的判定結果都會產生重要影響。如果選擇較小的k值,就相當於用較小的領域中的訓練例項來進行預測,學習的近似誤差會減小,只有與輸入例項較為接近(相似的)訓練例項才會對預測結果起作用。但缺點是“學習”的估計誤差會增大。預測結果會對近鄰的例項點非常敏感。如果臨近的例項點恰巧是噪聲,預測就會出現錯誤。換言之,k值的減小意味著整體模型變得複雜,容易發成過擬合。
如果選擇較大的k值,就相當於用較大的鄰域中的訓練例項進行預測,其優點是可以減少學習的估計誤差,但缺點是學習的近似誤差會增大。這時與輸入例項較遠的(不相似的)訓練例項也會對預測起作用,使預測發生錯誤。k值的增大就意味著整體的模型變得簡單。
在應用中,k值一般推薦取一個相對比較小的數值。並可以通過交叉驗證法來幫助選取最優k值。
儘管kNN演算法的思想比較簡單,但它仍然是一種非常重要的機器學習(或資料探勘)演算法。在2006年12月召開的 IEEE
International Conference on Data Mining (ICDM),與會的各位專家選出了當時的十大資料探勘演算法( top 10 data mining algorithms ),可以參加文獻【1】, K
其他本部落格已經介紹過的且位列十大演算法之中的還包括:
- [1] k-means演算法(http://blog.csdn.net/baimafujinji/article/details/50570824)
- [2] 支援向量機SVM(http://blog.csdn.net/baimafujinji/article/details/49885481)
- [3] EM演算法(http://blog.csdn.net/baimafujinji/article/details/50626088)
- [4] 樸素貝葉斯演算法(http://blog.csdn.net/baimafujinji/article/details/50441927)
二、在Matlab中利用k
如果手頭有一些資料點(以及它們的特徵向量)構成的資料集,對於一個查詢點,我們該如何高效地從資料集中找到它的最近鄰呢?最通常的方法是基於k-d-tree進行最近鄰搜尋。限於篇幅,本文不會對k-d-tree做過深的討論,對此還不甚瞭解的讀者可以參考http://blog.csdn.net/baimafujinji/article/details/52928203。
KNN演算法不僅可以用於分類,還可以用於迴歸,但主要應用於迴歸,所以下面我們就演示在MATLAB中利用KNN演算法進行資料探勘的基本方法。我們所選用的資料集,仍然是較為常用的費希爾鳶尾花資料集,有關這組資料集的基本情況可以參考http://blog.csdn.net/baimafujinji/article/details/49885481。
首先在Matlab中載入資料,程式碼如下,其中meas( : , 3:4)相當於取出(之前文章中的)Petal.Length和Petal.Width這兩列資料,一共150行,三類鳶尾花每類各50行。
- load fisheriris
- x = meas(:,3:4);
- gscatter(x(:,1),x(:,2),species)
- legend('Location','best')

然後我們在引入一個新的查詢點,並在圖上把該點用×標識出來:
- newpoint = [5 1.45];
- line(newpoint(1),newpoint(2),'marker','x','color','k',...
- 'markersize',10,'linewidth',2)

接下來建立一個基於KD-Tree的最近鄰搜尋模型,查詢目標點附近的10個最近鄰居,並在圖中用圓圈標識出來。
- >> Mdl = KDTreeSearcher(x)
- Mdl =
- KDTreeSearcher with properties:
- BucketSize: 50
- Distance: 'euclidean'
- DistParameter: []
- X: [150x2 double]
- >> [n,d] = knnsearch(Mdl,newpoint,'k',10);
- line(x(n,1),x(n,2),'color',[.5 .5 .5],'marker','o',...
- 'linestyle','none','markersize',10)

不用著急,其實系統確實找到了10個最近鄰居,但是其中有兩對資料點完全重合,所以在圖上你只能看到8個,不妨把所有資料都輸出來看看,如下所示,可知確實是10個。
- >> x(n,:)
- ans =
- 5.0000 1.5000
- 4.9000 1.5000
- 4.9000 1.5000
- 5.1000 1.5000
- 5.1000 1.6000
- 4.8000 1.4000
- 5.0000 1.7000
- 4.7000 1.4000
- 4.7000 1.4000
- 4.7000 1.5000
- >> tabulate(species(n))
- Value Count Percent
- virginica 2 20.00%
- versicolor 8 80.00%
在利用 KNN方法進行類別決策時,只與極少量的相鄰樣本有關。由於KNN方法主要靠周圍有限的鄰近的樣本,而不是靠判別類域的方法來確定所屬類別的,因此對於類域的交叉或重疊較多的待分樣本集來說,KNN方法較其他方法更為適合。
我們還要說明在Matlab中使用KDTreeSearcher進行最近鄰搜尋時,距離度量的型別可以是尤拉距離(
'euclidean')、曼哈頓距離('cityblock')、閔可夫斯基距離('minkowski')、切比雪夫距離('chebychev'),預設情況下系統使用尤拉距離。你甚至還可以自定義距離函式,然後使用knnsearch()函式來進行最近鄰搜尋,具體可以檢視MATLAB的幫助文件,我們不具體展開。三、利用kNN進行資料探勘的例項
下面我們來演示在MATLAB構建kNN分類器,並以此為基礎進行資料探勘的具體步驟。首先還是載入鳶尾花資料,不同的是這次我們使用全部四個特徵來訓練模型。
- load fisheriris
- X = meas; % Use all data for fitting
- Y = species; % Response data
然後使用fitcknn()函式來訓練分類器模型。
- >> Mdl = fitcknn(X,Y)
- Mdl =
- ClassificationKNN
- ResponseName: 'Y'
- CategoricalPredictors: []
- ClassNames: {'setosa' 'versicolor' 'virginica'}
- ScoreTransform: 'none'
- NumObservations: 150
- Distance: 'euclidean'
- NumNeighbors: 1
- Mdl.NumNeighbors = 4;
- Mdl = fitcknn(X,Y,'NumNeighbors',4);
- >> flwr = [5.0 3.0 5.0 1.45];
- >> flwrClass = predict(Mdl,flwr)
- flwrClass =
- 'versicolor'
- CVMdl = crossval(Mdl);
- >> kloss = kfoldLoss(CVMdl)
- kloss =
- 0.0333
- >> rloss = resubLoss(Mdl)
- rloss =
- 0.0400
四、關於k值的選擇
kNN演算法在分類時的主要不足在於,當樣本不平衡時,如一個類的樣本容量很大,而其他類樣本容量很小時,有可能導致當輸入一個新樣本時,該樣本的K個鄰居中大容量類的樣本佔多數。因此可以採用權值的方法(和該樣本距離小的鄰居權值大)來改進。
從另外一個角度來說,演算法中k值的選擇對模型本身及其對資料分類的判定結果都會產生重要影響。如果選擇較小的k值,就相當於用較小的領域中的訓練例項來進行預測,學習的近似誤差會減小,只有與輸入例項較為接近(相似的)訓練例項才會對預測結果起作用。但缺點是“學習”的估計誤差會增大。預測結果會對近鄰的例項點非常敏感。如果臨近的例項點恰巧是噪聲,預測就會出現錯誤。換言之,k值的減小意味著整體模型變得複雜,容易發成過擬合。
如果選擇較大的k值,就相當於用較大的鄰域中的訓練例項進行預測,其優點是可以減少學習的估計誤差,但缺點是學習的近似誤差會增大。這時與輸入例項較遠的(不相似的)訓練例項也會對預測起作用,使預測發生錯誤。k值的增大就意味著整體的模型變得簡單。
在應用中,k值一般推薦取一個相對比較小的數值。並可以通過交叉驗證法來幫助選取最優k值。
