• Description
  小O和小I一直喜歡打 UOJ 的比賽，然而等了半個丁酉年卻也沒能等到下一次比賽。眼看著 NOI 即將到來，他們決定一探究竟，找出 UOJ 沉寂的真正原因！
  終於有一天，他們得知 UOJ 的管理層全都被兩個一心想摧毀 OI 界的大魔王——滴滴誒柳和不響公座給封印起來。
  這兩個大魔王向來戰略上聯手對敵，戰術上分工合作。每次滴滴誒柳首先給 oier 帶來一堆麻煩；接著不響公座用超聲波對 oier 進行催眠，降低 oier 們的反抗效率；關鍵時候滴滴誒柳又進行反向催眠，讓 oier 拼命反擊筋疲力盡。兩個魔王輪流值班，有著充足的休息時間，而他們的對手卻受到無間斷攻擊。最後隨著時間的推移，oier 們的體力到了最低點時，不響公座放出大招，將 oier 封印起來。
  要想拯救 UOJ，必須打敗這兩個魔王。小O和小I查閱資料，終於找到了獲勝的方法——OI 陣。
  首先，他們需要召集 nn 名 oier 佈陣，聯手對敵。為了高效地反擊滴滴誒柳，他們決定讓 nn 名 oier 站成一張圖的樣子，每個 oier 負責應對自己和相鄰 oier 所受到的攻擊。當一個 oier 受到攻擊時，圖中相鄰的 oier 及時支援。
  同時他們意識到，當一個 oier 身邊有同校的 oier 時，不響公座攻擊的時候他們會聊起天來從而陣法被破；而反之，如果身邊的人都不熟悉，則會產生表現欲，有效抗住不響公座的超聲波攻擊。因此他們要求，圖中任意兩個相鄰的 oier 來自不同的學校。
  現在已知這張圖的構成。該圖具有 nn 個點 mm 條邊，節點編號依次為 1,…,n1,…,n。同時共有 kk 個學校，由於拯救 UOJ 人人有責，故每個學校都有無數的 oier 願意出力。
  小O想要知道有多少種佈陣方式，但是鑑於小I最多隻能數到 55（他學會的最大的數字來自於“一二三四五上山打老虎”），因此小O決定輸出方案數模 6。
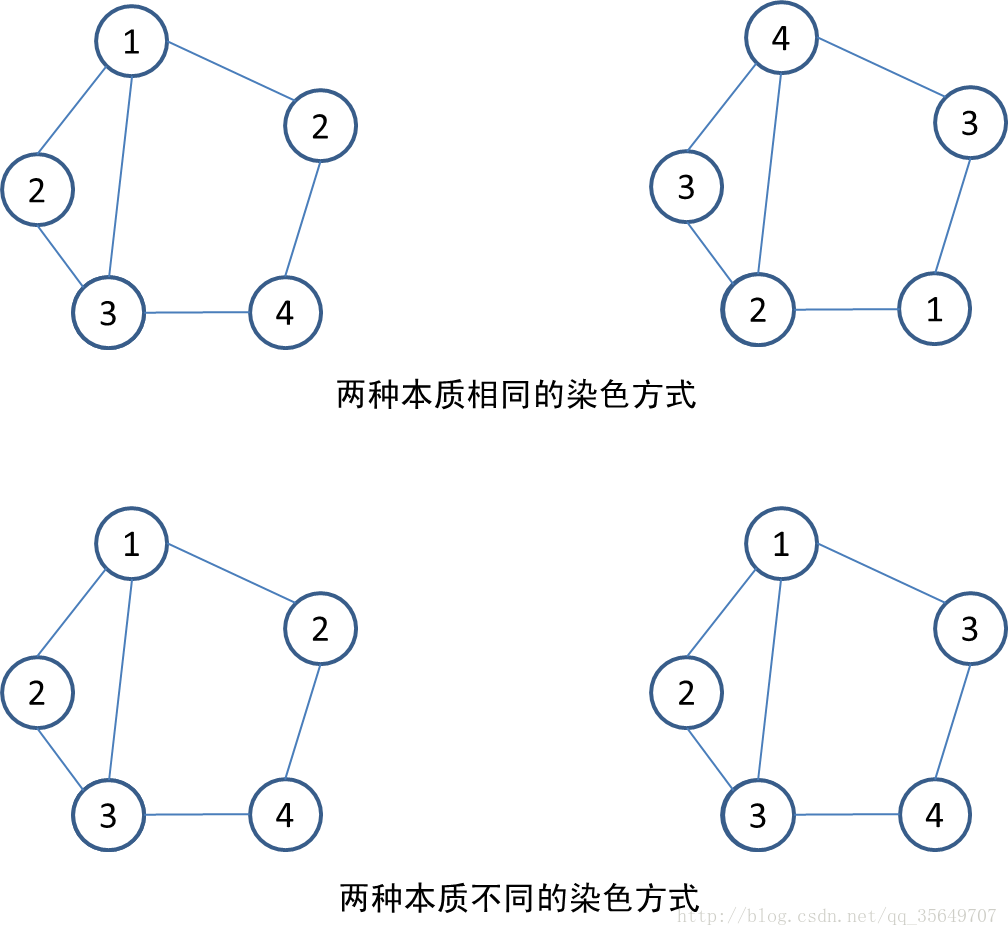
  兩個佈陣方式被認為是不同的當且僅當存在一個節點 ii 使得這兩種佈陣方式中守衛該節點的 oier 來自不同的學校。

• Input
  第一行一個正整數 TT，表示資料組數。
  對於每組資料，第一行三個整數 n,m,kn,m,k，分別表示圖的點數、邊數、總共的學校數。
  接下來 mm行，每行兩個整數 a,ba,b，表示 a,ba,b 間有一條邊。保證 1≤a,b≤n1≤a,b≤n 且 a≠ba≠b。

• Output
  對於每組資料，輸出一個數表示該組資料的答案。

• Sample Input
  2
  5 4 5
  1 2
  1 3
  1 4
  1 5
  8 7 2
  1 2
  2 3
  3 4
  4 5
  5 6
  6 7
  7 8

• Sample Output
  2
  2

• 題解：

其實題意翻譯過來就是給你n個點，m條邊（可能不連通），k種顏色,求使相鄰兩點不同顏色的染色方案數（m

因為有mod6，所以這道題變得簡單了起來。

由題意可得ans=A(k,i)∗i種顏色本質不同的染色方案，所謂本質不同即使指將圖中所有同種顏色的點替換為其他顏色後，兩種染色方式不可能相同。

對於每種染色方式，都可以將四種顏色排列組合，所以ans=A(k,i)∗本質不同的染色方案

對於i≥3,6|A(k,i),所以不予考慮。
對於i=1,如果m≠0則ans=0，否則ans=1
對於i=2,找出圖中聯通塊的個數n，對於固定的兩種顏色，共2n中方式，那麼ans=C(k,2)∗2n
- 注：若m=0則C(k,2)∗(2n−2)。(排除全為一種顏色)。其實可以先處理m等於1的情況，即所有點都獨立，此時a

• Code:

#include<bits/stdc++.h>
using namespace std;
const int Maxn=4e5+60;

inline int read()
{
    char ch=getchar();int i=0,f=1;
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}
    return i*f;
}

int T,n,m,k;
int last[Maxn],before[Maxn],to[Maxn],ecnt,vis[Maxn];

inline void add(int x,int y)
{
    ecnt++;
    before[ecnt]=last[x];
    last[x]=ecnt;
    to[ecnt]=y;
}

inline int power(int x,int y)
{
    int res=1;
    while(y)
    {
        if(y&1)res=((res*x)%6);
        x=(x*x)%6;
        y>>=1;
    }
    return res;
}

inline bool dfs(int i,int col)
{
    vis[i]=col;
    for(int e=last[i];e;e=before[e])
    {
        if(!vis[to[e]]){if(!dfs(to[e],-col))return false;}
        else if(vis[to[e]]==vis[i])return false;
    }
        return true;
}

int main()
{
    T=read();
    while(T--)
    {
        n=read(),m=read(),k=read();
        int ans=0;
        if(m==0)
        {
            cout<<power(k,n)<<endl;
        }
        else
        {
            if(k==1)
            {
                for(int i=1;i<=m;i++)read(),read();
                ans=0;
            }
            else
            {
                memset(vis,0,sizeof(vis));
                memset(last,0,sizeof(last));
                ecnt=0,ans=1;
                int cnt=0;
                int res1=(k*(k-1)/2)%6;
                for(int i=1;i<=m;i++)
                {
                    int x=read(),y=read();
                    add(x,y),add(y,x);
                }
                for(int i=1;i<=n;i++)
                {
                    if(!vis[i])
                    {
                        if(dfs(i,1))++cnt;
                        else
                        {
                            ans=0;break;
                        }
                    }
                }
                ans=(res1*power(2,cnt)*ans%6);
            }
            cout<<ans<<endl;
        }
    }
}