正常卷積運算：

如上圖：4x4的輸入，卷積Kernel為3x3, ,輸出為2x2。其計算可以理解為：
輸入矩陣展開為4*4=16維向量，記作x
輸出矩陣展開為2*2=4維向量，記作y
卷積核C為如下矩陣：

卷積運算可表示為y = Cx（可以對照動圖理解），而卷積的反向傳播可以如下，相當於乘以C^T

反捲積運算：

如上圖：2x2的輸入，卷積Kernel為3x3, ,輸出為4x4。如果按照正常卷積，生成的feature map尺寸應該減小，但是我們現在想要生成尺寸變大，就可以對輸入進行padding。但與正常卷積padding不同的是：反捲積卷積運算的起點不一定在原feature map上，而是從padding區域開始。仔細看上面動圖，可以看到第一個運算卷積核的中點在padding區域上。
反捲積相對於卷積在神經網路結構的正向和反向傳播中做相反的運算。

conv_arithmetic理解：

github連結
上鍊接中的動圖很好解釋了卷積和反捲積的。但由於它把二者分開比較，導致在沒有引數情況下很難理解具體引數意思。首先我們明白在反捲積過程中一定會padding 0的，不然沒辦法擴大輸出map維度。但是這個padding 0卻不叫padding。以下圖為例：

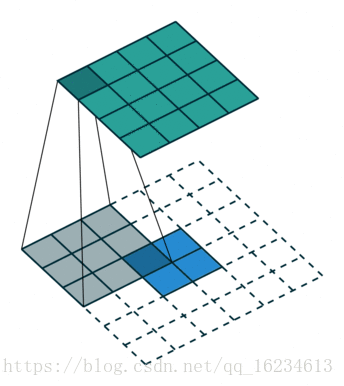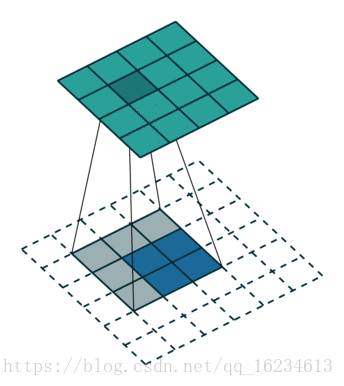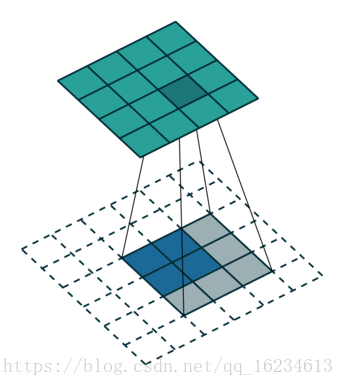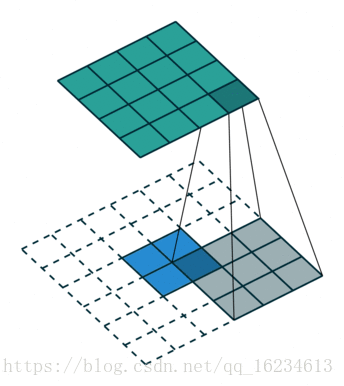
左圖為No padding, no strides；右圖為No padding, no strides, transposed。
明明右圖的反捲積白色區塊填充了0，為啥說是No Padding？這時我們需要看反捲積對應的卷積形式，發現這是因為對應的卷積是No padding的，因此她的反捲積也叫No Padding。同理strides。這時候我們再理解帶strdes的就好理解了：

計算輸出維度：

在理解上面如何計算輸出map的大小呢？此處引用pytorch裡的一個公式和conv_arithmetic中一個動圖為例：


左圖為padding=1, strides=2；右圖為padding=1, strides=2, transposed。
根據上面公式Hin = 3；stride=2；padding=1；kernel_size=3；output_padding=0；
則Hout = （3-1）*2-2*1+3+0=5
總體來說首先根據你要上取樣的大小判斷stride大小，然後根據stride導致的畫素分佈情況確定你的kernel size的視野大小，最後保證-stride+2padding+kernel size=0即可。