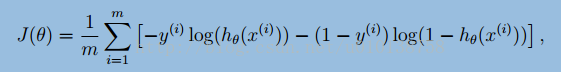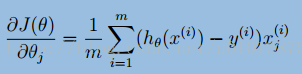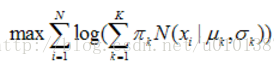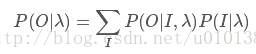最大似然估計、梯度下降、EM演算法、座標上升
機器學習兩個重要的過程:學習得到模型和利用模型進行預測。
下面主要總結對比下這兩個過程中用到的一些方法。
一,求解無約束的目標優化問題
這類問題往往出現在求解模型,即引數學習的階段。
我們已經得到了模型的表示式,不過其中包含了一些未知引數。
我們需要求解引數,使模型在某種性質(目標函式)上最大或最小。
最大似然估計:


其中目標函式是對數似然函式。為了求目標函式取最大值時的theta。
有兩個關機鍵步驟,第一個是對目標函式進行求導,第二個是另導數等於0,求解後直接得到最優theta。兩個步驟缺一不可。
梯度下降:
對目標函式進行求導,利用導函式提供的梯度資訊,使引數往梯度下降最快的方向移動一小步,
來更新引數。為什麼不使用最大似然估計的方法來求解呢?
上面是邏輯迴歸的目標函式,可以看出J(θ)容易進行求導,如下所示:
但是如果通過使偏導數等於0,來求θ是非常困難的。
首先hθ (xi)是關於所有θ的函式,而且h是邏輯迴歸函式,
其次,每個等式中包含m個hθ (xi)函式。因此只能利用梯度資訊,在解空間中進行探索。
EM演算法:
和上面一樣,也是要求優化一個目標函式。
不同的是,它只能得到目標函式,甚至連目標函式的導函式也求不出來。
如下面的高斯混合模型(GMM)的目標函式函式:
對上面的目標函式求導是非常困難的。
在比如下面的隱馬爾科夫模型(HMM)的目標函式:
都是不可以直接求導的,所以需要引入隱變數來簡化計算。
好處是:如果我們知道隱變數的值或者概率分佈,那麼原目標函式可以進行高效的求解(比如可以用最大似然估計法求解)。
通常的步驟是先有引數的先驗值和訓練資料得到隱變數,再由隱變數和訓練資料來最大化目標函式,得到引數。
(個人認為,隱變數可以隨便引入,只要能夠使原目標函式可以高效求解就行。)
座標上升或下降(CoordinateAscent):
由先驗經驗初始化引數。然後每次選擇其中一個引數進行優化,其它引數固定(認為是已知變數),如此進行迭代更新。
它和EM的思想差不多,通過引入隱變數(固定的引數),來使得問題變得高效可解。
而引入的隱變數是通過上一次計算的引數得到的(只不過隱變數就等於部分引數本身而已),相當於引數資訊落後了一代而已。
k-means和高斯混合模型(GMM)中的EM:
k-means是先由引數和資料得到資料的分類標籤,再由資料和分類標籤來計算引數。
高斯混合模型中的EM是先由引數和資料得到資料分類標籤的概率分佈,再由資料和分類標籤分佈來計算引數。
像k-means這樣求隱變數具體值的叫做hard-EM,想GMM這樣求隱變數的概率分佈的叫做soft-EM。
EM演算法收斂性證明:
摘抄自wikipedia中的Expectation–maximization algorithm文章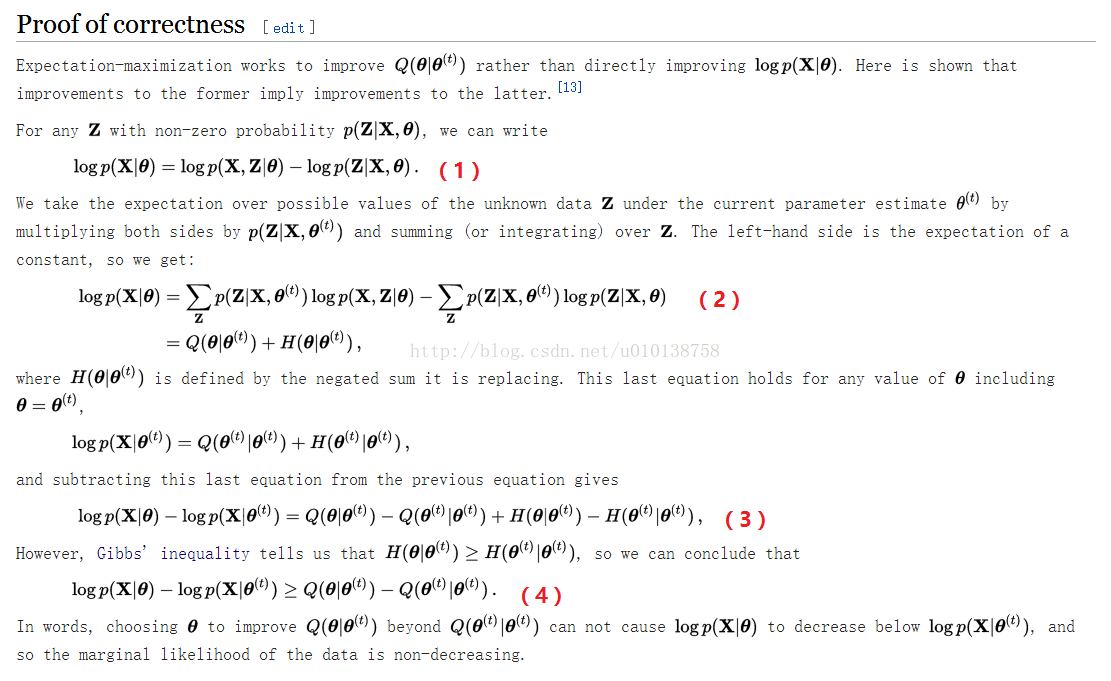
詳細說明:


二,求解有約束的目標優化問題

(之後在總結下,迭代尺度法IIS、 L-BFGS 演算法。以及其其它優化求解方法,前向,後向,維特比,HMM,MaxEnt,CRF的求解優化過程等。) (如果有什麼說的不對的地方,歡迎大家留言指正)