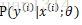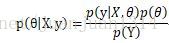最大似然估計、貝葉斯估計、最大後驗估計理論對比
本文要總結的是3種估計的原理、估計與目標函式之間的關係。這三種估計放在一起讓我暈頭轉向了好久,看知乎,看教材,有了以下理解。以下全部是個人看書後的理解,如有理解錯誤的地方,請指正,吾將感激不盡。
來自教材《深度學習》5.4-5.6…
關於頻率派和貝葉斯派:頻率派認為估計的模型是固定的,只是引數θ未知,而資料集樣本是隨機變數。
個人理解,意思是生成真實資料集的概率分佈只有一個,只是我們暫時只能得到從這個分佈中抽取的具體資料,而不知道這個分佈是什麼樣的分佈。認為從分佈中抽取資料是隨機的,因此,將資料樣本看作隨機變數,用這些隨機變數來估計一個最佳最接近真實分佈的引數,引數是資料的函式,並把這個模型分佈當成真實分佈來預測後續隨機變數的概率。
而貝葉斯派認為,資料集能被直接觀測到,那麼它是確定的,不確定的反而是引數,通過確定的樣本來估計引數的條件概率分佈,換言之,引數是資料的條件概率分佈。同時,很重要的一點:貝葉斯估計引入先驗概率,先驗概率是抽樣前有關統計推斷問題的資訊。
最大似然估計(MLE)是頻率派的代表,貝葉斯估計(Bayes)是貝葉斯派的代表,最大後驗估計是頻率派和貝葉斯派的合成。
MLE是點估計,而Bayes是概率估計。
來自知乎最讚的一個回答…
還是有點懵,再理一理公式吧…
1. 最大似然估計(MLE)
最大似然估計的定義
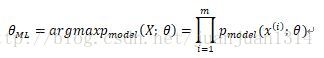
這裡需要說明一下,將資料集中的各資料看做是相互獨立的,因此,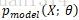
由於多個概率相乘,結果越來越小,很容易被計算裝置四捨五入為0,同時,對數是單調遞增的,因此,用對數累加作最大似然估計效果一樣
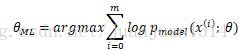
根據分佈函式的期望定義:
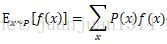
對似然函式除m後,就可以看作是所有x的權重都為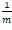
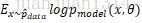
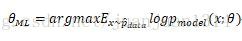
最大似然估計可以看作是把所有引數的出現概率是相等的估計。
實際應用中,估計通常是條件概率,如同分類學習演算法中的
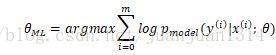
另外,根據
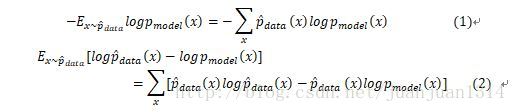
式(1)是模型的負對數似然,由於式(2)的第一項是生成分佈,是固定的,最小化式(1)和最小化式(2)的效果是一樣的。因此,任何一個負對數似然代價函式,與定義在訓練集的經驗分佈和定義在模型的概率分佈之間的交叉熵是等同的。
線性模型中的均方代價函式可以等同於經驗分佈和高斯模型之間的交叉熵。
2. 貝葉斯估計
貝葉斯統計的重點引數未知且不確定,因此作為隨機變數,引數本身也是一個分佈,同時,根據已有的資訊可以得到引數θ的先驗概率,根據先驗概率來推斷θ的後驗概率。
根據貝葉斯規則:
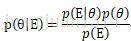
其中,p(θ)是θ的先驗概率,E是觀察到的現象。p(θ│E)表示根據觀察到的現象估計的引數概率分佈,而p(E│θ)是當前引數條件下,現象E出現的概率分佈。
和最大似然估計一樣,預測中觀察到最直接的現象通常是結果(Y),間接一些的是原因(X),因此,
和最大似然估計不同,最大似然估計的模型是固定的,求得使似然函式最大的引數集後,模型就確定下來,就完全可以根據模型和資料預測結果了。但是,貝葉斯估計除了模型需要確定,還需要給定一個先驗分佈的初始模型,通常需要選擇一個常用分佈,並確定一個初始引數集作為先驗分佈。然後得到引數的後驗概率分佈
3.MLE和Bayes估計線性迴歸引數
用這兩種估計的前提是將樣本的模型定為多維高斯分佈,高斯分佈的協方差定為單位矩陣I,要通過確定引數預測均值。
線性迴歸的基本表達:
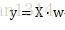
高斯分佈:
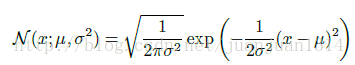
模型定為 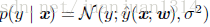
用MLE預測,其對數似然函式:
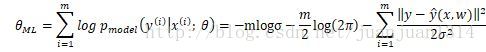
等式前兩項都與w無關,只有最後一項相關,而最後一項等同於均方代價函式。因此,前面提到,線性模型的均方代價函式實際上是經驗分佈和高斯模型的交叉熵。
用Bayes估計:
引數w的先驗分佈初始化為高斯分佈,均值為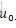
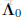
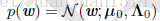
從前面推斷最大似然估計中可以看出,高斯分佈的對數似然函式與均方差代價函式相關,因此,p(w)的似然函式
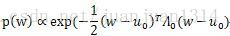
後驗分佈可以表示為:
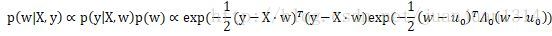
這個等式在《深度學習》5.6節中做如下化簡:
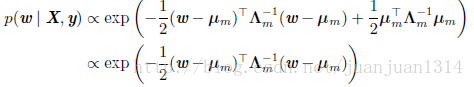
其中, 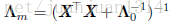
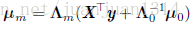
到了這裡,還是不太確定,引數的後驗分佈確定後,在訓練過程中是作為下一次學習的先驗分佈呢,還是用後驗概率通過貝葉斯規則計算下一次學習的p(y|X,w)?如果兩者都不是,那實在不能理解後驗概率的作用了。個人以為第二種的可能性更大。關於這一點,暫時沒有搜尋到滿意的答案,很多關於貝葉斯估計的部落格在講解貝葉斯估計的時候都是用貝葉斯規則來解鎖貝葉斯估計的,說到的點都是先驗概率,個人覺得貝葉斯估計和類似於樸素貝葉斯這種貝葉斯規則的應用還是有差別的。
4. 最大後驗估計(MAP)
MAP是點估計和分佈估計的結合。為什麼需要這要的結合呢?雖然大家說“世界是貝葉斯的”,貝葉斯估計更合理,各引數集合的可能是相同的確實有點武斷,過於簡化了。但從上面用MLE和bayes估計線性迴歸的引數可以看到,純正的bayes估計實際上比較麻煩哦,既要確定模型,還要事先初始化一個先驗概率,估計過程涉及到兩個分佈的運算,最主要的是,引數估計是一個分佈,對於稍微複雜的學習過程,計算就更麻煩了。
實際上,當取估計到的引數分佈概率最大的點作為最佳引數,那麼分佈估計也就變成了點估計。取bayes估計中引數後驗分佈中概率最大的點來估計引數就是最大後驗估計:
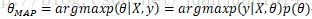
依然對這個似然函式求對數,對數函式是單調的,對最大估計無影響:

等式最右邊第一項是標準的對數似然函式,第二項是先驗分佈的對數。依然帶入先驗分佈,但後驗估計不再是一個全分佈計算了,而是轉化為對數似然計算,計算化簡了很多。對數先驗項本身不需要做最大估計,它如同一個懲罰項。