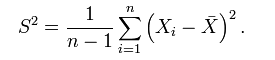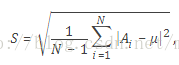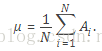樣本方差的與方差
之前做模型擬合的時候需要計算樣本的方差和均值,Matlab的std函式算出來就是不對經,一看才知道matlab的給定的標準差計算公式是:
For a random variable vector A made up of N scalar observations, the standard deviation is defined as
where μ is the mean of A:
The standard deviation is the square root of the variance. Some definitions of standard deviation use a normalization factor of N
w to 1.
也就是分母除以N-1二不是N了,乖乖,這明顯和教科書上定義不一樣嘛,於是百度之,最後在知乎上得到一個比較好的解釋。
作者:魏天聞
連結:https://www.zhihu.com/question/20099757/answer/26586088
來源:知乎
著作權歸作者所有。商業轉載請聯絡作者獲得授權,非商業轉載請註明出處。
上面有答案解釋得很明確,即樣本方差計算公式裡分母為的目的是為了讓方差的估計是無偏的。無偏的估計(unbiased estimator)比有偏估計(biased estimator)更好是符合直覺的,儘管有的統計學家認為讓mean square error即MSE最小才更有意義,這個問題我們不在這裡探討;不符合直覺的是,為什麼分母必須得是
才能使得該估計無偏。我相信這是題主真正困惑的地方。
要回答這個問題,偷懶的辦法是讓困惑的題主去看下面這個等式的數學證明:![]() .
.
但是這個答案顯然不夠直觀(教材裡面統計學家像變魔法似的不知怎麼就得到了上面這個等式)。
下面我將提供一個略微更友善一點的解釋。
==================================================================
===================== 答案的分割線 ===================================
==================================================================
首先,我們假定隨機變數
由此可得![]() .
.
因此![]() 是方差
是方差的一個無偏估計,注意式中的分母不偏不倚正好是
!
這個結果符合直覺,並且在數學上也是顯而易見的。
現在,我們考慮隨機變數的數學期望
是未知的情形。這時,我們會傾向於無腦直接用樣本均值
替換掉上面式子中的
。這樣做有什麼後果呢?後果就是,
如果直接使用![]() 作為估計,那麼你會傾向於低估方差!
作為估計,那麼你會傾向於低估方差!
這是因為: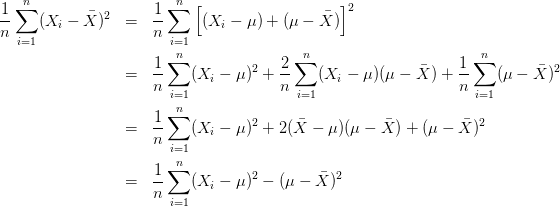
換言之,除非正好,否則我們一定有
![]() ,
,
而不等式右邊的那位才是的對方差的“正確”估計!
這個不等式說明了,為什麼直接使用![]() 會導致對方差的低估。
會導致對方差的低估。
那麼,在不知道隨機變數真實數學期望的前提下,如何“正確”的估計方差呢?答案是把上式中的分母換成
,通過這種方法把原來的偏小的估計“放大”一點點,我們就能獲得對方差的正確估計了:
![]()
至於為什麼分母是而不是
或者別的什麼數,最好還是去看真正的數學證明,因為數學證明的根本目的就是告訴人們“為什麼”;暫時我沒有辦法給出更“初等”的解釋了。
關於公式的證明:
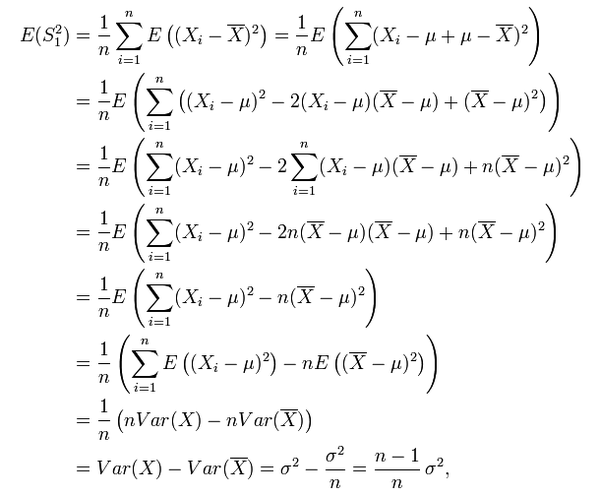
而 (n-1)/n * σ² != σ² ,所以,為了避免使用有 bias 的 estimator,我們通常使用它的修正值 S²: