1.什麼是貝塞爾曲線？

貝塞爾曲線所依據的最原始的數學公式，是早在1912年就廣為人知的伯恩斯坦多項式。簡單來說，伯恩斯坦多項式可以用來證明，在[ a, b ] 區間上所有的連續函式都可以用多項式來逼近，並且收斂性很強，也就是一致收斂。再簡單點，就是一個連續函式，你可以將它寫成若干個伯恩斯坦多項式相加的形式，並且，隨著 n→∞，這個多項式將一致收斂到原函式，這個就是伯恩斯坦斯的逼近性質。
到了1959年，當時就職於雪鐵龍的法國數學家 Paul de Casteljau 開始對伯恩斯坦多項式進行了圖形化的嘗試，並且提供了一種數值穩定的德卡斯特里奧（de Casteljau） 演算法。根據這個演算法，就可以只通過很少的控制點，去生成複雜的平滑曲線，也就是貝塞爾曲線。
而貝塞爾曲線的得名，得歸功於1962年就職於雷諾的法國工程師皮埃爾·貝塞爾（Pierre Bézier），他使用這種方法來輔助汽車的車體工業設計，並且廣泛宣傳，因此大家才都稱他為貝塞爾曲線 。

2.貝塞爾曲線是怎麼畫出來的？

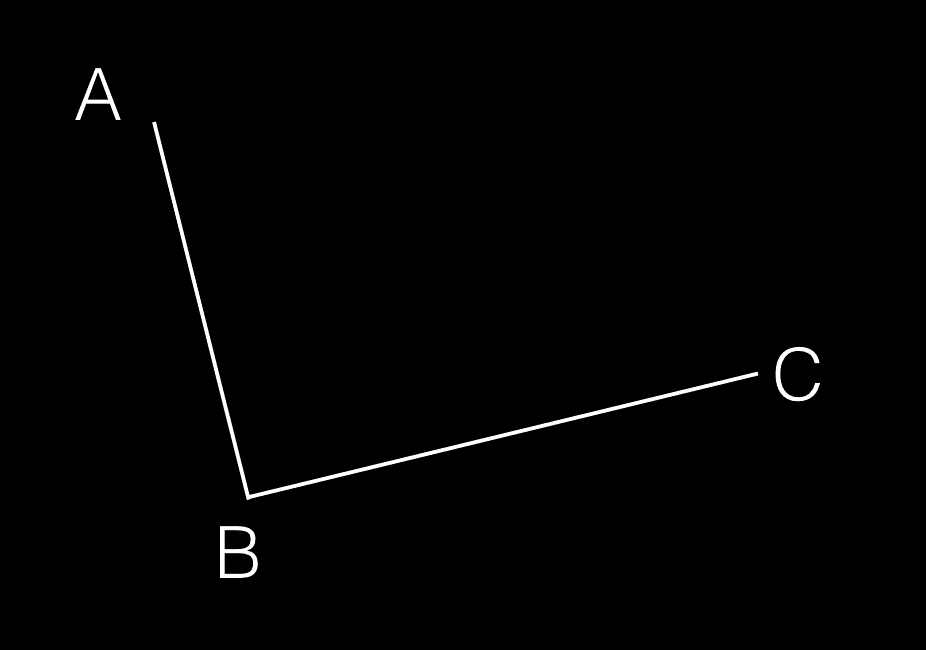
首先，我們在平面內選3個不同線的點並且依次用線段連線。如下所示：

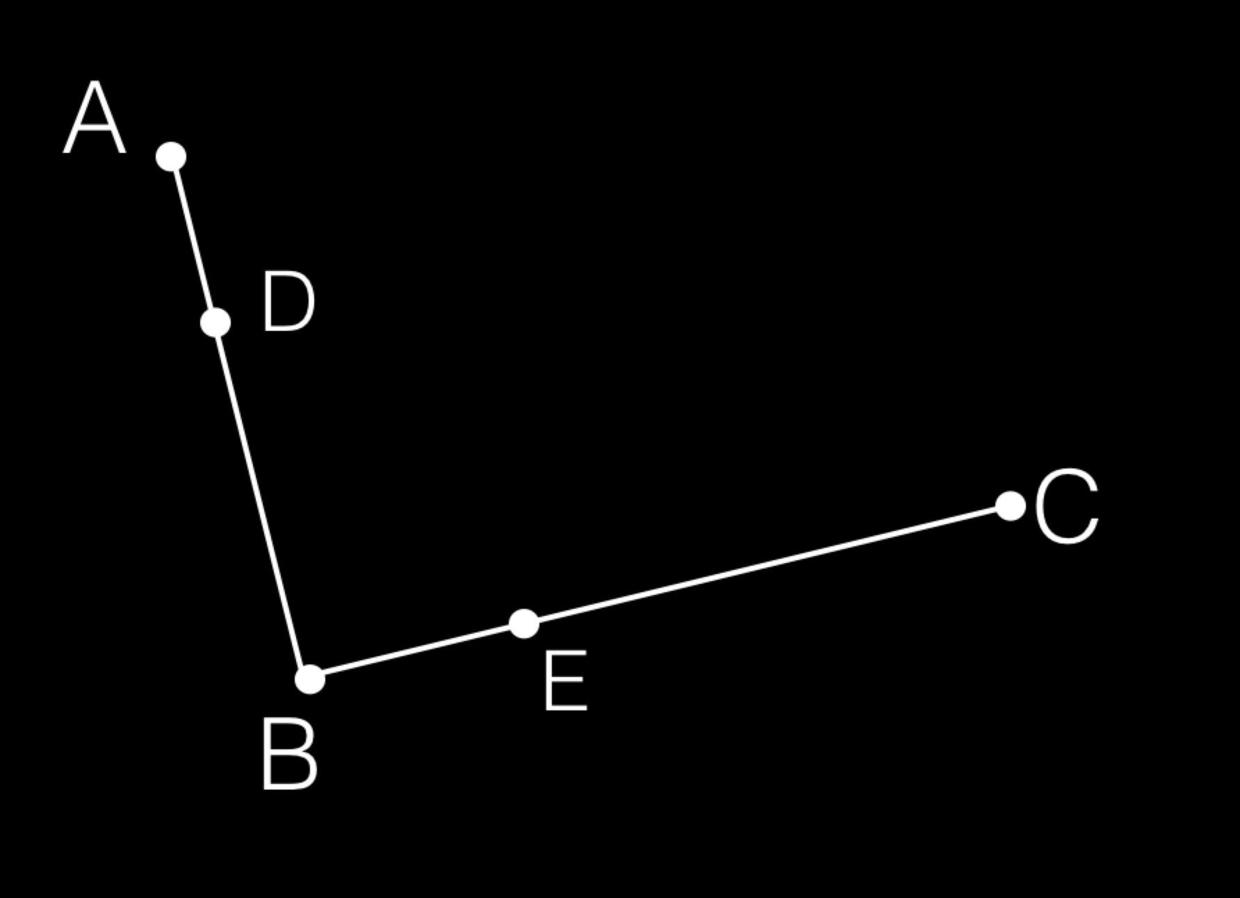
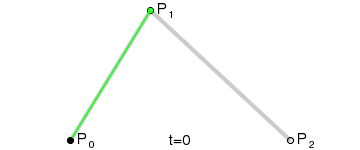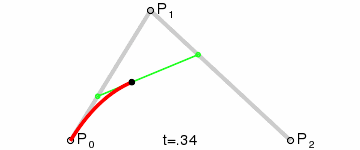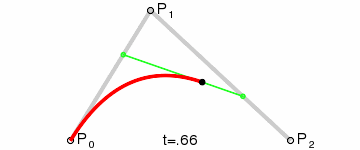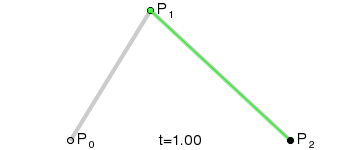
接著，我們在AB和BC線段上找出點D和點E，使得AD/AB = BE/BC：

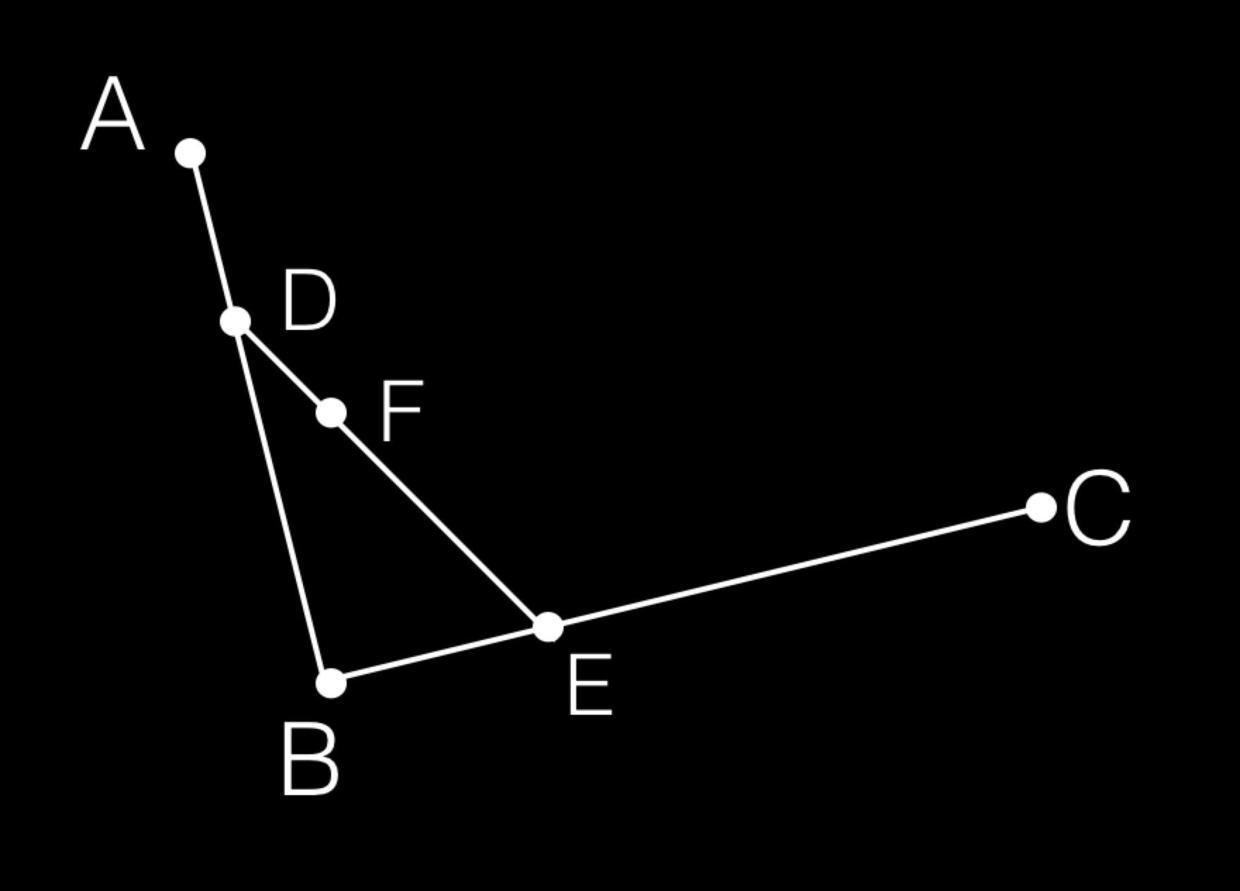
再接著，連線DE，並在DE上找出一點F，使得DF/DE = AD/AB = BE/BC：

然後，根據我們高中所學的極限的知識，讓選取的點D在第一條線段上從起點A，移動到終點B，找出所有點F，並將它們連起來。最後你會發現，你得到了一條非常光滑的曲線，這條就是傳說中的，貝塞爾曲線。
二階貝塞爾曲線動態演示：
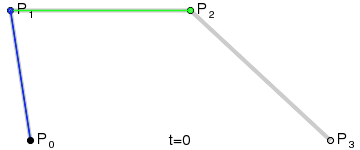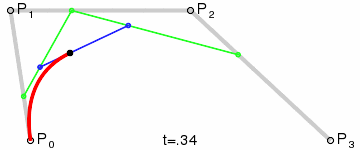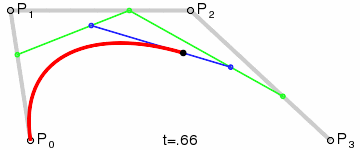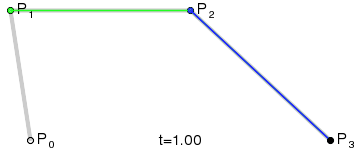
三階貝塞爾曲線動態演示：

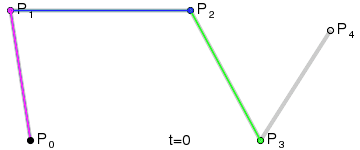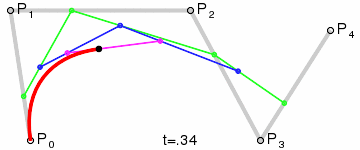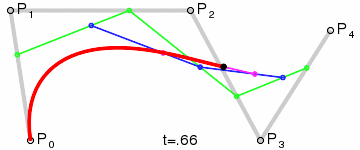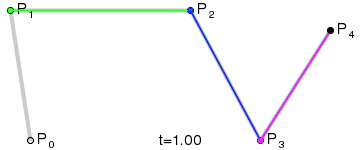
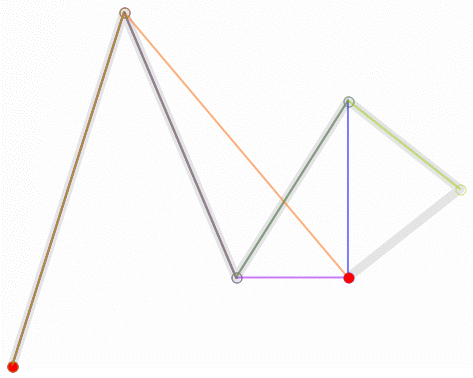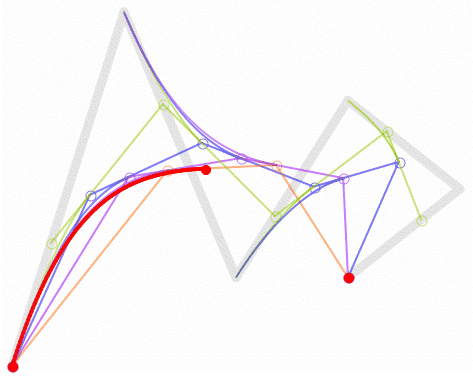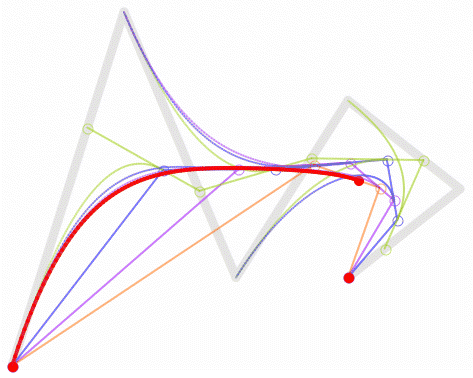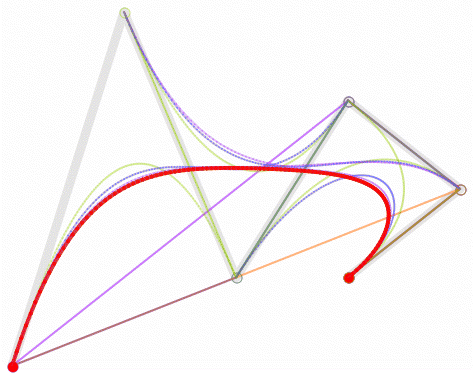
四階貝塞爾曲線動態演示：

五階貝塞爾曲線動態演示：

所以貝塞爾曲線的厲害之處就在這裡，從1-n階的連續函式，他都可以計算得到一條光滑曲線。

3.貝塞爾曲線的特點和用途？

特點一：曲線通過始點和終點，並與特徵多邊形首末兩邊相切於始點和終點，中間點將曲線拉向自己。 特點二：平面離散點控制曲線的形狀，改變一個離散點的座標，曲線的形狀將隨之改變（點對曲線具有整體控制性）。 特點三：曲線落在特徵多邊形的凸包之內，它比特徵多邊形更趨於光滑。 特點四：貝塞爾曲線屬於“平均通過”式曲線。 由於貝塞爾曲線控制簡便，而且它具有很強的描述能力，因此它在工業設計上已經被廣泛使用了。不僅如此，在計算機圖形學領域（特別是向量圖形學），貝塞爾曲線也有著舉足輕重的地位。而作為程式猿，我們經常會用貝塞爾曲線來繪圖（由貝塞爾曲線畫出來的圖很光滑~），來做動畫（很自然的動畫）等等。也就是由於它可以發揮的作用領域太廣了，因此我們時不時都會聽到這個名字。

4.如何用貝塞爾曲線？

首先，要明確的一點是，對於貝塞爾曲線來說，最重要的點是，資料點和控制點。
資料點： 指一條路徑的起始點和終止點。
控制點：控制點決定了一條路徑的彎曲軌跡。 根據控制點的個數，貝塞爾曲線被分為一階貝塞爾曲線（0個控制點）、二階貝塞爾曲線（1個控制點）、三階貝塞爾曲線（2個控制點）等等。
而系統給我們提供了一個叫做UIBezierPath類，用它可以畫簡單的圓形，橢圓，矩形，圓角矩形，也可以通過新增點去生成任意的圖形，還可以簡單的建立一條二階貝塞爾曲線和三階貝塞爾曲線。

5.參考資料

http://www.cnblogs.com/zhangrunchao/p/6178366.html
JOHNH.MATHEWS), KURTISD.FINK. 數值方法(MATLAB版)[M]. 電子工業出版社, 2005.