本文轉自中國人工智慧學會通訊第3期，已獲授權，特此感謝！
歡迎人工智慧領域技術投稿、約稿、給文章糾錯，請傳送郵件至[email protected]
3月3日，中國人工智慧學會AIDL第二期【人工智慧前沿講習班】在北京中科院自動化所舉行，來自清華大學電腦科學與技術系的朱軍副教授分享了題為《貝葉斯學習前沿進展》的演講。內容主要分為三部分：貝葉斯基本理論、模型和演算法；可擴充套件的貝葉斯方法；深度生成模型。本文為第一部分：貝葉斯基本理論、模型和演算法。

非常感謝周老師給這個機會讓我跟大家分享一下。我今天想和大家分享的是，在深度學習或者大資料環境下我們怎麼去看待相對來說比較傳統的一類方法——貝葉斯方法。它是在機器學習和人工智慧裡比較經典的方法。

類似的報告我之前在CCF ADL 講過，包括去年暑假周老師做學術主任在廣州有過一次報告，大家如果想看相關的工作，我們寫了一篇文章，正好我今天講的大部分思想在這個文章裡面有一個更系統的講述，大家可以下去找這篇文章讀。

這次分享主要包括三個部分：

第一部分：基本理論、模型和演算法

貝葉斯方法基礎
正則化貝葉斯推理和案例

第二部分：可擴充套件的貝葉斯方法

線上學習
分散式MCMC

第三部分：深度生成模型

第一部分：貝葉斯基礎和正則化貝葉斯

貝葉斯方法概念是比較簡單的，一般情況下我們做貝葉斯推理，用了一個核心的工具叫貝葉斯定理或者貝葉斯準則，實際上寫出來就是這麼一個簡單的公式，大家學概率基本上都學過這個。公式裡有幾個基本的物件，我們用θ 描述模型的引數，這個模型可以是神經網路、線性模型，或者SVM，引數都用θ 來描述；D 是我們的訓練集；π(θ) 是先驗分佈，是我們看到資料之前對模型本身分佈的描述；p(D|θ) 是似然函式，給定一個模型θ 的情況下描述這個資料的似然。我們的目標是想獲得這個後驗分佈，是看到資料之後再重新看模型本身的分佈情況。這是1763 年當時貝葉斯生前沒有發表的文章裡面，最早闡述了這個公式，最後正式發表了。

在機器學習裡面，貝葉斯法則可以做什麼？

首先，預測問題。我們用大M來描述model class，比如線性模型、非線性模型，model class裡面有多個具體的模型，我們還是用引數θ表示。對新來的樣本做一個預測，比如算它的似然，這樣可以用前邊推出來的後驗分佈來做一個積分。這個是給定模型下樣本的似然，這是所有可能模型的分佈。本質上是做了一個平均，這個思想實際上跟周老師的整合學習的思想是比較相近的，我們也是對很多種模型做了一個加權的平均，只是說在這個地方模型可能有無限多個，我們是用概率分佈來去描述它。

這個似然函式通常假設在給定模型引數的情況下，測試資料與訓練資料是獨立的，這就是我們通常說的獨立同分布的假設。

除了做預測，我們還可以做不同模型的比較、模型的選擇。比如說我們要做分類問題，到底是要選線性的模型還是深度學習的非線性模型，這是在做模型選擇的問題。這個問題可以描述成這樣：我們用M1表示一個model class，可能是一個線性模型，我們用M2表示另外一個model class，是非線性模型，我們在同樣資料集D的情況下，我們可以去比較這兩個量哪個大，這個量是描述的在M1下我們觀察到訓練集的一個似然，另外一個是在M2的情況下觀察的資料集似然，可以通過這個比較看我應該選擇哪一種模型，這是一個用貝葉斯方法做模型選擇的一個基本的規則。

為什麼要用貝葉斯方法？

做貝葉斯的人會告訴你很多的理由，我們後邊從例子裡邊也會看到一些答案。這裡給大家簡單講一個，概率論的結果告訴我們實際上在很多情況下對資料的建模是存在這種貝葉斯的模型來刻畫的。這有一個基本性質叫Infinite Exchangeability，假如你資料有N個樣本，如果將它們任意交換順序，這些資料的聯合分佈不變化，也即是我們通常說的和序列無關，那麼它的聯合分佈可以寫成貝葉斯的形式—存在一個模型和對應的分佈，你通過積分的形式可以刻畫整個分佈。如果用圖示畫一下，在給定這個模型的情況下，資料是完全獨立的，我們叫條件獨立性，這是概率圖模型裡的一個非常重要的概念。

稍微提一點，可交換性比前面講的獨立同分布更廣泛一點，可交換的資料可以不是獨立同分布的。另外，這個定理只告訴你存在，但是後面的問題是我們不知道具體的模型應該是什麼樣的，比如說是線性模型、非線性模型，用什麼樣的模型去刻畫，這是統計建模要解決的問題。

先驗（Prior）從哪裡來？

在貝葉斯里有兩個流派，一個是客觀貝葉斯，另一個是主觀貝葉斯。所謂客觀貝葉斯，就是希望能夠把先驗的影響儘量弱化，所以會研究一些noninformative priors，就是你用貝葉斯的結果像用統計的方法得到結果一樣，有一些統計性質。而主觀貝葉斯，實際上是更希望利用貝葉斯框架的靈活性，因為貝葉斯框架給了你一個先驗的分佈，你可以在先驗上做文章，我們後邊也會有些例子來講怎麼去利用先驗提供的靈活性，來做具體的學習任務或者解決問題。用主觀貝葉斯的好處之一是，當你的資料足夠多的時候，可以通過先驗引入一些知識來幫助你學習，這個尤其在交叉學科裡，比如用貝葉斯方法做認知或者神經科學，是大家比較喜歡用的方法。

當然還有另外一些具體的技術，我可以相信這個prior，但是我儘量弱化prior裡邊引數的影響，這裡面有一種技術叫“層次的prior”。有一個基本的假設，這個π裡面的引數叫超引數，它離我這個產生資料的模型越遠的話影響就越弱，實際上利用這種基本假設，就可以構建多層的prior。

從這裡面可以看到，貝葉斯本身就是一個多層的，和深度學習的多層表示本質是一樣的，只不過這裡邊完全用概率的方式來刻畫。當然還有一些近似的方法，做一些empirical prior，通過資料估計出來。好處是計算相對比較簡單，不好的地方是多次用訓練資料，會得到一些過擬合的問題。

我們如何計算積分？

我們前面已經看到，不管是在最基本的貝葉斯運算或者是在多層先驗裡面都會反覆用到積分運算，這是在用貝葉斯方法時面臨的最討厭的事情，因為這裡的積分不像我們學微積分時的那種一元或者二元簡單的積分運算，這裡的積分可能是非常高維的積分。假設我們用一個線性模型，當特徵100維時，我這個就是100維的積分，如果更高維的，比如說上千、上萬維，這個積分相應更高維。這裡面有很重要的計算問題，我怎麼用數值的方法來算這個積分。這是在這種不確定性或者概率推理裡邊要解決的主要目標。

近似貝葉斯推理

我用一頁PPT簡單給大家介紹了一下。因為積分非常難算，所以通常情況下會用一些近似，尤其是在機器學習裡面，大家用的貝葉斯方法通常是一個近似的貝葉斯推理。

這裡面我列舉了幾個比較常用的經典近似貝葉斯推理的方法。

首先第一種，變分的方法。變分的基本原理是把一個要解的問題，通過引入一個變數變成一個優化的問題。這樣做的好處是，你可以在優化問題中引入一些約束，讓問題簡化，以達到快速求解的過程；但是也會帶來壞處，如果你的約束比較嚴格的話，近似的程度就會變差。

下面一種是非常通用而且理論上精確的方法，它是基於隨機模擬的，我們叫MCMC的方法，它是通過構造一個隨機過程來逐漸逼近你要的分佈，通過這個隨機過程不斷的取樣，達到刻畫目標分佈的結果。現在面臨的挑戰是：1）當資料比較多的時候，怎麼去做這個計算；2）在高維空間裡面怎麼去做隨機的模擬；3）當我們的模型變得複雜的時候，比如最後會給大家講的深度產生式模型裡邊有多層的隱含變數，像深度學習一樣，這種模型下我怎麼還去做MCMC。這些挑戰同樣存在於變分近似方法裡面，現在仍然是研究的熱點。還有一些相關的，比如像EP或者拉普拉斯近似，基本上可以理解為變分的一種特殊類別。

貝葉斯方法面臨的挑戰

其實我前面已經給大家簡單講了一些，這個是我們的一個總結，如果想去做貝葉斯機器學習的話，基本面臨著幾個方面的問題。

第一點，是基本理論上的問題。我前面講的貝葉斯方法概念非常簡單，它的核心是貝葉斯定理。貝葉斯定理已經250多年了，它存在一些自己的侷限，我們怎麼從基本資訊處理準則的角度來重新理解它，去做更靈活的推理。

第二點，是關於計算方面的。有了模型、有了推理框架之後我怎麼去做高效的計算、怎麼做高精度的計算。

第三點，對不同場景怎麼去做建模。將貝葉斯方法應用到不同場景時，你要去理解你的問題，找到合適的模型。

我後面基本上圍繞這三個方面給大家講。第一個方面，給大家提出一種比較新的觀點來看經典的貝葉斯定理，告訴大家怎麼去擴充套件它的靈活性。第二個是關於Scalability，我怎麼算比較快。最後一個，貝葉斯方法和深度學習怎麼結合，既利用深度學習的好處又保持貝葉斯在概率建模和推理的能力。

KL散度

我們先從最基本的概念開始，可能大家學過模式識別或者訊號處理，都會接觸過這個概念，叫KL散度，它描述兩個概率分佈之間的差異有多大。

首先，我們可以通過優化的方式重新審視貝葉斯推理。對任意一個分佈我可以來做這件事情，這個是我們的目標P，我們可以找一個Q分佈，它是一個well defined的分佈，我可以通過最小化它們之間的KL，取最小值的時候兩個是相等的，這是非常簡單的道理。

我們可以把這個基本過程用到貝葉斯定理裡。貝葉斯推理的目標是找到這個後驗分佈，將它代入這個目標函式裡，現在Q是我假設的分佈。這樣，我們得到了一個優化的問題。這是我們原來的貝葉斯定理，如果這個目標函式等於0的話，實際上Q等於我們想要的P（C/D）的後驗分佈。目標函式的第一項是限制我們的後驗分佈不能離先驗分佈太遠，後面一項實際上是描述了對資料集的擬合程度。

這樣的話，我們獲得了一種新的角度來看貝葉斯推理在幹嗎。有了這種新的理解之後，我們可以做的事情有很多。

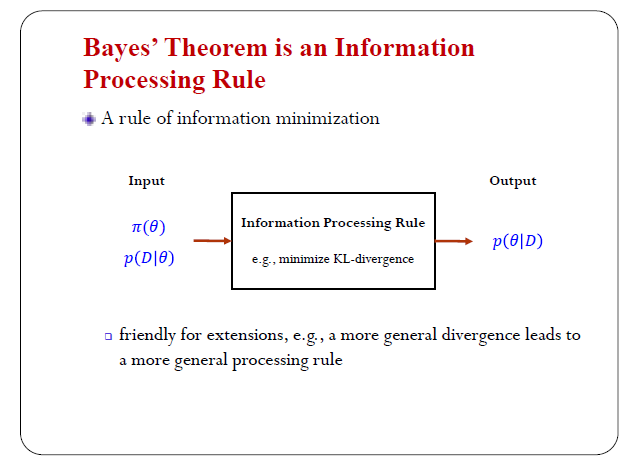
貝葉斯定理作為一種資訊處理準則

實際上，我們說貝葉斯定理或者貝葉斯推理是資訊處理的一種準則。在資訊理論裡，我們有一個通道，有輸入和輸出。在做貝葉斯推理時，我們的輸入是一個先驗分佈和一個似然函式，輸出是一個後驗分佈。有了這種觀點之後，我們可以做很多擴充套件。大家可以想，我的輸入、輸出可以保持不變，但我可以替換資訊處理的準則。我可以把這裡邊資訊處理的準則拿掉，做的比經典貝葉斯更加普適。

這種基於優化的解釋，實際上在上世紀80年代就有統計學家提出過，E.T. Jaynes是比較有名的統計學家，對我們前面講的優化解釋做了一些comments，它給經典的貝葉斯提供了一個新穎（fresh）的解釋，可以讓貝葉斯方法更廣泛被應用，而且可以激發（stimulate）新的發展。我們在2010年左右重新審視了這個思路，並依此為基礎又發展了一些更普適的貝葉斯推理準則，後面我會介紹。

上述優化的觀點可以啟發我們把貝葉斯方法和基於風險最小化（risk-minimization）的機器學習框架有機結合。機器學習深入研究過risk-minimization以及相關的優化工具，在我們的框架下可以融合貝葉斯推理，得到一個更靈活的資訊處理準則。

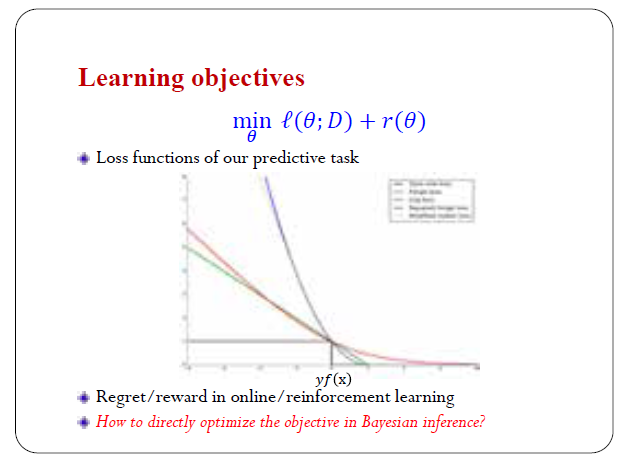
學習目標

在機器學習和模式識別裡，大家比較熟悉的是這個損失函式優化問題。比如說，我要做分類，我要訓練神經網路，第一項是一個損失函式，它度量了在訓練集的錯誤率；第二項是我們想加的正則化項，目的是保護這個模型避免過擬合、避免發散，這是一個基本框架。這些東西在機器學習裡基本上和貝葉斯是不搭邊的，不會和貝葉斯放在一起來討論。

還有一些，比如現在又引起大家很多關注的增強學習/線上學習，它的目標是優化Regret/reward，也有一個目標函式來度量。那麼，一個問題是這些傳統的方法能不能與貝葉斯有機融合？

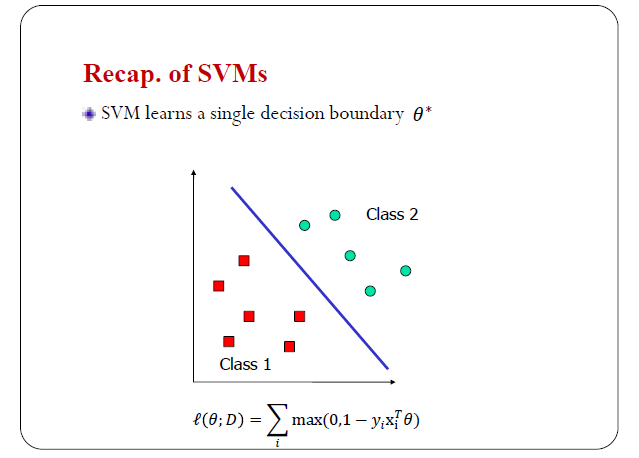
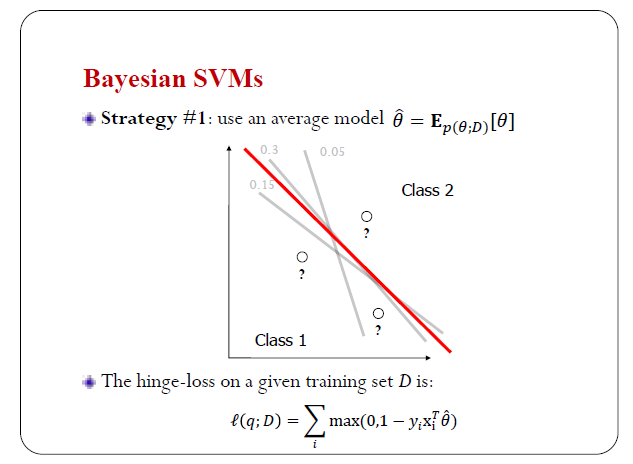
先給大家看一個簡單的例子，是線性的SVM，它的目的是想找一個線性平面把不同類別區分開。

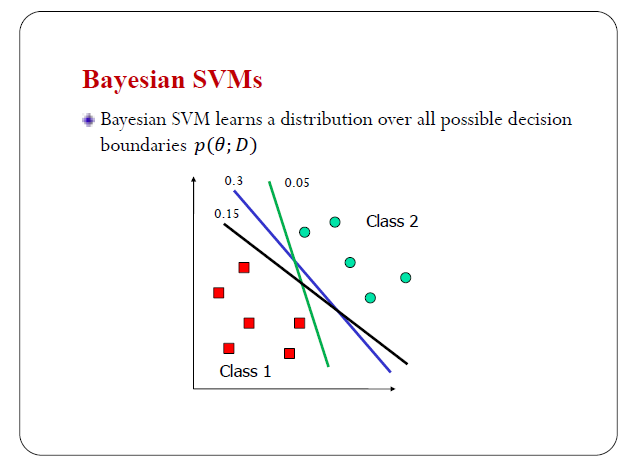
我們說有一個叫貝葉斯的SVM。

我們可以先簡單的把貝葉斯的思路套到SVM上來看發生了什麼事。傳統的SVM是找一個決策面，按照一定的最優準則來找。貝葉斯的思想是：我們可以有無窮多個決策面，但是每個決策面有一定的概率。考慮這個簡單例子，設有有限多個可能決策面，如果隨機取樣的話，比如你取樣100次，這個藍色的線可能會出現30次，這個綠色的線可能出現5次，這個線可能出現15次。這裡邊畫的幾條線，都可以把這幾個樣本分開。

假設這個分佈是已經知道的，我們怎麼做分類判別。根據不同的判別準則，得到損失函式是不一樣的。比如：我現在來了這些打問號的測試樣本，我想問，那這些測試樣本到底屬於哪個類別？

因為這裡面決策面是不確定的，我們可以有兩種策略來做判別。

一種是模型平均：先對這種模型做平均，在做判別。比如，我們可以取這個分佈的均值，對應於這個紅色的面（下圖中顏色較深的線），我可以用這個紅色平面來做判別，這是一種思路。它對應的損失函式就可以像經典的SVM一樣計算，因為取得平均之後就是一個決策面了，和我們傳統的問題一樣。

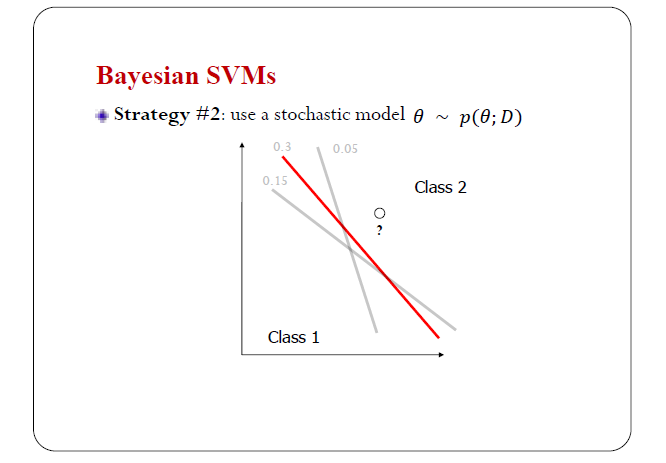
還有一種模型叫隨機模型，它實際上是這麼做的：新來了一個測試樣本，我從後驗分佈裡面隨機取樣一個模型，比如對這個測試樣本我隨機取樣是這個紅色的線（下圖中顏色較深的線），然後用它來做判別。另外一個樣本來了之後，我再隨機取樣一次，可能採集的是這個。

下邊再來一個樣本，我再取樣一次，可能得到和第一次取樣一樣的決策面，然後用它來判別。

因為分類平面是隨機的，所以我還要去度量它的一個損失函式。所以，我們可以先假設這個分類面是固定的，做一個判別；然後對損失函式求期望。

放在一起來看一下。我們第一種策略是平均模型，第二個是隨機模型，這兩個在理論上有一些關係，這裡我不細說了。我們有了這個loss函式之後，就可以直接進行優化，這是從貝葉斯的角度做SVM的方法。。

有了上述問題之後，怎麼去求解？對於第一種平均模型，可以通過用凸優化的思路來求解。當模型是線性的，如果先驗是高斯，你的後驗分佈還是一個高斯。這實際上退化到傳統的SVM。你還可以拓展，利用核方法來拓展非線性的模型，這都是可以的。

對於第二種，給定先驗，可以求出一般解。這裡有一個問題，這個後驗分佈通常沒有一個解析形式，所以大家研究怎麼去做推理。這有一個比較好的方法，大家感興趣可以去看，用了統計裡經常用的資料增廣（data augmentation）。

它（資料增廣）的基本過程：原來這個分佈不太好做，引入一個額外變數過來。它的條件是說，保證邊緣分佈還是原來的分佈。在這個聯合分佈下你可以做吉布斯取樣，每一步都很簡單，比如：第一步可能是高斯，第二步也是某種標準分佈。這樣可以不斷迭代進行取樣。具體細節，大家可以看Polson&Scott有一篇文章。

貝葉斯SVMs隱含變數

這種貝葉斯的觀點可以帶來一些額外的好處。跟深度學習中表示學習的思想一致，在貝葉斯SVM裡，我們可以考慮隱含變數，也可以加很多層的隱含變數，來學這些隱變數的分佈。在神經網路裡可能學具體的取值，在概率模型裡學分佈，這是它們的一個差別。這裡有一個典型的例子，叫主題模型，在文字分析裡面用的比較多。

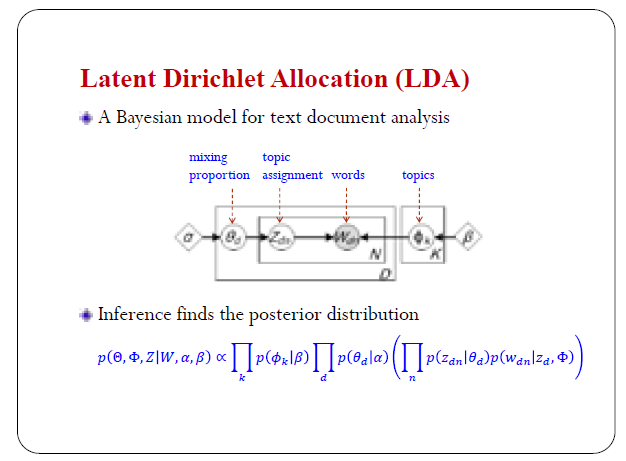
這是一個主題模型描述文字生成的一個過程。

它的基本假設是文件是有若干主題刻畫的。假設這裡有2個主題，大家從keyword裡能看出來相應的語義，比如：第一個是關於影象，另一個是關於電力相關的東西。在第一個文件裡，我用顏色區分相應的主題，比如說這裡面的單詞以0.8的概率從第一個主題生成，相應的， 0.2的概率從另一個主題生成。對於第二個文件，混合分佈是（0.3、0.7）。整個過程可以描述成一個非常經典的層次貝葉斯方法。

這是它的圖模型，W是觀察到的文本里面的單詞，每個單詞對應一個topic assignment。下面有一個混合概率，上面有一個先驗，這邊是我們要學的topic。它定義了這個聯合分佈。

LDA非常經典，2003年的一篇論文可能引了近2萬次，表明它在很多地方用。它有一個好處是可以代到很多複雜的模型裡面。後期的工作基本上可以總結成有大概三個方面。一個是先驗，比如我要考慮主題之間的相關性，可以用非共軛的logistic-normal先驗分佈。還可以做時間序列資料的分析，或者關係網路資料的分析等。

這裡給大家簡單看一個例子，如何將貝葉斯SVM用於主題模型。我們可以用同樣的原理，在主題模型上定義貝葉斯SVM分類器，通過最優化目標函式，實現兩種功能：1）學習隱含主題；2）學習分類器。在定義分類器時，我們採用如前所述的兩種策略——平均模型和隨機模型，分別會得到相應的模型。這是一些真實資料上的測試結果，能夠體現這種方法的有效性。

下面有一些特定的分析，可能有人會問，做後驗約束和在先驗上加約束會有什麼差別？我現在告訴大家，在先驗上做的約束都可以在後驗上做，是我們的一個特例。另外，我們在後驗上做約束可以更靈活，也就是，有些後驗分佈在經典的方法得不到。

這是一個直觀的解釋。大家做貝葉斯方法，可以有各種的引數化、無引數化的貝葉斯模型，都是在這個平面裡做的。我們做的事情實際上是增加了一個維度，它和之前的兩個維度是獨立的，因此，可以在這上面做很多事情。首先，可以把經典的模型做到最大間隔學習，得到新的模型。其次，我們也可以把知識資訊引入貝葉斯推理中。因此，我們可以形成一個有機的框架，包括知識、學習/推理、以及最下邊的統計建模。

這是第一部分，我想和大家分享的是：我們做貝葉斯方法，現在已經不侷限在經典的貝葉斯框架，實際上有一些新的發展。
（本文是根據中國人工智慧學會人工智慧前沿(AIDL) 講習班朱軍副教授現場分享整理的文字報告，雷鋒網［AI 科技評論］編輯整理）

【CSDN_AI】熱衷分享 掃碼關注獲得更多業內領先案例