濾波反投影重建演算法實現及應用（matlab）

1. 濾波反投影重建演算法原理

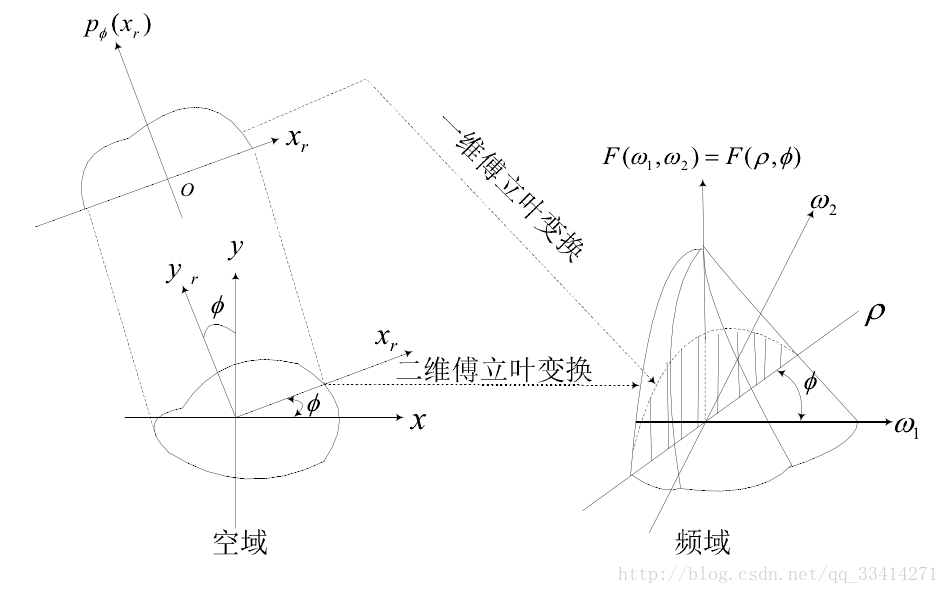
濾波反投影重建演算法常用在CT成像重建中，背後的數學原理是傅立葉變換：對投影的一維傅立葉變換等效於對原影象進行二維的傅立葉變換。（傅立葉中心切片定理）

CT重建演算法大致分為解析重建演算法和迭代重建演算法，隨著CT技術的發展，重建演算法也變得多種多樣，各有各的有特點。本文使用目前應用最廣泛的重建演算法——濾波反投影演算法（FBP）作為模型的基礎演算法。FBP演算法是在傅立葉變換理論基礎之上的一種空域處理技術。它的特點是在反投影前將每一個採集投影角度下的投影進行卷積處理，從而改善點擴散函式引起的形狀偽影，重建的影象質量較好。

上圖應可以清晰的描述傅立葉中心切片定理的過程：對投影的一維傅立葉變換等效於對原影象進行二維的傅立葉變換

傅立葉切片定理的意義在於，通過投影上執行傅立葉變換，可以從每個投影中得到二維傅立葉變換。從而投影影象重建的問題，可以按以下方法進行求解：採集不同時間下足夠多的投影（一般為180次採集），求解各個投影的一維傅立葉變換，將上述切片彙集成影象的二維傅立葉變換，再利用傅立葉反變換求得重建影象。

投影相關知識請參考fbp的matlab實現

2. 濾波反投影重建演算法過程（以平行束為例）

投影重建的過程是，先把投影由線陣探測器上獲得的投影資料進行一次一維傅立葉變換，再與濾波器函式進行卷積運算，得到各個方向卷積濾波後的投影資料；然後把它們沿各個方向進行反投影，即按其原路徑平均分配到每一矩陣單元上，進行重疊後得到每一矩陣單元的CT值；再經過適當處理後得到被掃描物體的斷層影象
演算法步驟如下：
1. 將原始投影進行一次一維傅立葉變換
2. 設計合適的濾波器，在φ_i的角度下將得到原始投影p(x_r,φ_i)進行卷積濾波，得到濾波後的投影。
3. 將濾波後的投影進行反投影，得到滿足x_r=r cos⁡（(θ - φ_i)）方向上的原影象的密度。
4. 將所有反投影進行疊加，得到重建後的投影。

3. 濾波器(濾波函式)和內插函式的選取

由於直接使用反投影演算法會存在兩個對實驗結果影響很不好的因素：

1. 不準確的資料重建影象就會產生各種偽影。
2. 投影的資料是天然離散的，處理不當的話會產生很大的誤差。

常見的濾波器有R-S濾波函式和S-L濾波函式。R-L濾波函式濾波計算簡單，避免了大量的正弦、餘弦計算，得到的取樣序列分是分段現行的，並沒有明顯的降低影象質量，所以重建影象輪廓清楚，空間解析度高。

常見的插值方法有最近鄰插值和雙線插值，最近鄰插值即將離散點中間的缺失值用離它最近的整數處的投影值來替代。

4. FBP的matlab實現

使用R-L濾波器和最近鄰插值方法

clc,clear;
%% 各個引數資訊
%重建後圖片畫素個數
M=512;%建議先和接收感測器的個數一樣

%旋轉的角度 180次旋轉
theta=xlsread('angles_180_3.xlsx','Sheet1','a2:a181');

%投影為512行，180列的資料，列的資料對應每一次旋轉，512個接收感測器
R=xlsread('Accessory_A.xls','附件3');

%由投影進行反變換
size(R,1);%512

% 設定快速傅立葉變換的寬度
width = 2^nextpow2(size(R,1));  

%% 對投影做快速傅立葉變換並濾波
%傅立葉變換
proj_fft = fft(R, width);

% filter 濾波
% R-L是一種基礎的濾波演算法
filter = 2*[0:(width/2-1), width/2:-1:1]'/width;

% 濾波後結果 proj_filtered
proj_filtered = zeros(width,180);
for i = 1:180
    proj_filtered(:,i) = proj_fft(:,i).*filter;
end
figure
subplot(1,2,1),imshow(proj_fft),title('傅立葉變換')
subplot(1,2,2),imshow(proj_filtered),title('傅立葉變換+濾波')

%% 逆快速傅立葉變換並反投影
% 逆快速傅立葉變換 proj_ifft
proj_ifft = real(ifft(proj_filtered)); 
figure,imshow(proj_ifft),title('逆傅立葉變換')

%反投影到x軸，y軸
fbp = zeros(M); % 假設初值為0
for i = 1:180
    rad = theta(i);%弧度， %這個rad 是投影角，不是投影線與x軸夾角，他們之間相差 pi/2
    for x = 1:M
        for y = 1:M
            %{
            %最近鄰插值法
            t = round((x-M/2)*cos(rad)-(y-M/2)*sin(rad));%將每個元素舍X入到最接近的整數。
            if t<size(R,1)/2 && t>-size(R,1)/2
                fbp(x,y)=fbp(x,y)+proj_ifft(round(t+size(R,1)/2),i);
            end
            %}
            t_temp = (x-M/2) * cos(rad) - (y-M/2) * sin(rad)+M/2  ;
             %最近鄰插值法
            t = round(t_temp) ;
            if t>0 && t<=512
                fbp(x,y)=fbp(x,y)+proj_ifft(t,i);
            end
        end
    end
end
fbp = (fbp*pi)/180;%512x512 原影象每個畫素位置的密度

xlswrite('problem2_origin.xlsx',fbp,'Sheet1');%將得到的重建後的影象資料寫入
% 顯示結果
figure,imshow(fbp),title('反投影變換後的影象')

其中每一個檔案都有作用的說明，如需原始檔請留言哈。（如有錯誤請指正）
fbp演算法實現案例

github程式碼下載 別忘了給star喲~

都看到這裡了，不如幫我投個票唄~
本人正在才加2018 CSDN部落格之星的評選，NO.77 “土豆洋芋山藥蛋”，請投我一票，謝謝大家寶貴的一票~

參考文獻：

【1】 範慧贇.CT 影象濾波反投影重建演算法的研究[D].碩士學位論文,西北工業大學,2007.
【2】 餘曉鍔,龔劍,馬建華等.CT 原理與技術[M].北京:科學出版社,2013,95-97.
【3】 毛小淵. 二維CT影象重建演算法研究[D].南昌航空大學,2016.
【4】 洪虹. CT中金屬偽影的校正研究[D].南方醫科大學,2013.
【5】 範慧贇. CT影象濾波反投影重建演算法的研究[D].西北工業大學,2007.