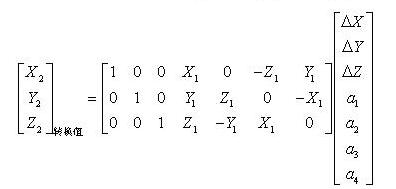利用七引數進行CGCS2000座標系到西安80座標系的轉換
問題
因為工作,需要把CGCS2000座標系下的座標轉到西安80座標系下,中間由於用到了七引數,所以要進經過到空間直角座標系的轉換,然後再轉換到西安80大地座標下,最後再投影到西安80座標的某度帶。
要求是輸入CGCS2000下的大地座標,最後輸出西安80下的平面座標。那麼這項工作可以分為以下幾個步驟:
1.CGCS2000下的大地座標到CGCS2000下的空間直角座標的轉換;
2.CGCS2000下的空間直角座標經過七引數轉換,得到西安80下的空間直角座標;
3.西安80下的空間直角座標向西安80下的大地座標轉換;
4.西安80下的大地座標進行高斯投影,得到平面座標。
大地座標到空間直角座標的轉換
根據轉換公式:
private double[] dd2kjzj(double[] dd){
double a=6378137,b=6356752.314;
double ee=(a*a-b*b)/(a*a);
double L=Math.toRadians(dd[0]),B=Math.toRadians(dd[1]),H=dd[2];
double N=a/Math.sqrt(1-ee*Math.sin(B)*Math.sin(B));
double X=(N+H)*Math.cos(B)*Math.cos 注:函式裡面的a,b的值是CGCS2000(和WGS84相同)下的。其他座標系下的大地座標向空間直角座標的轉換公式都是相同的,只是ab的值需要改動。
利用七引數進行座標轉換
得到空間直角座標後就可以利用七引數進行座標轉換了。具體的七引數求解這裡不進行討論,有意向的網友可以自行百度。轉換公式如下圖所示:
/*七引數運算*/
private double[] qicanshu(double[] source){
double tX,tY,tZ;
tX=dx+source[0]*(1+k)+Oz*source[1]-Oy*source[2];
tY=dy+source[1]*(1+k)-Oz*source[0]+Ox*source[2];
tZ=dz+source[2]*(1+k)+Oy*source[0]-Ox*source[1];
return new double[]{tX,tY,tZ};
} 方法中的source陣列是CGCS2000座標系下的空間直角座標
dx,dy,dz是偏移量
Ox,Oy,Oz是旋轉量
k是縮放因子
空間直角座標到大地座標的轉換
這個轉換就是前面所示的逆運算,如下圖
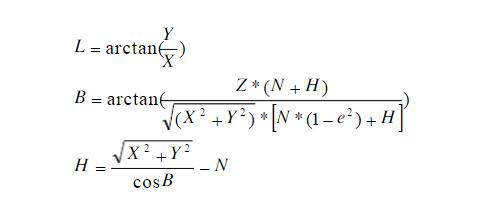
轉換比較複雜,需要進行迭代運算。
private double[] kjzj2dd(double[] kjzj){
double X=kjzj[0],Y=kjzj[1],Z=kjzj[2];
double a=6378140;
double f=1/298.257;
double e2=2*f-f*f; //e^2;
double L=Math.toDegrees(Math.atan(Y/X)+Math.PI);
double B2=Math.atan(Z/Math.sqrt(X*X+Y*Y));
double B1;
double N;
while (true){
N=a/Math.sqrt(1-f*(2-f)*Math.sin(B2)*Math.sin(B2));
B1=Math.atan((Z+N*f*(2-f)*Math.sin(B2))/Math.sqrt(X*X+Y*Y));
if(Math.abs(B1-B2)<0.0000000001)
break;
B2=B1;
}
double H=Z/Math.sin(B2)-N*(1-e2);
double B=Math.toDegrees(B2);
return new double[]{L,B,H};
}高斯投影(正算)
在得到西安80座標下的大地座標後,需要進行高斯投影,這樣才能夠得到平面座標。由於這個計算公式更加的複雜,公式什麼的就不再列了。
//只適用於西安80下的座標投影,程式碼來源於網際網路,經測試還不錯
private double[] dd2pm(double[] dd){
double L=Math.toRadians(dd[0]),B=Math.toRadians(dd[1]);
//輔助量
double cosB = Math.cos(B);
double sinB = Math.sin(B);
double cosB_2 = cosB * cosB;
double l = L - Math.toRadians(Lo);
double ll = l * l;
//計算係數
double N = 6399596.652 - (21565.045 - (108.996 - 0.603 * cosB_2) * cosB_2) * cosB_2;
double a0 = 32144.5189 - (135.3646 - (0.7034 - 0.0041 * cosB_2) * cosB_2) * cosB_2;
double a4 = (0.25 + 0.00253 * cosB_2) * cosB_2 - 0.04167;
double a6 = (0.166 * cosB_2 - 0.084) * cosB_2;
double a3 = (0.3333333 + 0.001123 * cosB_2) * cosB_2 - 0.1666667;
double a5 = 0.00878 - (0.1702 - 0.20382 * cosB_2) * cosB_2;
//計算高斯平面座標值
double x = 6367452.1328 * B - (a0 - (0.5 + (a4 + a6 * ll) * ll) * ll * N) * cosB * sinB;
double y = (1 + (a3 + a5 * ll) * ll) * l * N * cosB + 500000;
double[] xy = new double[2];
xy[0] = x;
xy[1] = y;
return xy;
}這段程式碼只適用於IAG75(即西安80)下的高斯投影,其他的座標系下的投影需要修改下引數。
總結
至此,左右的轉換已經完成。用了大概一週吧(中間有很長一段時間糾結於誤差大的驚人,今天才知道甲方給的測試資料有問題),算是複習了下專業知識。
下載原始碼
使用方法
(補充自2018年4月19日)
程式是用java寫的,封裝成了CoordsTransformer 類。如果要用於C#、Python語言需要自行修改。
// 首先獲取該類的例項
CoordsTransformer coordsTransformer=CoordsTransformer.getInstance();
// 然後獲取執行結果
double[] resutls=coordsTransformer.fromCgcs2Xian80(119.8774232,28.44428546,112.66);
如果資料量比較多的話,後面這句可以放在一個迴圈裡面。