Spark GraphX學習筆記
概述
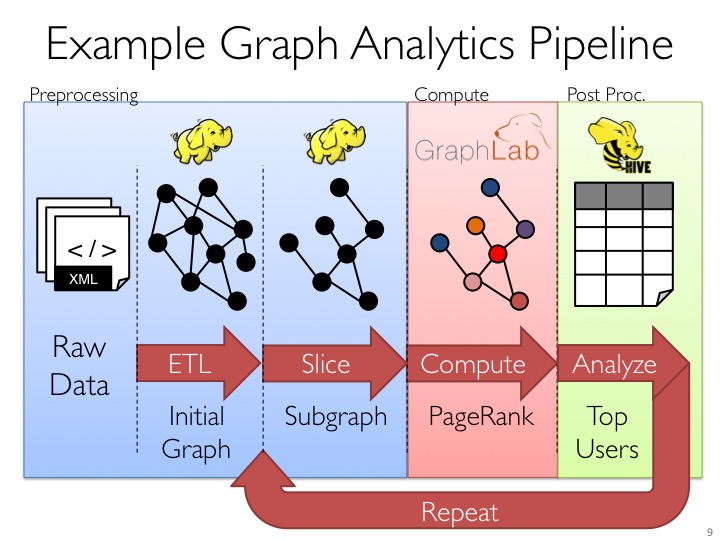
- GraphX是 Spark中用於圖(如Web-Graphs and Social Networks)和圖平行計算(如 PageRank and Collaborative Filtering)的API,可以認為是GraphLab(C++)和Pregel(C++)在Spark(Scala)上的重寫及優化,跟其他分散式 圖計算框架相比,GraphX最大的貢獻是,在Spark之上提供一站式資料解決方案,可以方便且高效地完成圖計算的一整套流水作業。
- Graphx是Spark生態中的非常重要的元件,融合了圖並行以及資料並行的優勢,雖然在單純的計算機段的效能相比不如GraphLab等計算框架,但是如果從整個圖處理流水線的視角(圖構建,圖合併,最終結果的查詢)看,那麼效能就非常具有競爭性了。
圖計算應用場景
“圖計算”是以“圖論”為基礎的對現實世界的一種“圖”結構的抽象表達,以及在這種資料結構上的計算模式。通常,在圖計算中,基本的資料結構表達就是:G = (V,E,D) V = vertex (頂點或者節點) E = edge (邊) D = data (權重)。
圖資料結構很好的表達了資料之間的關聯性,因此,很多應用中出現的問題都可以抽象成圖來表示,以圖論的思想或者以圖為基礎建立模型來解決問題。
下面是一些圖計算的應用場景:
PageRank讓連結來”投票”
基於GraphX的社群發現演算法FastUnfolding分散式實現
http://bbs.pinggu.org/thread-3614747-1-1.html
社交網路分析
如基於Louvian社群發現的新浪微博社交網路分析
社交網路最適合用圖來表達和計算了,圖的“頂點”表示社交中的人,“邊”表示人與人之間的關係。
基於三角形計數的關係衡量
基於隨機遊走的使用者屬性傳播
推薦應用
如淘寶推薦商品,騰訊推薦好友等等(同樣是基於社交網路這個大資料,可以很好構建一張大圖)
淘寶應用
度分佈、二跳鄰居數、連通圖、多圖合併、能量傳播模型
所有的關係都可以從“圖”的角度來看待和處理,但到底一個關係的價值多大?健康與否?適合用於什麼場景?
快刀初試:Spark GraphX在淘寶的實踐
http://www.csdn.net/article/2014-08-07/2821097
Spark中圖的建立及圖的基本操作
圖的構建
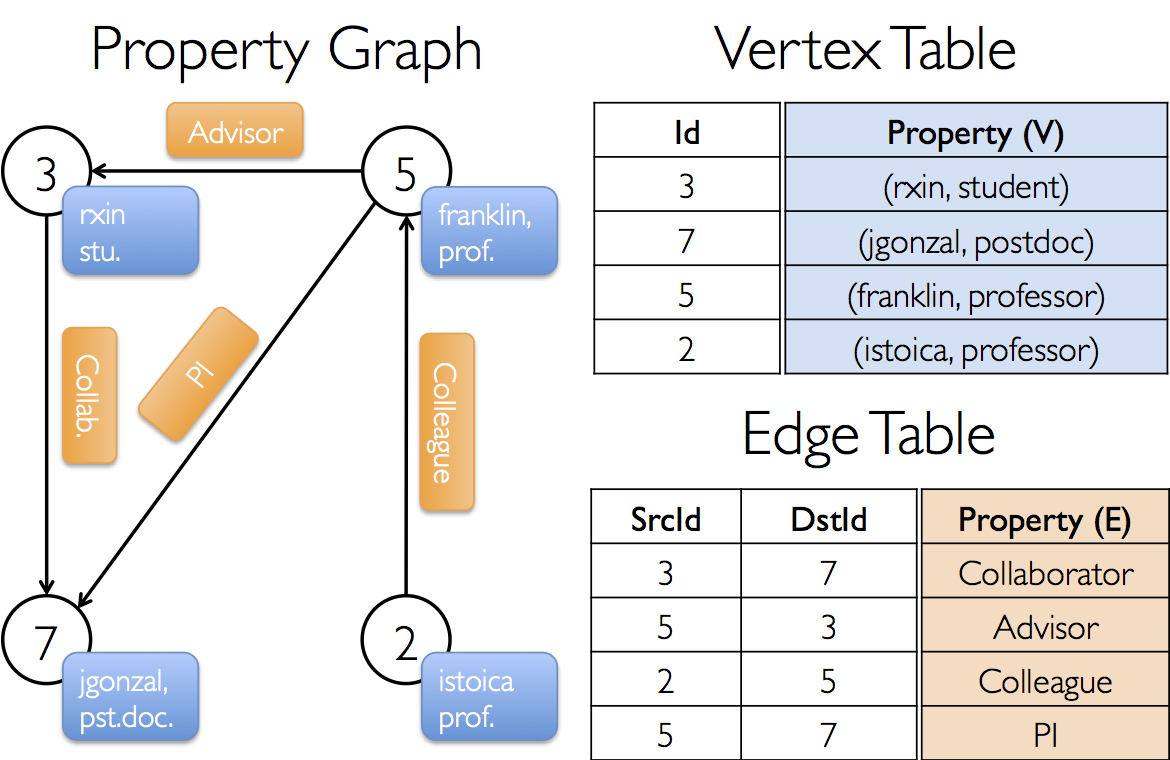
首先利用“頂點”和“邊”RDD建立一個簡單的屬性圖,通過這個例子,瞭解完整的GraphX圖構建的基本流程。
如下圖所示,頂點的屬性包含使用者的姓名和職業,帶標註的邊表示不同使用者之間的關係。
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.spark._
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD
object myGraphX {
def main(args:Array[String]){
// Create the context
val sparkConf = new SparkConf().setAppName("myGraphPractice").setMaster("local[2]")
val sc=new SparkContext(sparkConf)
// 頂點RDD[頂點的id,頂點的屬性值]
val users: RDD[(VertexId, (String, String))] =
sc.parallelize(Array((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")),
(5L, ("franklin", "prof")), (2L, ("istoica", "prof"))))
// 邊RDD[起始點id,終點id,邊的屬性(邊的標註,邊的權重等)]
val relationships: RDD[Edge[String]] =
sc.parallelize(Array(Edge(3L, 7L, "collab"), Edge(5L, 3L, "advisor"),
Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi")))
// 預設(缺失)使用者
//Define a default user in case there are relationship with missing user
val defaultUser = ("John Doe", "Missing")
//使用RDDs建立一個Graph(有許多建立Graph的資料來源和方法,後面會詳細介紹)
val graph = Graph(users, relationships, defaultUser)
}
}上面是一個簡單的例子,說明如何建立一個屬性圖,那麼建立一個圖主要有哪些方法呢?我們先看圖的定義:
object Graph {
def apply[VD, ED](
vertices: RDD[(VertexId, VD)],
edges: RDD[Edge[ED]],
defaultVertexAttr: VD = null)
: Graph[VD, ED]
def fromEdges[VD, ED](
edges: RDD[Edge[ED]],
defaultValue: VD): Graph[VD, ED]
def fromEdgeTuples[VD](
rawEdges: RDD[(VertexId, VertexId)],
defaultValue: VD,
uniqueEdges: Option[PartitionStrategy] = None): Graph[VD, Int]
} 由上面的定義我們可以看到,GraphX主要有三種方法可以建立圖:
(1)在構造圖的時候,會自動使用apply方法,因此前面那個例子中實際上就是使用apply方法。相當於Java/C++語言的建構函式。有三個引數,分別是:vertices: RDD[(VertexId, VD)], edges: RDD[Edge[ED]], defaultVertexAttr: VD = null),前兩個必須有,最後一個可選擇。“頂點“和”邊“的RDD來自不同的資料來源,與Spark中其他RDD的建立並沒有區別。
這裡再舉讀取檔案,產生RDD,然後利用RDD建立圖的例子:
(1)讀取檔案,建立頂點和邊的RRD,然後利用RDD建立屬性圖
//讀入資料檔案
val articles: RDD[String] = sc.textFile("E:/data/graphx/graphx-wiki-vertices.txt")
val links: RDD[String] = sc.textFile("E:/data/graphx/graphx-wiki-edges.txt")
//裝載“頂點”和“邊”RDD
val vertices = articles.map { line =>
val fields = line.split('\t')
(fields(0).toLong, fields(1))
}//注意第一列為vertexId,必須為Long,第二列為頂點屬性,可以為任意型別,包括Map等序列。
val edges = links.map { line =>
val fields = line.split('\t')
Edge(fields(0).toLong, fields(1).toLong, 1L)//起始點ID必須為Long,最後一個是屬性,可以為任意型別
}
//建立圖
val graph = Graph(vertices, edges, "").persist()//自動使用apply方法建立圖(2)Graph.fromEdges方法:這種方法相對而言最為簡單,只是由”邊”RDD建立圖,由邊RDD中出現所有“頂點”(無論是起始點src還是終點dst)自動產生頂點vertextId,頂點的屬性將被設定為一個預設值。
Graph.fromEdges allows creating a graph from only an RDD of edges, automatically creating any vertices mentioned by edges and assigning them the default value.
舉例如下:
//讀入資料檔案
val records: RDD[String] = sc.textFile("/microblogPCU/microblogPCU/follower_followee")
//微博資料:000000261066,郜振博585,3044070630,redashuaicheng,1929305865,1994,229,3472,male,first
// 第三列是粉絲Id:3044070630,第五列是使用者Id:1929305865
val followers=records.map {case x => val fields=x.split(",")
Edge(fields(2).toLong, fields(4).toLong,1L )
}
val graph=Graph.fromEdges(followers, 1L)(3)Graph.fromEdgeTuples方法
Graph.fromEdgeTuples allows creating a graph from only an RDD of edge tuples, assigning the edges the value 1, and automatically creating any vertices mentioned by edges and assigning them the default value. It also supports deduplicating the edges; to deduplicate, pass Some of a PartitionStrategy as the uniqueEdges parameter (for example, uniqueEdges = Some(PartitionStrategy.RandomVertexCut)). A partition strategy is necessary to colocate identical edges on the same partition so they can be deduplicated.
除了三種方法,還可以用GraphLoader構建圖。如下面GraphLoader.edgeListFile:
(4)GraphLoader.edgeListFile建立圖的基本結構,然後Join屬性
(a)首先建立圖的基本結構:
利用GraphLoader.edgeListFile函式從邊List檔案中建立圖的基本結構(所有“頂點”+“邊”),且頂點和邊的屬性都預設為1。
object GraphLoader {
def edgeListFile(
sc: SparkContext,
path: String,
canonicalOrientation: Boolean = false,
minEdgePartitions: Int = 1)
: Graph[Int, Int]
}使用方法如下:
val graph=GraphLoader.edgeListFile(sc, "/data/graphx/followers.txt")
//檔案的格式如下:
//2 1
//4 1
//1 2 依次為第一個頂點和第二個頂點(b)然後讀取屬性檔案,獲得RDD後和(1)中得到的基本結構圖join在一起,就可以組合成完整的屬性圖。
三種檢視及操作
Spark中圖有以下三種檢視可以訪問,分別通過graph.vertices,graph.edges,graph.triplets來訪問。
在Scala語言中,可以用case語句進行形式簡單、功能強大的模式匹配
//假設graph頂點屬性(String,Int)-(name,age),邊有一個權重(int)
val graph: Graph[(String, Int), Int] = Graph(vertexRDD, edgeRDD)
用case匹配可以很方便訪問頂點和邊的屬性及id
graph.vertices.map{
case (id,(name,age))=>//利用case進行匹配
(age,name)//可以在這裡加上自己想要的任何轉換
}
graph.edges.map{
case Edge(srcid,dstid,weight)=>//利用case進行匹配
(dstid,weight*0.01)//可以在這裡加上自己想要的任何轉換
}
也可以通過下標訪問
graph.vertices.map{
v=>(v._1,v._2._1,v._2._2)//v._1,v._2._1,v._2._2分別對應Id,name,age
}
graph.edges.map {
e=>(e.attr,e.srcId,e.dstId)
}
graph.triplets.map{
triplet=>(triplet.srcAttr._1,triplet.dstAttr._2,triplet.srcId,triplet.dstId)
}可以不用graph.vertices先提取頂點再map的方法,也可以通過graph.mapVertices直接對頂點進行map,返回是相同結構的另一個Graph,訪問屬性的方法和上述方法是一模一樣的。如下:
graph.mapVertices{
case (id,(name,age))=>//利用case進行匹配
(age,name)//可以在這裡加上自己想要的任何轉換
}
graph.mapEdges(e=>(e.attr,e.srcId,e.dstId))
graph.mapTriplets(triplet=>(triplet.srcAttr._1))Spark GraphX中的圖的函式大全
/** Summary of the functionality in the property graph */
class Graph[VD, ED] {
// Information about the Graph
//圖的基本資訊統計
===================================================================
val numEdges: Long
val numVertices: Long
val inDegrees: VertexRDD[Int]
val outDegrees: VertexRDD[Int]
val degrees: VertexRDD[Int]
// Views of the graph as collections
// 圖的三種檢視
=============================================================
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
val triplets: RDD[EdgeTriplet[VD, ED]]
// Functions for caching graphs ==================================================================
def persist(newLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED]
def cache(): Graph[VD, ED]
def unpersistVertices(blocking: Boolean = true): Graph[VD, ED]
// Change the partitioning heuristic ============================================================
def partitionBy(partitionStrategy: PartitionStrategy): Graph[VD, ED]
// Transform vertex and edge attributes
// 基本的轉換操作
==========================================================
def mapVertices[VD2](map: (VertexID, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
def mapTriplets[ED2](map: (PartitionID, Iterator[EdgeTriplet[VD, ED]]) => Iterator[ED2])
: Graph[VD, ED2]
// Modify the graph structure
//圖的結構操作(僅給出四種基本的操作,子圖提取是比較重要的操作)
====================================================================
def reverse: Graph[VD, ED]
def subgraph(
epred: EdgeTriplet[VD,ED] => Boolean = (x => true),
vpred: (VertexID, VD) => Boolean = ((v, d) => true))
: Graph[VD, ED]
def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]
def groupEdges(merge: (ED, ED) => ED): Graph[VD, ED]
// Join RDDs with the graph
// 兩種聚合方式,可以完成各種圖的聚合操作 ======================================================================
def joinVertices[U](table: RDD[(VertexID, U)])(mapFunc: (VertexID, VD, U) => VD): Graph[VD, ED]
def outerJoinVertices[U, VD2](other: RDD[(VertexID, U)])
(mapFunc: (VertexID, VD, Option[U]) => VD2)
// Aggregate information about adjacent triplets
//圖的鄰邊資訊聚合,collectNeighborIds都是效率不高的操作,優先使用aggregateMessages,這也是GraphX最重要的操作之一。
=================================================
def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexID]]
def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[Array[(VertexID, VD)]]
def aggregateMessages[Msg: ClassTag](
sendMsg: EdgeContext[VD, ED, Msg] => Unit,
mergeMsg: (Msg, Msg) => Msg,
tripletFields: TripletFields = TripletFields.All)
: VertexRDD[A]
// Iterative graph-parallel computation ==========================================================
def pregel[A](initialMsg: A, maxIterations: Int, activeDirection: EdgeDirection)(
vprog: (VertexID, VD, A) => VD,
sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexID,A)],
mergeMsg: (A, A) => A)
: Graph[VD, ED]
// Basic graph algorithms
//圖的演算法API(目前給出了三類四個API) ========================================================================
def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double]
def connectedComponents(): Graph[VertexID, ED]
def triangleCount(): Graph[Int, ED]
def stronglyConnectedComponents(numIter: Int): Graph[VertexID, ED]
}結構操作
Structural Operators
Spark2.0版本中,僅僅有四種最基本的結構操作,未來將開發更多的結構操作。
class Graph[VD, ED] {
def reverse: Graph[VD, ED]
def subgraph(epred: EdgeTriplet[VD,ED] => Boolean,
vpred: (VertexId, VD) => Boolean): Graph[VD, ED]
def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]
def groupEdges(merge: (ED, ED) => ED): Graph[VD,ED]
}子圖subgraph
子圖(subgraph)是圖論的基本概念之一。子圖是指節點集和邊集分別是某一圖的節點集的子集和邊集的子集的圖。
Spark API–subgraph利用EdgeTriplet(epred)或/和頂點(vpred)滿足一定條件,來提取子圖。利用這個操作可以使頂點和邊被限制在感興趣的範圍內,比如刪除失效的連結。
The subgraph operator takes vertex and edge predicates and returns the graph containing only the vertices that satisfy the vertex predicate (evaluate to true) and edges that satisfy the edge predicate and connect vertices that satisfy the vertex predicate. The subgraph operator can be used in number of situations to restrict the graph to the vertices and edges of interest or eliminate broken links. For example in the following code we remove broken links:
//假設graph有如下的頂點和邊 頂點RDD(id,(name,age) 邊上有一個Int權重(屬性)
(4,(David,42))(6,(Fran,50))(2,(Bob,27)) (1,(Alice,28))(3,(Charlie,65))(5,(Ed,55))
Edge(5,3,8)Edge(2,1,7)Edge(3,2,4) Edge(5,6,3)Edge(3,6,3)
//可以使用以下三種操作方法獲取滿足條件的子圖
//方法1,對頂點進行操作
val subGraph1=graph.subgraph(vpred=(id,attr)=>attr._2>30)
//vpred=(id,attr)=>attr._2>30 頂點vpred第二個屬性(age)>30歲
subGraph1.vertices.foreach(print)
println
subGraph1.edges.foreach {print}
println
輸出結果:
頂點:(4,(David,42))(6,(Fran,50))(3,(Charlie,65))(5,(Ed,55))
邊:Edge(3,6,3)Edge(5,3,8)Edge(5,6,3)
//方法2--對EdgeTriplet進行操作
val subGraph2=graph.subgraph(epred=>epred.attr>2)
//epred(邊)的屬性(權重)大於2
輸出結果:
頂點:(4,(David,42))(6,(Fran,50))(2,(Bob,27))(1,(Alice,28)) (3,(Charlie,65))(5,(Ed,55))
邊:Edge(5,3,8)Edge(5,6,3)Edge(2,1,7)Edge(3,2,4) Edge(3,6,3)
//也可以定義如下的操作
val subGraph2=graph.subgraph(epred=>pred.srcAttr._2<epred.dstAttr._2))
//起始頂點的年齡小於終點頂點年齡
頂點:1,(Alice,28))(4,(David,42))(3,(Charlie,65))(6,(Fran,50)) (2,(Bob,27))(5,(Ed,55))
邊 :Edge(5,3,8)Edge(2,1,7)Edge(2,4,2)
//方法3--對頂點和邊Triplet兩種同時操作“,”號隔開epred和vpred
val subGraph3=graph.subgraph(epred=>epred.attr>3,vpred=(id,attr)=>attr._2>30)
輸出結果:
頂點:(3,(Charlie,65))(5,(Ed,55))(4,(David,42))(6,(Fran,50))
邊:Edge(5,3,8)圖的基本資訊統計-度計算
度分佈:這是一個圖最基礎和重要的指標。度分佈檢測的目的,主要是瞭解圖中“超級節點”的個數和規模,以及所有節點度的分佈曲線。超級節點的存在對各種傳播演算法都會有重大的影響(不論是正面助力還是反面阻力),因此要預先對這些資料量有個預估。藉助GraphX最基本的圖資訊介面degrees: VertexRDD[Int](包括inDegrees和outDegrees),這個指標可以輕鬆計算出來,並進行各種各樣的統計(摘自《快刀初試:Spark GraphX在淘寶的實踐》。
//-----------------度的Reduce,統計度的最大值-----------------
def max(a:(VertexId,Int),b:(VertexId,Int)):(VertexId,Int)={
if (a._2>b._2) a else b }
val totalDegree=graph.degrees.reduce((a,b)=>max(a, b))
val inDegree=graph.inDegrees.reduce((a,b)=>max(a,b))
val outDegree=graph.outDegrees.reduce((a,b)=>max(a,b))
print("max total Degree = "+totalDegree)
print("max in Degree = "+inDegree)
print("max out Degree = "+outDegree)
//小技巧:如何知道a和b的型別為(VertexId,Int)?
//當你敲完graph.degrees.reduce((a,b)=>,再將滑鼠點到a和b上檢視,
//就會發現a和b是(VertexId,Int),當然reduce後的返回值也是(VertexId,Int)
//這樣就很清楚自己該如何定義max函數了
//平均度
val sumOfDegree=graph.degrees.map(x=>(x._2.toLong)).reduce((a,b)=>a+b)
val meanDegree=sumOfDegree.toDouble/graph.vertices.count().toDouble
print("meanDegree "+meanDegree)
println
//------------------使用RDD自帶的統計函式進行度分佈分析--------
//度的統計分析
//最大,最小
val degree2=graph.degrees.map(a=>(a._2,a._1))
//graph.degrees是VertexRDD[Int],即(VertexID,Int)。
//通過上面map調換成map(a=>(a._2,a._1)),即RDD[(Int,VetexId)]
//這樣下面就可以將度(Int)當作鍵值(key)來操作了,
//包括下面的min,max,sortByKey,top等等,因為這些函式都是對第一個值也就是key操作的
//max degree
print("max degree = " + (degree2.max()._2,degree2.max()._1))
println
//min degree
print("min degree =" +(degree2.min()._2,degree2.min()._1))
println
//top(N) degree"超級節點"
print("top 3 degrees:\n")
degree2.sortByKey(true, 1).top(3).foreach(x=>print(x._2,x._1))
println
/*輸出結果:
* max degree = (2,4)//(Vetext,degree)
* min degree =(1,2)
* top 3 degrees:
* (2,4)(5,3)(3,3)
*/ 相鄰聚合—訊息聚合
相鄰聚合(Neighborhood Aggregation)
圖分析任務的一個關鍵步驟是彙總每個頂點附近的資訊。例如我們可能想知道每個使用者的追隨者的數量或者每個使用者的追隨者的平均年齡。許多迭代圖演算法(如PageRank,最短路徑和連通體) 多次聚合相鄰頂點的屬性。
聚合訊息(aggregateMessages)
GraphX中的核心聚合操作是 aggregateMessages,它主要功能是向鄰邊發訊息,合併鄰邊收到的訊息,返回messageRDD。這個操作將使用者定義的sendMsg函式應用到圖的每個邊三元組(edge triplet),然後應用mergeMsg函式在其目的頂點聚合這些訊息。
class Graph[VD, ED] {
def aggregateMessages[Msg: ClassTag](
sendMsg: EdgeContext[VD, ED, Msg] => Unit,//(1)--sendMsg:向鄰邊發訊息,相當與MR中的Map函式
mergeMsg: (Msg, Msg) => Msg,//(2)--mergeMsg:合併鄰邊收到的訊息,相當於Reduce函式
tripletFields: TripletFields = TripletFields.All)//(3)可選項,TripletFields.Src/Dst/All
: VertexRDD[Msg]//(4)--返回messageRDD
}(1)sendMsg:
將sendMsg函式看做map-reduce過程中的map函式,向鄰邊發訊息,應用到圖的每個邊三元組(edge triplet),即函式的左側為每個邊三元組(edge triplet)。
The user defined sendMsg function takes an EdgeContext, which exposes the source and destination attributes along with the edge attribute and functions (sendToSrc, and sendToDst) to send messages to the source and destination attributes. Think of sendMsg as the map function in map-reduce.
//關鍵資料結構EdgeContext原始碼解析
package org.apache.spark.graphx
/**
* Represents an edge along with its neighboring vertices and allows sending messages along the
* edge. Used in [[Graph#aggregateMessages]].
*/
abstract class EdgeContext[VD, ED, A] {//三個型別分別是:頂點、邊、自定義傳送訊息的型別(返回值的型別)
/** The vertex id of the edge's source vertex. */
def srcId: VertexId
/** The vertex id of the edge's destination vertex. */
def dstId: VertexId
/** The vertex attribute of the edge's source vertex. */
def srcAttr: VD
/** The vertex attribute of the edge's destination vertex. */
def dstAttr: VD
/** The attribute associated with the edge. */
def attr: ED
/** Sends a message to the source vertex. */
def sendToSrc(msg: A): Unit
/** Sends a message to the destination vertex. */
def sendToDst(msg: A): Unit
/** Converts the edge and vertex properties into an [[EdgeTriplet]] for convenience. */
def toEdgeTriplet: EdgeTriplet[VD, ED] = {
val et = new EdgeTriplet[VD, ED]
et.srcId = srcId
et.srcAttr = srcAttr
et.dstId = dstId
et.dstAttr = dstAttr
et.attr = attr
et
}
}(2)mergeMsg :
使用者自定義的mergeMsg函式指定兩個訊息到相同的頂點並儲存為一個訊息。可以將mergeMsg函式看做map-reduce過程中的reduce函式。
The user defined mergeMsg function takes two messages destined to the same vertex and yields a single message. Think of mergeMsg as the reduce function in map-reduce.
這裡寫程式碼片(3)TripletFields可選項
它指出哪些資料將被訪問(源頂點特徵,目的頂點特徵或者兩者同時,即有三種可選擇的值:TripletFields.Src,TripletFieldsDst,TripletFields.All。
因此這個引數的作用是通知GraphX僅僅只需要EdgeContext的一部分參與計算,是一個優化的連線策略。例如,如果我們想計算每個使用者的追隨者的平均年齡,我們僅僅只需要源欄位。 所以我們用TripletFields.Src表示我們僅僅只需要源欄位。
takes an optional tripletsFields which indicates what data is accessed in the EdgeContext (i.e., the source vertex attribute but not the destination vertex attribute). The possible options for the tripletsFields are defined in TripletFields and the default value is TripletFields.All which indicates that the user defined sendMsg function may access any of the fields in the EdgeContext. The tripletFields argument can be used to notify GraphX that only part of the EdgeContext will be needed allowing GraphX to select an optimized join strategy. For example if we are computing the average age of the followers of each user we would only require the source field and so we would use TripletFields.Src to indicate that we only require the source field
(4)返回值:
The aggregateMessages operator returns a VertexRDD[Msg] containing the aggregate message (of type Msg) destined to each vertex. Vertices that did not receive a message are not included in the returned VertexRDD.
//假設已經定義好如下圖:
//頂點:[Id,(name,age)]
//(4,(David,18))(1,(Alice,28))(6,(Fran,40))(3,(Charlie,30))(2,(Bob,70))(5,Ed,55))
//邊:Edge(4,2,2)Edge(2,1,7)Edge(4,5,8)Edge(2,4,2)Edge(5,6,3)Edge(3,2,4)
// Edge(6,1,2)Edge(3,6,3)Edge(6,2,8)Edge(4,1,1)Edge(6,4,3)(4,(2,110))
//定義一個相鄰聚合,統計比自己年紀大的粉絲數(count)及其平均年齡(totalAge/count)
val olderFollowers=graph.aggregateMessages[(Int,Int)](
//方括號內的元組(Int,Int)是函式返回值的型別,也就是Reduce函式(mergeMsg )右側得到的值(count,totalAge)
triplet=> {
if(triplet.srcAttr._2>triplet.dstAttr._2){
triplet.sendToDst((1,triplet.srcAttr._2))
}
},//(1)--函式左側是邊三元組,也就是對邊三元組進行操作,有兩種傳送方式sendToSrc和 sendToDst
(a,b)=>(a._1+b._1,a._2+b._2),//(2)相當於Reduce函式,a,b各代表一個元組(count,Age)
//對count和Age不斷相加(reduce),最終得到總的count和totalAge
TripletFields.All)//(3)可選項,TripletFields.All/Src/Dst
olderFollowers.collect().foreach(println)
輸出結果:
(4,(2,110))//頂點Id=4的使用者,有2個年齡比自己大的粉絲,同年齡是110歲
(6,(1,55))
(1,(2,110))
//計算平均年齡
val averageOfOlderFollowers=olderFollowers.mapValues((id,value)=>value match{
case (count,totalAge) =>(count,totalAge/count)//由於不是所有頂點都有結果,所以用match-case語句
})
averageOfOlderFollowers.foreach(print)
輸出結果:
(1,(2,55))(4,(2,55))(6,(1,55))//Id=1的使用者,有2個粉絲,平均年齡是55歲
Spark Join連線操作
許多情況下,需要將圖與外部獲取的RDDs進行連線。比如將一個額外的屬性新增到一個已經存在的圖上,或者將頂點屬性從一個圖匯出到另一圖中(在自己編寫圖計算API 時,往往需要多次進行aggregateMessages和Join操作,因此這兩個操作可以說是Graphx中非常重要的操作,需要非常熟練地掌握,在本文最後的例項中,有更多的例子可供學習)
In many cases it is necessary to join data from external collections (RDDs) with graphs. For example, we might have extra user properties that we want to merge with an existing graph or we might want to pull vertex properties from one graph into another.
有兩個join API可供使用:
class Graph[VD, ED] {
def joinVertices[U](table: RDD[(VertexId, U)])(map: (VertexId, VD, U) => VD)
: Graph[VD, ED]
def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2)
: Graph[VD2, ED]
}兩個連線方式差別非常大。下面分別來說明
joinVertices連線
返回值的型別就是graph頂點屬性的型別,不能新增,也不可以減少(即不能改變原始graph頂點屬性型別和個數)。
經常會遇到這樣的情形,”一個額外的費用(extraCost)增加到老的費用(oldCost)中”,oldCost為graph的頂點屬性值,extraCost來自外部RDD,這時候就要用到joinVertices:
extraCosts: RDD[(VertexID, Double)]//額外的費用
graph:Graph[Double,Long]//oldCost
val totlCosts = graph.joinVertices(extraCosts)( (id, oldCost, extraCost) => oldCost + extraCost)
//extraCost和oldCost資料型別一致,且返回時無需改變原始graph頂點屬性的型別。
再舉一個例子:
// 假設graph的頂點如下[id,(user_name,initial_energy)]
//(6,(Fran,0))(2,(Bob,3))(4,(David,3))(3,(Charlie,1))(1,(Alice,2))(5,(Ed,2))
// graph邊如下:
//Edge(2,1,1)Edge(2,4,1)Edge(4,1,1)Edge(5,2,1)Edge(5,3,1)Edge(5,6,1)Edge(3,2,1)Edge(3,6,1)
// 每個src向dst鄰居傳送生命值為2能量
val energys=graph.aggregateMessages[Long](
triplet=>triplet.sendToDst(2), (a,b)=>a+b)
// 輸出結果:
// (1,4)(4,2)(3,2)(6,4)(2,4)
val energys_name=graph.joinVertices(energys){
case(id,(name,initialEnergy),energy)=>(name,initialEnergy+energy)
}
//輸出結果:
// (3,(Charlie,3))(1,(Alice,6))(5,(Ed,2))(4,(David,5))(6,(Fran,4))(2,(Bob,7))
// 我們注意到,如果energys:RDD中沒有graph某些頂點對應的值,則graph不進行任何改變,如(5,(Ed,2))。 從上面的例子我們知道:將外部RDD joinvertices到graph中,對應於graph某些頂點,RDD中無對應的屬性,則保留graph原有屬性值不進行任何改變。
而與之相反的是另一種情況,對應於graph某一些頂點,RDD中的值不止一個,這種情況下將只有一個值在join時起作用。可以先使用aggregateUsingIndex的進行reduce操作,然後再join graph。
val nonUniqueCosts: RDD[(VertexID, Double)]
val uniqueCosts: VertexRDD[Double] =
graph.vertices.aggregateUsingIndex(nonUnique, (a,b) => a + b)
val joinedGraph = graph.joinVertices(uniqueCosts)(
(id, oldCost, extraCost) => oldCost + extraCost)If the RDD contains more than one value for a given vertex only one will be used. It is therefore recommended that the input RDD be made unique using the following which will also pre-index the resulting values to substantially accelerate the subsequent join.
(2)outerJoinVertices
更為常用,使用起來也更加自由的是outerJoinVertices,至於為什麼後面會詳細分析。
The more general outerJoinVertices behaves similarly to joinVertices except that the user defined map function is applied to all vertices and can change the vertex property type. Because not all vertices may have a matching value in the input RDD the map function takes an Option type.
從下面函式的定義我們注意到,與前面JoinVertices不同之處在於map函式右側型別是VD2,不再是VD,因此不受原圖graph頂點屬性型別VD的限制,在outerJoinVertices中使用者可以隨意定義自己想要的返回型別,從而可以完全改變圖的頂點屬性值的型別和屬性的個數。
class Graph[VD, ED] {
def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2)
: Graph[VD2, ED]
}用上面例子中的graph和energys資料:
val graph_energy_total=graph.outerJoinVertices(energys){
case(id,(name,initialEnergy),Some(energy))=>(name,initialEnergy,energy,initialEnergy+energy)
case(id,(name,initialEnergy),None)=>(name,initialEnergy,0,initialEnergy)
}
// 輸出結果:
// (3,(Charlie,1,2,3))(1,(Alice,2,4,6))(5,(Ed,2,0,2))
// (4,(David,3,2,5))(6,(Fran,0,4,4))(2,(Bob,3,4,7))Spark Scala幾個語法問題
大多數語言都有一個特殊的關鍵字或者物件來表示一個物件引用的是“無”,在Java,它是null。
Scala鼓勵你在變數和函式返回值可能不會引用任何值的時候使用Option型別。在沒有值的時候,使用None,這是Option的一個子類。如果有值可以引用,就使用Some來包含這個值。Some也是Option的子類。
通過模式匹配分離可選值,如果匹配的值是Some的話,將Some裡的值抽出賦給x變數。舉一個綜合的例子:
def showCapital(x: Option[String]) = x match {
case Some(s) => s
case None => "?"
}
/*
Option用法:Scala推薦使用Option型別來代表一些可選值。使用Option型別,讀者一眼就可以看出這種型別的值可能為None。
如上面:x: Option[String])引數,就是因為引數可能是String,也可能為null,這樣程式不會在為null時丟擲異常
*/Spark中,經常使用在map中使用case語句進行匹配None和Some,再舉一個例子
//假設graph.Vertice:(id,(name,weight))如下:
//(4,(David,Some(2)))(3,(Charlie,Some(2)))(6,(Fran,Some(4)))(2,(Bob,Some(4)))(1,(Alice,Some(4)))(5,(Ed,None))
//id=5時,weight=None,其他的為Some
val weights=graph.vertices.map{
case (id,(name,Some(weight)))=>(id,weight)
case (id,(name,None))=>(id,0)
}
weights.foreach(print)
println
//輸出結果如下(id,weight):
//(3,2)(6,4)(2,4)(4,2)(1,4)(5,0)在上面的例子中,其實我們也可以選用另外一個方法,getOrElse。這個方法在這個Option是Some的例項時返回對應的值,而在是None的例項時返函式引數。
上面例子可以用下面的語句獲得同樣的結果:
val weights=graph.vertices.map{
attr=>(attr._1,attr._2._2.getOrElse(0))
//如果attr._2._2!=None,返回attr._2._2(weight)的值,
//否則(即attr._2._2==None),返回自己設定的函式引數(0)
}
//輸出同樣的結果:
//(id,weight)
(4,2)(6,4)(2,4)(3,2)(1,4)(5,0)
圖演算法工具包
1.數三角形
TriangleCount主要用途之一是用於社群發現,如下圖所示:

例如說在微博上你關注的人也互相關注,大家的關注關係中就會有很多三角形,這說明社群很強很穩定,大家的聯絡都比較緊密;如果說只是你一個人關注很多人,這說明你的社交群體是非常小的。(摘自《大資料Spark企業級實戰》一書)
graph.triangleCount().vertices.foreach(x=>print(x+"\n"))
/*輸出結果
* (1,1)//頂點1有1個三角形
* (3,2)//頂點3有2個三角形
* (5,2)
* (4,1)
* (6,1)
* (2,2)
*/2.連通圖
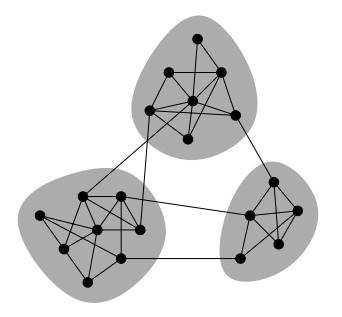
現實生活中存在各種各樣的網路,諸如人際關係網、交易網、運輸網等等。對這些網路進行社群發現具有極大的意義,如在人際關係網中,可以發現出具有不同興趣、背景的社會團體,方便進行不同的宣傳策略;在交易網中,不同的社群代表不同購買力的客戶群體,方便運營為他們推薦合適的商品;在資金網路中,社群有可能是潛在的洗錢團伙、刷鑽聯盟,方便安全部門進行相應處理;在相似店鋪網路中,社群發現可以檢測出商幫、價格聯盟等,對商家進行指導等等。總的來看,社群發現在各種具體的網路中都能有重點的應用場景,圖1展示了基於圖的拓撲結構進行社群發現的例子。
檢測連通圖可以弄清一個圖有幾個連通部分及每個連通部分有多少頂點。這樣可以將一個大圖分割為多個小圖,並去掉零碎的連通部分,從而可以在多個小子圖上進行更加精細的操作。目前,GraphX提供了ConnectedComponents和StronglyConnected-Components演算法,使用它們可以快速計算出相應的連通圖。
連通圖可以進一步演化變成社群發現演算法,而該演算法優劣的評判標準之一,是計算模組的Q值,來檢視所謂的modularity情況。
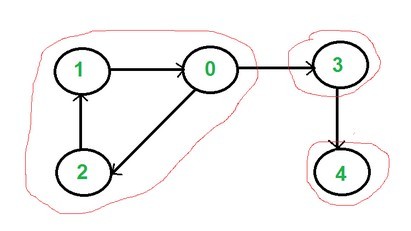
如果一個有向圖中的每對頂點都可以從通過路徑可達,那麼就稱這個圖是強連通的。一個 strongly connected component就是一個有向圖中最大的強連通子圖。下圖中就有三個強連通子圖:
//連通圖
def connectedComponents(maxIterations: Int): Graph[VertexId, ED]
def connectedComponents(): Graph[VertexId, ED]
//強連通圖
//numIter:the maximum number of iterations to run for
def stronglyConnectedComponents(numIter: Int): Graph[VertexId, ED]//連通圖計算社群發現
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.log4j.{Level, Logger}
import org.apache.spark._
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD
object myConnectComponent {
def main(args:Array[String]){
val sparkConf = new SparkConf().setAppName("myGraphPractice").setMaster("local[2]")
val sc=new SparkContext(sparkConf)
//遮蔽日誌
Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)
Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)
val graph=GraphLoader.edgeListFile(sc, "/spark-2.0.0-bin-hadoop2.6/data/graphx/followers.txt")
graph.vertices.foreach(print)
println
graph.edges.foreach(print)
println
val cc=graph.connectedComponents().vertices
cc.foreach(print)
println
/*輸出結果
* (VertexId,cc)
* (4,1)(1,1)(6,1)(3,1)(2,1)(7,1)
*/
//強連通圖-stronglyConnectedComponents
val maxIterations=10//the maximum number of iterations to run for
val cc2=graph.stronglyConnectedComponents(maxIterations).vertices
cc2.foreach(print)
println
val path2="/spark-2.0.0-bin-hadoop2.6/data/graphx/users.txt"
val users=sc