資料結構與演算法13-哈夫曼樹及其應用
赫夫曼樹及其應用
最基本的壓縮編碼方法----赫夫曼編碼
定義與原理
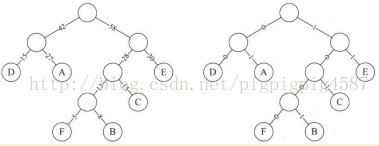
我們先把這兩棵二叉樹簡化成葉子結點帶權的二叉樹(注:樹結點間的邊相差的數叫做權Weight)
從樹中一個結點到另一個結點之間的分支構成兩個結點之間的路徑,路徑上的分支數目稱做路徑長度。
如:二叉樹a中,根結點到結點D的路徑長度就為4,二叉樹b中根結點到結點D的路徑長度為2。
如圖所示:其中A表示不及格、B表示及格、C表示中等、D表示良好、E表示優秀。每個葉子的分支線上的數字就是五個級別分制的成績所佔的百分比。
樹的路徑長度就是從樹根到每一結點的路徑長度之和。
二叉樹a的樹路徑長度就為1+1+2+2+3+3+4+4=20
二叉樹b的樹路徑長度就為1+2+3+3+2+1+2+2=16
若將樹中結點賦給一個有著某種含義的數值,則這個數值稱為該結點的權。結點的帶權路徑長度為:從根結點到該結點之間的路徑長度與該結點的權的乘積。
如果考慮到帶權的結點,結點的帶權的路徑長度為從該結點到樹根之間的路徑長度與結點上權的乘積。樹的帶權路徑長度為樹中所有葉子結點的帶權路徑長度之和。
假設有n個權值{W1,W2,…Wn},構造一棵有n個葉子結點的二叉樹,每個葉子結點帶權Wk,每個葉子的路徑長度為lk,我們通常記作,帶權路徑長度WPL最小的二叉樹稱做赫夫曼樹(最優二叉樹)。
有了上面的定義,我們來計算一下,上圖中這兩棵二叉的WPL
二叉樹a
WPL=5x1+15x2+40x3+30x4+10x4=315
二叉樹b
WPL=5x3+15x3+40x2+30x2+10x2=220
這樣的結果意味著什麼呢?如果我們現在有10000個學生的百分制成績需要計算五級分製成績,用二叉樹a判斷方法,需要做31500次比較,而二叉樹b的判斷只需要22000次比較,差不多少了三分之一量,在效能上提高不是一點點。
現在的問題就是,二叉樹b這樣的樹是如何構造出來的,這樣的二叉樹是不是就是最估赫夫曼樹呢? 赫夫曼給出如下解決方案
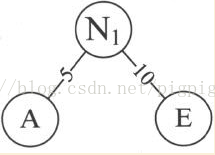
1. 先把有權值的葉子結點按照從小到大的順序排列成一個有序序列,即A5,E10,B15,D30,C40。
2. 取頭兩個最小權值的結點作為一個新節點N1的兩個子結點,注意相對較小的是左孩子,這裡就是A為N1的左孩子,E為N1的右孩子。如圖
新結點的權值 為兩個葉子權值的和5+10=15
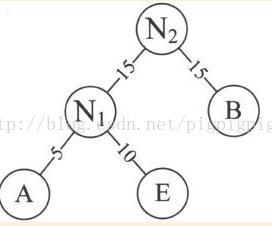
3. 將N1替換A與E,插入有序序列中,保持從小到大排列即:N115,B15,D30,C40
4. 重複步驟2.將N1與B作為一個新節點N2的兩個結點。N2權值=15+15=30。
5. 將N2替換N1與B,插入有序序列中,保持從小到大排列。即N230,D30,C40.
6. 重複步驟2。將N2與D作為一個新節點N3的兩個子結點。N3權值=30+30=60
7. 將N3替換N2與D,插入有序序列中,保持從小到大排列。C40,N360。
8. 重複步驟2。與C與N3作為一個新節點T的兩個子結點,由於T即是根結點,完成赫夫曼樹的構造
此時的下圖的二叉樹的帶權路徑長度
WPL=40x1+30x2+15x3+10x4+5x4=205。比之前的b二叉樹的WPL值還少15。顯然此時構造出來的二叉樹才是最優的赫夫曼樹。
不過現實總是比理想要複雜得多,上圖雖然是二叉樹,但由於每次判斷都要兩次比較
如根結點:就是a<80&& a>=70。總體效能上,反而不如b二叉樹效能高。當然這並不是討論的重點。
通過上例我們可以對構造赫夫曼樹的赫夫曼演算法描述。
1. 根據給定的n個權值{W1,W2,…,WN}構成的n棵二叉樹集合F={T1,T2,...Tn},其中每棵二叉樹Ti中只有一個帶權為Wi的根結點,其左右子樹均為空
2. 在F中選取兩棵根結點可能會最小的樹作為左右子樹構造一棵新的二叉樹,且置新的二叉樹的根結點的權值為其左右子樹上根結點的權值之和。
3. 在F中刪除這兩棵樹,同時將新得到的二叉樹加入F中。
4. 重複2和3步驟,直到F只含一棵樹為止。這棵樹便是赫夫曼樹。
赫夫曼編碼
比如我們有一段文字要傳輸給別人,顯然用二進位制的數字(0 ,1)來表示是很自然的想法。我們現在這段文字只有六個字母ABCDEF,那麼我們可以用相應的二進位制資料表示,如下:
這樣真正傳輸的資料就是編碼後的“000001010011100101”對方接收時可以按照3位一分來譯碼。如果一篇文章很長,這樣的二進位制串也將非常可怕。而且事實上,不管是英文、中文或是其它語言,字母或漢字的出現頻率是不相同的,比如英語中的幾個母音字母,中文的“的了有在”等漢字都是頻率極高。
假設六個字母的頻率為A 27,B 8,C 15,D 15,E 30,F 5合起來正好是100%。那就意味著,我們完全可以重新按照赫夫曼樹來規劃它們。我們將左圖的可能會顯示。右圖為將權值左分支改為0,右分支改為1後的赫夫曼樹。
此時,我們對這六個字母用其從樹根到葉子所經過路徑的0或1來編碼,可以得到這樣的定義。
原串二進位制串是30個字元,新編碼二進位制串是25個字元。也就說是資料被壓縮了,節約了大約17%的儲存或傳輸成本。隨著字元的增加和多字元權重的不同,這種壓縮會更加顯出其優勢。
編碼中非0即1,長短不等的話其實是容易混淆的,所以若要設計長短不等的編碼,則必須是任一字元的編碼都不是另一個字元的編碼字首,這種編碼稱做字首編碼。
可這不能方便我們去解碼,因此在解碼時,還是要用到赫夫曼樹,即傳送方和接收方必須要約定好同樣的赫夫曼編碼規則。當我們接收時由原來的哈夫曼樹可知。1001得到的字母是B 01得到的字母是A
結論:
一般地,設需要編碼的字符集為{d1,d2…dn},各個字元在電文中出現的次數或頻率集合為{w1,w2,…w3},以d1,d2,…dn作為葉子結點,以w1,w2,…wn作為相應葉子結點的權值來構造一棵赫夫曼樹。規定赫夫曼樹左分支代表0,右分支代表1,則從根結點到葉子結點所經過的路徑分支組成的0和1的序列便為該結點對應字元的編碼。這就是赫夫曼編碼。