資料結構課程設計-哈夫曼樹及其應用
阿新 • • 發佈:2019-01-06
題目:假設用於通訊的電文由字符集{a,b,c,d,e,f,g,h,}中的字母構成,這8個字母在電文中出現的 頻率分別為:
{0.19, 0.21, 0.02, 0.03, 0.06, 0.07, 0.1, 0.32}.
要求:畫出哈夫曼樹。
我從課本上面摘抄了一個題目,題目大概是上面這樣的,我們這裡只是詳細的說明一下哈弗曼樹要怎麼構建。借用一下這個題目。
分析:我們這裡直接將小數整數化,容易看出大小來。
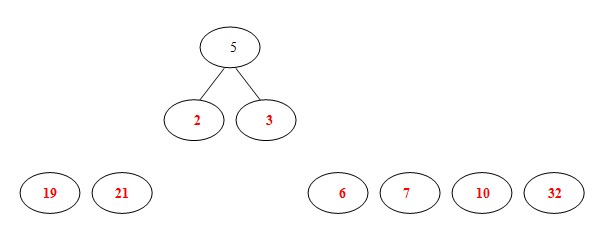
(1)8個結點的權值大小如下:
(2)從19,21,2,3,6,7,10,32中選擇兩個權小結點。選中2,3。同時算出這兩個結點的和5。
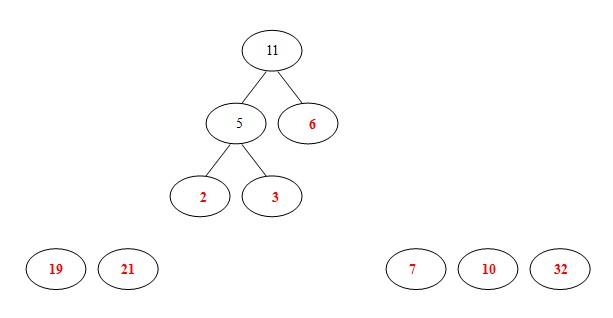
(3)從19,21,6,7,10,32,5中選出兩個權小結點。選中5,6。同時計算出它們的和11。
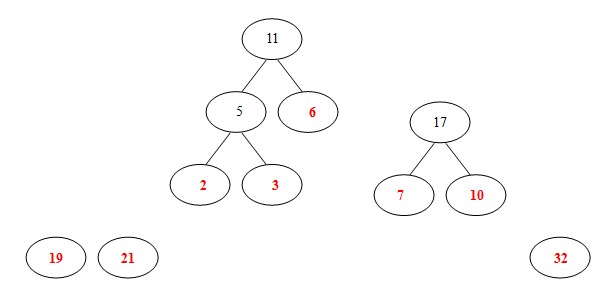
(4)從19,21,7,10,32,11中選出兩個權小結點。選中7,10。同時計算出它們的和17。
注:這時選出的兩個數字都不是原來的二叉樹裡面的結點,所以要另外開一棵二叉樹。
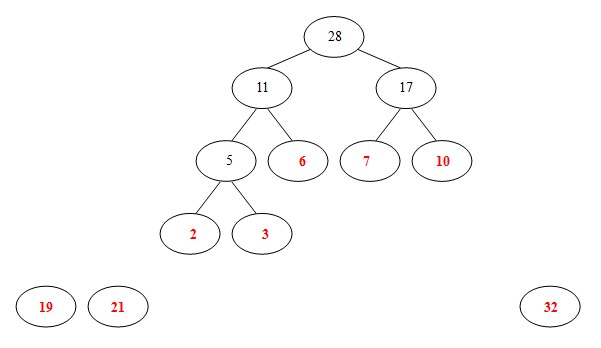
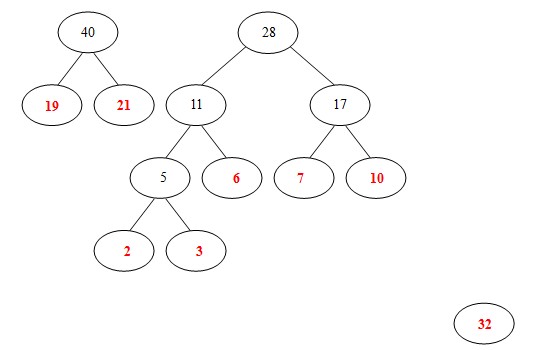
(5)從19,21,32,11,17中選出兩個權小結點。選中11,17。同時計算出它們的和28。
(6)從19,21,32,28中選出兩個權小結點。選中19,21。同時計算出它們的和40。 另起一顆二叉樹。
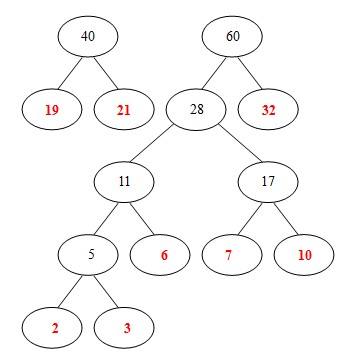
(7)從32,28, 40中選出兩個權小結點。選中28,32。同時計算出它們的和60。
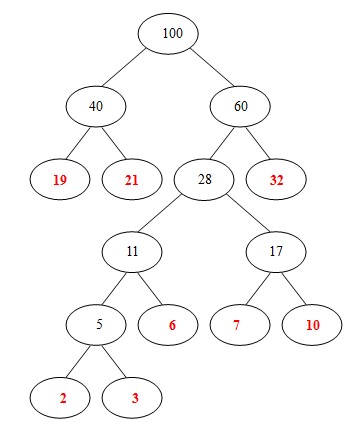
(7)從 40, 60中選出兩個權小結點。選中40,60。同時計算出它們的和100。 好了,此時哈夫曼樹已經構建好了。
ps:上次做作業的時候,我構造哈弗曼樹就是一直從剩下的結點裡面找權值最小的,然後新增上去,而沒有考慮構造出來的"和"權值的大小問題。導致哈夫曼樹構造錯誤!
哈夫曼編碼及譯碼的實現:
[cpp] view plain copy print?- #include<stdio.h>
- #include<string.h>
- #include<stdlib.h>
- //樹結點定義
- typedefstruct
- {
- int weight;
- int parent;
- int lchild;
-
int rchild;
- }HTNode,*HuffmanTree;
- staticchar N[100];//用於儲存正文
- //哈弗曼編碼,char型二級指標
- typedefchar **HuffmanCode;
- //封裝最小權結點和次小權結點
- typedefstruct
- {
- int s1;
- int s2;
- }MinCode;
- //函式宣告
- void Error(char *message);
- HuffmanCode HuffmanCoding(HuffmanTree &HT,HuffmanCode HC,int *w,int n);
- MinCode Select(HuffmanTree HT,int n);
- //當輸入1個結點時的錯誤提示
- void Error(char *message)
- {
- fprintf(stderr,"Error:%s\n",message);
- exit(1);
- }
- //構造哈夫曼樹HT,編碼存放在HC中,w為權值,n為結點個數
- HuffmanCode HuffmanCoding(HuffmanTree &HT,HuffmanCode HC,int *w,int n)
- {
- int i,s1=0,s2=0;
- HuffmanTree p;
- char *cd;
- int f,c,start,m;
- MinCode min;
- if(n<=1)
- {
- Error("Code too small!");//只有一個結點不進行編碼,直接exit(1)退出。非return,如果return 會造成main函式HT[i]無值
- }
- m=2*n-1;//哈弗曼編碼需要開闢的結點大小為2n-1
- HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));//開闢哈夫曼樹結點空間 m+1 。為了對應關係,我們第0個空間不用。
- //初始化n個葉子結點,w[0] = 0,main函式已賦值
- for(p=HT,i=0;i<=n;i++,p++,w++)
- {
- p->weight=*w;
- p->parent=0;
- p->lchild=0;
- p->rchild=0;
- }
- //將n-1個非葉子結點的初始化
- for(;i<=m;i++,p++)
- {
- p->weight=0;
- p->parent=0;
- p->lchild=0;
- p->rchild=0;
- }
- //構造哈夫曼樹
- for(i=n+1;i<=m;i++)
- {
- min=Select(HT,i-1);//找出最小和次小的兩個結點
- s1=min.s1 ; //最小結點下標
- s2=min.s2;//次小結點下標
- HT[s1].parent=i;
- HT[s2].parent=i;
- HT[i].lchild=s1;
- HT[i].rchild=s2;
- HT[i].weight=HT[s1].weight+HT[s2].weight;//賦權和
- }
- //列印哈弗曼樹
- printf("HT List:\n");
- printf("Number\t\tweight\t\tparent\t\tlchild\t\trchild\n");
- for(i=1;i<=m;i++)
- {
- printf("%d\t\t%d\t\t%d\t\t%d\t\t%d\t\n",i,HT[i].weight,HT[i].parent,HT[i].lchild,HT[i].rchild);
- }
- //從葉子結點到根節點求每個字元的哈弗曼編碼
- HC=(HuffmanCode)malloc((n+1)*sizeof(char *));
- cd=(char *)malloc(n*sizeof(char *));//為哈弗曼編碼動態分配空間
- cd[n-1]='\0';//如:3個結點編碼最長為2。cd[3-1] = '\0';
- //求葉子結點的哈弗曼編碼
- for(i=1;i<=n;i++)
- {
- start=n-1;
- //定義左子樹為0,右子樹為1
- /*
- 從最下面的1號節點開始往頂部編碼(逆序存放),然後編碼2號節點,3號......
- */
- for(c=i,f=HT[i].parent; f!=0; c=f,f=HT[f].parent)
- {
- if(HT[f].lchild==c)
- cd[--start]='0';
- else
- cd[--start]='1';
- }
- //為第i個字元分配編碼空間
- HC[i]=(char *)malloc((n-start)*sizeof(char *));
- //將當前求出結點的哈弗曼編碼複製到HC
- strcpy(HC[i],&cd[start]);
- }
- free(cd);
- return HC;
- }
- MinCode Select(HuffmanTree HT,int n)
- {
- int min,secmin;
- int temp = 0;
- int i,s1,s2,tempi = 0;
- MinCode code ;
- s1=1;
- s2=1;
- min = 66666;//足夠大
- //找出權值weight最小的結點,下標儲存在s1中
- for(i=1;i<=n;i++)
- {
- if(HT[i].weight<min && HT[i].parent==0)
- {
- min=HT[i].weight;
- s1=i;
- }
- }
- secmin = 66666;//足夠大
- //找出權值weight次小的結點,下標儲存在s2中
- for(i=1;i<=n;i++)
- {
- if((HT[i].weight<secmin) && (i!=s1) && HT[i].parent==0)
- {
- secmin=HT[i].weight;
- s2=i;
- }
- }
- //放進封裝中
- code.s1=s1;
- code.s2=s2;
- return code;
- }
- void HuffmanTranslateCoding(HuffmanTree HT, int n,char