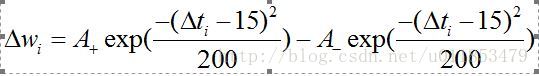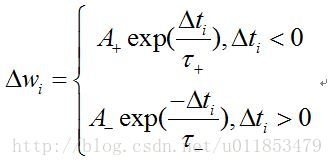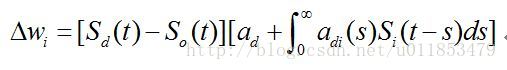脈衝神經元模型

傳統的人工神經元模型主要包含兩個功能，一是對前一層神經元傳遞的訊號計算加權和，二是採用一個非線性啟用函式輸出訊號。 前者用於模仿生物神經元之間傳遞資訊的方式，後者用來提高神經網路的非線性計算能力。相比於人工神經元，脈衝神經元則從神經科學的角度出發，對真實的生物神經元進行建模。

Hodgkin-Huxley（ HH）模型

HH模型是一組描述神經元細胞膜的電生理現象的非線性微分方程，直接反映了細胞膜上離子通道的開閉情況。

HH模型所對應的電路圖如圖1-1所示，其中 C 代表脂質雙層(lipid bilayer) 的電容；RNa, RK, Rl分別代表鈉離子通道、 鉀離子通道與漏電通道的電阻（RNa, RK 上的斜箭頭表明其為隨時間變化的變數， 而 R l 則為一個常數）； E l, E Na, E K 分別代表由於膜內外電離子濃度差別所導致的漏電平衡電壓、鈉離子平衡電壓、鉀離子平衡電壓；膜電壓V代表神經膜內外的電壓差，可以通過HH模型的模擬來得到V隨時間變化的曲線。

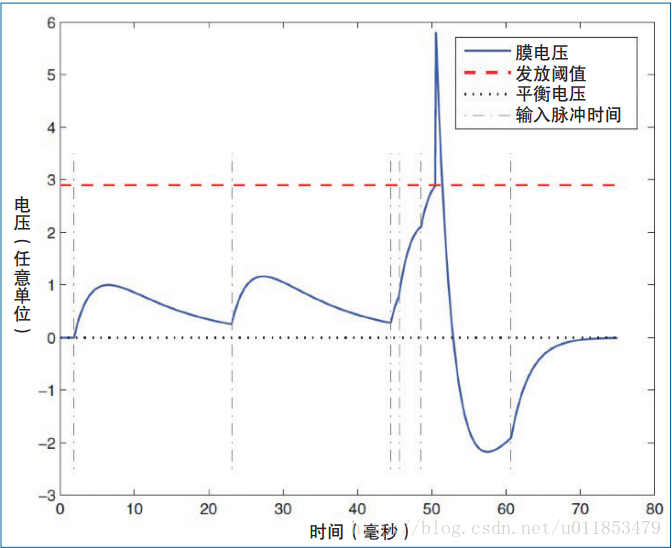
神經元的膜電壓變化，如圖1-2所示。

圖中共有6個輸入脈衝（垂直虛線所示），每個脈衝觸發膜電壓V的快速上升。如果輸入脈衝之間的時間間隔較長（例如在1ms與22ms到達的2個脈衝之間，由於漏電通道的作用，沒有新的輸入脈衝），膜電壓V就會隨著時間逐漸降低至平衡電壓El。如果有多個輸入脈衝在短時間內連續到達（例如在45~50ms 之間的3 個脈衝），那麼膜電壓V會上升至發放閾值Vth（紅色水平虛線所示） 而觸發一個輸出脈衝。之後V被重置為低於平衡電壓El的Vreset，然後逐漸回升至平衡電壓El。神經元的行為與輸入的時間特性密切相關，一組脈衝如果在短時間內連續到達，可以觸發神經元的脈衝；但是同樣數量的一組脈衝如果在較長時間內分散到達，那麼膜電壓的漏電效應便不會產生脈衝。

HH模型精確地描繪出膜電壓的生物特性，能夠很好地與生物神經元的電生理實驗結果相吻合，但是運算量較高，難以實現大規模神經網路的實時模擬。

Leaky Integrate and Fire(LIF)模型

為了解決HH模型運算量的問題，許多學者提出了一系列的簡化模型。LIF模型將細胞膜的電特性看成電阻和電容的組合。

Izhikevich模型

HH模型精確度高，但運算量大。LIF模型運算量小，但犧牲了精確度。Izhikevich模型結合了兩者的優勢，生物精確性接近HH模型，運算複雜度接近LIF模型。

神經脈衝序列

在完成神經元的建模之後，需要對神經元傳遞的資訊進行編碼，一種主流的方法是通過神經元的放電頻率來傳遞資訊。在大腦皮層，連續動作電位的時序非常沒有規律。一種觀點認為這種無規律的內部脈衝間隔反映了一種隨機過程，因此瞬時放電頻率可以通過求解大量神經元的響應均值來估計。另一種觀點認為這種無規律的現象可能是由突觸前神經元活動的精確巧合所形成的，反映了一種高頻寬的資訊傳遞通路。本文主要基於第一種觀點，用隨機過程的方法生成脈衝序列。

瞬時放電頻率

神經元的響應函式有一系列的脈衝函式所構成，如公式所示。

ρ(t)=∑ki=1δ(t−ti)

其中，k表示某個脈衝序列中的脈衝數， 表示每個脈衝到達的時間。由脈衝函式的性質可得，在時間間隔 內，脈衝數可通過公式來計算。

n=∫t2t1ρ(t)dt

因此瞬時放電頻率可定義為神經元響應函式的期望，如公式所示。

r(t)=dn(t)dt=E(ρ(t))

根據概率學統計理論，以某一小段時間間隔內的神經元響應函式的均值來作為放電頻率的估計值，如公式所示。

rM(t)=1M∑Mj=1ρj(t)

齊次泊松過程

假設每個脈衝的生成是相互獨立的，並且瞬時放電頻率是一個常數。設時間段 內含有k個脈衝，那麼在時間段 內含有n個脈衝的概率可由公式表示。

P(n,t1,t2)=k!(k−n)!n!pnqk−n

其中，p=(t2−t1)T，q=1−p 。令k趨於無窮大，同時平均放電頻率 保持不變，得到

P(n,t1,t2)=e−rΔtrΔtnn!

可以看出，上式與泊松分佈的概率密度函式形式相同，進一步說明了脈衝發放過程可用泊松過程來模擬。

泊松脈衝序列的生成

相鄰脈衝間的時間間隔固定

對於齊次泊松過程，在固定時間間隔δt內，產生一個脈衝的概率為

P(n=1)≈rΔt

因此，以泊松模型產生神經脈衝序列的方法如下。選取一個固定的時間間隔，產生一個 區間的符合均勻分佈的隨機數x[i]。對於每一個間隔，如果x[i]≤rΔt ，則發放一個脈衝，否則不產生脈衝。在實踐中，時間間隔必須足夠小，產生的脈衝才會近似符合泊松分佈。

相鄰脈衝見的時間間隔不固定

根據上面的討論，在間隔[t0,t0+τ]內，發放的脈衝數為0的概率為

P(n=0)=e−rτ

因此，在時刻t0+τ之前發放脈衝的概率可表示為

P(τ)=1−e−rτ

那麼，相鄰兩個脈衝之間的等待時間的概率密度分佈可表示為

p(τ)=d(1−e−rτ)dt=re−rτ

由此，產生神經脈衝序列的方法如下。當一個脈衝發放完成之後，從符合指數分佈的隨機數集合中隨機選擇一個數作為下一次發放脈衝需等待的時間。依次類推，便可產生符合泊松模型的神經脈衝序列。

擴充套件

非齊次泊松過程

相較於齊次泊松過程，非齊次泊松模型假設放電頻率是時間的函式 ，更具有一般性。只有間隔 足夠小，那麼在這段時間內，放電頻率仍可以視為常數。上述的理論依然有效。

不應期

根據神經科學理論，神經元在放電之後的短暫時間記憶體在不應期，即對輸入訊號不響應。為了在脈衝序列中模擬這個過程，在神經元放電之後的不應期內將瞬時放電頻率置為0。在不應期結束之後，瞬時放電頻率 在限定時間內逐漸回到原始值。

湧現

神經元在某個時刻會集中性的放電，稱為湧現現象。為了模擬這種現象，設定每個時刻發放的泊松脈衝數不固定，可能包含0，1，或多個脈衝。每個時刻發放的脈衝數符合一定的概率分佈。例如，設x是 上符合均勻分佈的一個隨機數，當x取不同值時，該時刻發放的脈衝數也不同。

脈衝神經網路的訓練方法

人工神經網路主要基於誤差反向傳播（BP）原理進行有監督的訓練，目前取得很好的效果。對於脈衝神經網路而言，神經資訊以脈衝序列的方式儲存，神經元內部狀態變數及誤差函式不再滿足連續可微的性質，因此傳統的人工神經網路學習演算法不能直接應用於脈衝神經神經網路。目前，脈衝神經網路的學習演算法主要有以下幾類。

無監督學習演算法

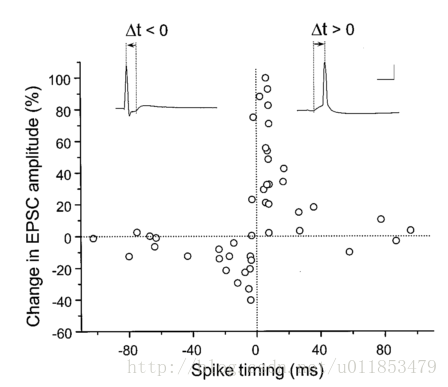
這類演算法從生物可解釋性出發，主要基於赫布法則 (Hebbian Rule)。Hebb在關於神經元間形成突觸的理論中提到，當兩個在位置上臨近的神經元，在放電時間上也臨近的話，他們之間很有可能形成突觸。而突觸前膜和突觸後膜的一對神經元的放電活動（spike train）會進一步影響二者間突觸的強度。這個假說也得到了實驗驗證。華裔科學家蒲慕明和畢國強在大樹海馬區神經元上，通過改變突觸前膜神經元和突觸後膜神經元放電的時間差，來檢驗二者之間突觸強度的變化。實驗結果如圖3-1所示。

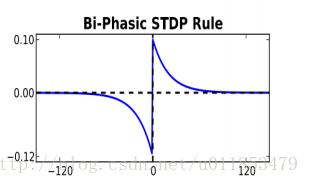
其中，EPSC表示突觸強度。當EPSP(興奮性脈衝)在spike之前產生，突觸強度增強。當EPSP在spike之後產生，突觸強度減弱。這個現象被稱為脈衝序列相關的可塑性（Spike Timing Dependent Plasticity，STDP）。
基於該生物現象，提出了兩種主流的無監督STDP學習演算法。

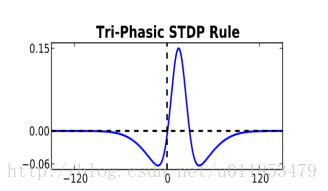
三相STDP

權值更新規則如公式所示。

其中， A+和A− 表示學習率， 表示突觸前脈衝傳到突觸後脈衝所需的時間。函式關係如圖3-2所示。

二相STDP

權值更新規則如公式所示。

其中， τ+和τ− 用來控制電壓下降的速度，被視為時間常數。函式關係如圖3-3所示。

有監督學習演算法

有監督學習演算法依據是否具有生物可解釋性分為兩大類，一種是基於突觸可塑性的監督學習演算法，另外兩種分別是基於梯度下降規則的監督學習演算法和基於脈衝序列卷積的監督學習演算法。

基於突觸可塑性的監督學習演算法

監督Hebbian學習演算法

通過“教師”訊號使突觸後神經元在目標時間內發放脈衝，“教師”訊號可以表示為脈衝發放時間，也可以轉換為神經元的突觸電流形式。在每個學習週期，學習過程由3個脈衝決定，包括2個突觸前脈衝和1個突觸後脈衝。第一個突觸前脈衝表示輸入訊號，第二個突觸前脈衝表示突觸後神經元的目標脈衝，權值的學習規則可表示為

Δw=η(tfo−tfd)

其中，η表示學習率，tfo 和tfd 分別表示突觸後神經元的實際和目標脈衝時間。

遠端監督學習演算法（ReSuMe）

遠端監督方法結合STDP和anti-STDP兩個過程，提出的突觸權值隨時間變化的學習規則為

其中，S