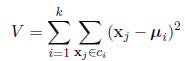最近做的一個東西跟這個相關，本來希望是用深度學習對於沒有標籤的影象資料進行分類，但是通常情況下，深度學習是對有標籤的資料進行學習，目的是用來自動提取特徵，代替傳統的手工提取特徵。因此，比較容易想到，對於無標籤又需要分類的影象資料，可以嘗試先採用聚類來解決.

下面的內容是譯自Jan Erik Solem的《Programming Computer Vision with Python》的第6章，該書已經由朱文濤和袁勇學長對該書進行了翻譯，主要涉及相關程式碼和例項，可以轉至http://yongyuan.name/pcvwithpython/。 我僅對其中第6章的理論進行翻譯，中途穿插自己的理解。

該博文僅供交流學習，如有侵權，請聯絡刪除。

====================================================================

第6章  影象聚類

這一章節主要介紹了幾種聚類方法，顯示瞭如何將其用在聚類影象中從而找到相似圖片的組。聚類可以用於識別，用於將影象資料集進行分類，用於組織和導航。我們也關注將聚類用於影象間的相似度的視覺化。

6.1 K均值聚類（K-meansClustering）

K均值是一個非常簡單的聚類演算法，將輸入資料分到K個類中。K均值是通過迴圈更新類中心的初始估計值來實現的，其步驟如下：

1.初始化類重心ui, I = 1, …k, 可以通過隨機初始化或者使用一些猜測的值；

2.將每一個數據點賦給距離類ci最近的中心；

3.更新中心為賦給某一類的所有資料點的平均值；

4.重複步驟2和3直至收斂。

K均值儘可能地最小化類之間的方差：

其中xj是資料向量。上面的演算法是一個啟發式的提煉演算法，對於大多數的情況是試用的，但是不能夠保證得到的結果是最好的。為了避免找到一個不好的中心的初始化的影響，該演算法通常是使用不同的初始化中心執行幾次。然後從這些結果中選擇具有最小方差V的作為最後的結果。

該演算法的主要缺陷是，類的數目需要提前確定，也就是說，我們必須一開始指定將資料聚成幾類，也就是傳入的引數K。這樣的話，一個不恰當的選擇可能就會導致很差的聚類結果。其優勢是實現起來很簡單，是並行化的，並且對於大範圍的問題不需要任何調整就可以實現很好的結果。

SciPy聚類包

由於該書的例子都是使用python實現，因此需要介紹一些必要的包。

儘管K均值演算法容易實現，但是也不是沒有必要實現一下。SciPy向量量化包sciPy.cluster.vq自帶一個K均值的實現。下面是它如何使用的。

讓我們首先從建立一些二維樣本資料來說明。

這個可以在二維下生成2個正態分佈的類。為了聚類這些點，可以設定k=2執行下面的k聚類：

方差會被返回但是事實上我們不是非常需要，因為SciPy實現計算了幾次執行（預設是20）然後為我們選擇了有著最小方差的一個返回。現在，需要在SciPy包中確認是否每一個數據點都使用向量量化函式被賦值了。

通過檢查code的值，我們可以看到是否存在不正確的賦值。為了視覺化，我們可以將這些點和最後的中心都畫出來。

這裡函式where()是給出每一個類的索引。通過執行程式碼，可以得到下面的結果：

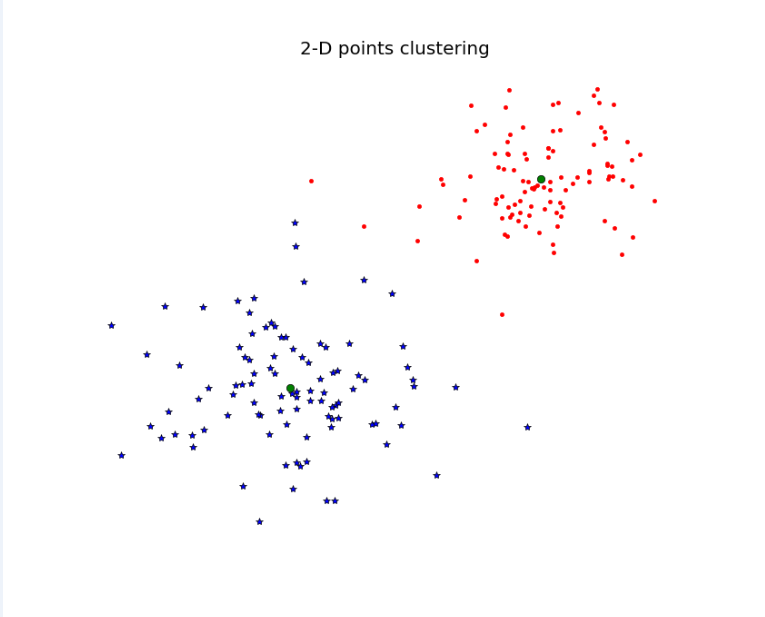
圖1- 2D點的K均值聚類的樣例

這是我重新跑的結果，因為書上的圖不是特別清楚。其中類重心是被標記為綠色的環，預測的類別分別是藍色的星星和紅色的點點。

影象聚類

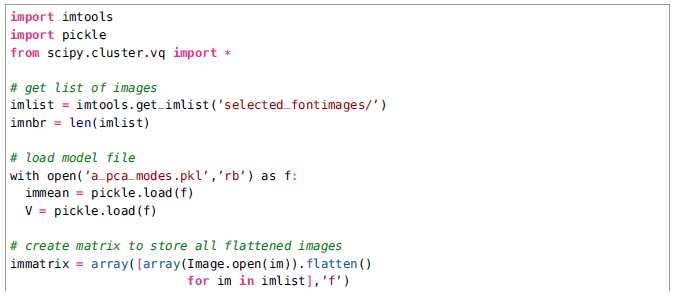
下面我們將K均值演算法運用在書中前面章節提到過的字型影象中。檔案selectedfontimages.zip包含66張從這個字型資料集中提取的影象（這些選擇都是為了在顯示類時容易觀察，另住：這些資料也可以通過最開始提到的連結中下載到）。作為每一個影象的描述向量，我們將會使用對映係數，在對映到先計算好的前40個首要主成分之後。使用pickle載入模型檔案，然後主成分上的影象對映和聚類就可以按照下面的程式碼實現：

跟之前一樣，code包含了對於每一張影象的聚類賦值。在這個例項中，我們令k=4。我們也使用sciPy的whiten()函式將資料進行漂白，歸一化，使得每一個特徵都有單位方差。盡力改變像使用的主成分的數目和k的值這樣的引數為了觀察聚類結果是如何改變的。聚類可以通過下面的程式碼被視覺化：

這裡，我們對每一個類都使用一個單獨的最多顯示40張影象的網格視窗來顯示。我們使用PyLab函式subplot()來定義這個網格。一個例項結果如下。

圖2- 使用40個主成分的字型影象，k=4的K均值聚類

主成分視覺化影象

為了看使用一些主成分的聚類如何實現，我們可以通過在一組主成分方向上基於它們的座標視覺化影象。其中一個方法是通過改變對映得到相關的座標（在這個例子中，V[[0,2]]給出第一個和第三個）而對映到兩個成分上。另外，對映所有的主成分，然後選出你需要的列。

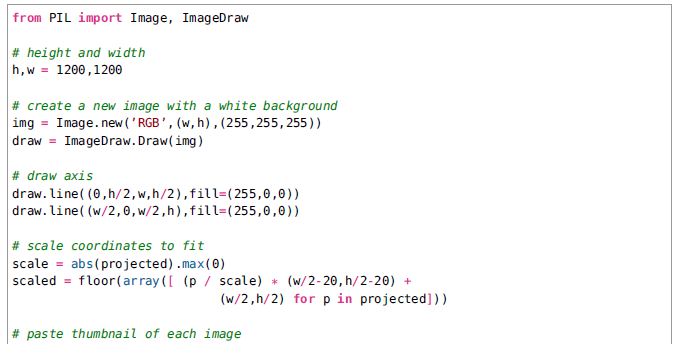
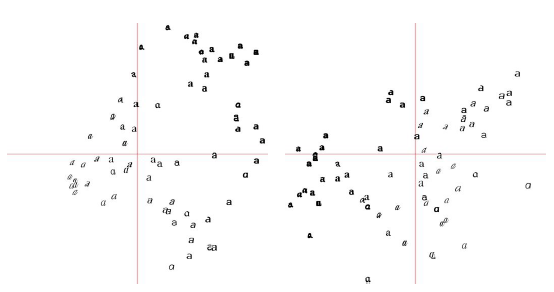
為了視覺化，我們將使用PIL中的ImageDraw。假設你已經有了所有的對映影象和影象列表，下面的程式碼將生成圖3

圖3- 在成對主成分上的字型影象的對映。

左邊是第一和第二個主成分，右邊是第二和第三個

這裡，我們使用了整數和地板整數運算子//，該運算子通過移除小數點後的值返回一個整數畫素位置。

像這樣的圖說明了在40維中影象是如何被分佈的，並且在選擇一個好的描述符時非常有用。已經在這二維對映中的相似的字型影象的分界線可以清晰可見。

畫素聚類

在這一節結束之前，我們將看一個聚類單獨的畫素而不是整個影象的例子。將影象區域（和畫素）分組成有意義的成分叫做影象分割，這也是後面第9章的內容。將K均值演算法簡單的應用到畫素值上是不能夠得出任何有意義的東西的，除非是在非常非常簡單的影象中。更加複雜的類模型（比平均畫素顏色）或者空間一致性是需要來產生更加有用的結果。現在，我們將K均值應用到RGB值上，之後再考慮解決分割問題（章節9.2會有詳細描述）。

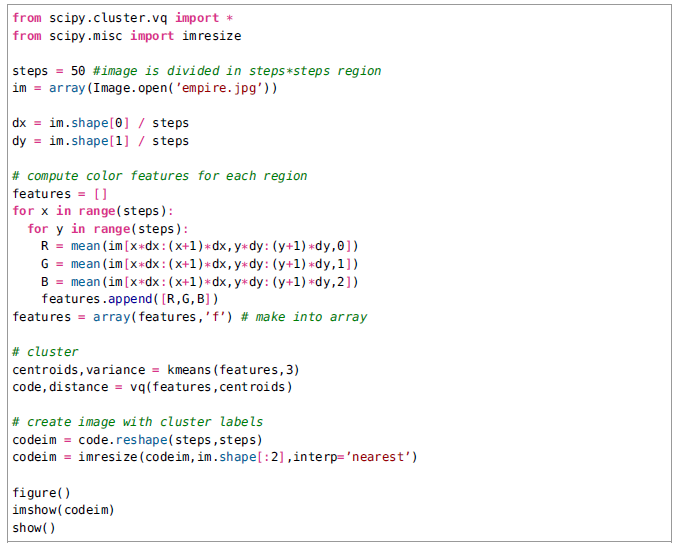
下面的程式碼樣本輸入一張影象，將其減到一個更低的解析度的版本，其中畫素是原始影象區域（大小step * step的正方形網格表示）的平均值，並使用K均值聚類這些區域。

K均值的輸入時一個有著steps * steps行的陣列，每一個包含R，G和B的均值。為了視覺化結果，我們使用SciPy的imresize()函式來顯示在最初影象座標處的steps * steps的影象。引數interp指定使用哪一種插值方式，這裡我們使用最近鄰，這樣我們在類之間的轉換時不需要引入新的畫素值。

圖4顯示了使用50x50和100x100區域用於兩個相對簡單的樣例影象的結果。需要注意的是，K均值標籤（這個情況下是結果影象中的顏色）的順序是任意的。正如你所看到的，儘管下采樣為了只使用一些區域結果也是比較有噪的。沒有空間一致性，也很難分離區域，像下面例子中的男孩和草地。

空間一致性和更好的分離將在之後被處理，與其他的影象分割演算法一起。

圖4-使用K均值給予它們顏色值的畫素聚類。左邊是原始圖片，

中間是k=3和50x50解析度的聚類結果，右邊是k=3和100x100解析度的聚類結果。