最近在遊戲公司實習的過程中需要學習場景管理，這裡就整理了下。

常見場景管理技術

對於一個有很多物體的3D場景來說，渲染這個場景最簡單的方式就是用一個List將這些物體進行儲存，並送入GPU進行渲染。當然，這種做法在效率上來說是相當低下的，因為真正需要渲染的物體應該是視椎體內的物體。除此之外，從裁剪演算法和碰撞檢測等演算法的效率來說，使用這種資料結構也是相當低效的。比較好的方式是使用具有層次結構的空間資料結構儲存待渲染的物體，如BVH（包圍體層次結構）、BSP（二叉空間分割）樹、四叉樹、八叉樹和模糊K-D樹等，在進行空間查詢或者剔除的時候將時間複雜度從O(n)降低到O(logn)。當然，對應的代價是每幀更新的時候，需要更新對應的空間資料結構。

常見場景管理方法

• 多層次包圍盒（BVH）
• 四叉樹
• 八叉樹
• BSP樹
• k-d樹

某些遊戲或引擎的場景管理方法

• quake3：BSP，代表遊戲《雷神之錘》
• unreal engine4：BSP，代表遊戲《天涯明月刀》《虛幻競技場》
• cry engine3：室內BSP，室外不是很清楚，代表遊戲《孤島危機》
• RenderWare：模糊k-d樹，代表遊戲《俠盜獵車手》《仙劍5》
• GameBryo：包圍球層次結構，代表遊戲《上古卷軸：天際》《古劍奇譚》
• Angelica：室外四叉樹，八叉樹，室內不清楚，國產MMO基本都是地形一套管理機制，其他的一套管理機制，代表遊戲《完美國際》《誅仙》《笑傲江湖》

BVH（bounding volume hierarchies，包圍體層次結構）

BV（bounding volume，包圍體）是包含一組物體的空間體，它要比所包含的幾何物體形狀簡單得多，所以在使用包圍體進行碰撞檢測等操作的時候比使用物體本身更快。常見的包圍體有AABB（axis-aligned bounding boxes，軸對齊包圍盒），OBB（oriented bounding boxes，有向包圍盒），以及k-DOP（discrete oriented polytope，離散定向多面體），詳細解釋見維基百科。

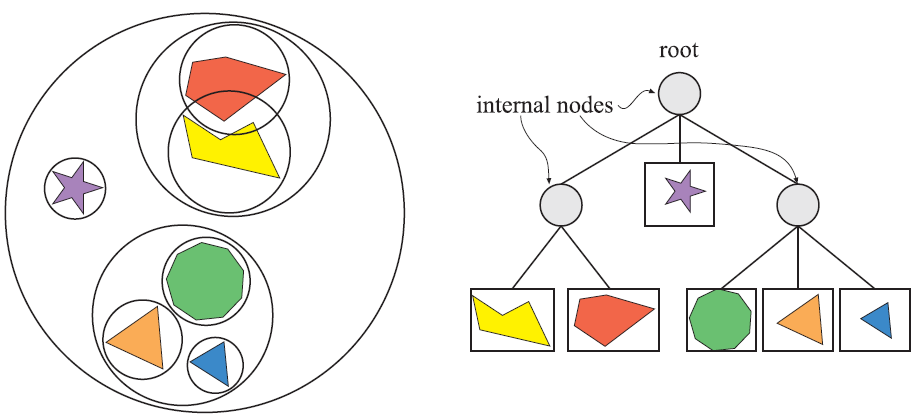
對於三維場景的實時渲染來說，BVH是最常使用的資料結構，例如，BVH經常用於視椎體裁剪。場景以層次樹形結構進行組織，包含一個根節點、內部節點和葉子節點。最高節點是根，沒有父節點；葉子節點儲存著需要繪製的實際幾何體（BVH只能儲存幾何體，實際渲染的物體除了幾何屬性還有其他屬性，一般使用場景圖表示，參看維基百科）。樹中的每個節點，包括葉子節點，都有一個包圍體，可以將其子樹的所有幾何體包圍起來，這就是BVH（包圍體層次結構）名字的來源，圖1為BVH的示例。

在場景中的物體移動的時候，需要對BVH進行更新。如果物體移動以後仍然在原先的包圍體內，則不需要更新；若不在，則刪除這個物體所在節點，並重新計算其父節點的包圍體，然後，從根節點開始，以遞迴形式將這個節點插入這棵樹中。另一種方法則是以遞迴形式增大父節點的包圍體，直到這個包圍體可以包含這個子節點為止。無論使用哪種方法，隨著編輯操作的增多，這棵樹會變得越來越不平衡，效率也會越來越低。

BSP（binary space partitioning，二叉空間分割）樹

BSP樹在1969年由Shumacher首次提出，當時並未想到能成為開發娛樂產品的演算法，但從90年代初BSP樹就已經被用於遊戲行業來改善效能，並使利用地圖中更多細節成為可能。第一個使用該技術的遊戲是Doom，由遊戲行業中的兩位傳奇人物JohnCarmack和John Romero創立。

在計算機圖形學中，BSP樹有兩種不同的形式：分別為軸對齊(axis-aligned)和多邊形對齊(polygon-aligned)。要建立BSP樹，首先用一個平面將空間一分為二，然後將幾何體按類別劃分到這兩個空間中，隨後以遞迴形式反覆進行這個過程。這種樹有一個非常有趣的特性，如果按照一定的方式對樹進行遍歷，那麼會從某個視點將這棵樹包含的幾何體進行排序（對於軸對齊的方式來說，它是粗略的排序；對於多邊形對齊方式來說，它的準確的排序）。在Z-Buffer問世之前，基於多邊形對齊的BSP樹成為3D遊戲進行場景排序的最佳方案。

軸對齊BSP樹

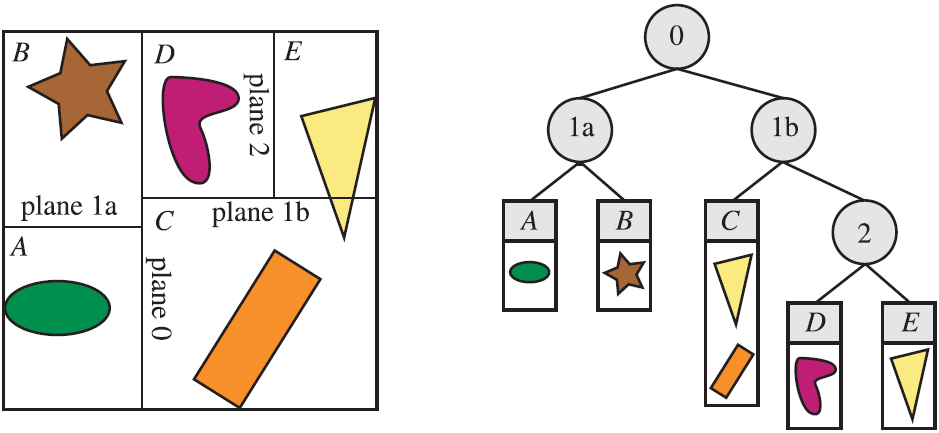
軸對齊BSP樹的建立方式如下：首先，將整個場景包圍在一個AABB中，選取xyz其中一個軸，生成一個與之垂直的平面，將該AABB分為兩個小AABB，然後以遞迴的方式繼續對生成的AABB進行分割，直到樹達到最大深度或AABB中包含的幾何圖元數量低於使用者定義的某個閾值。軸對齊BSP樹的結構如圖2所示。

在分割的時候，有些物體會與分割平面相交，對這些物體有以下幾種處理方法：1）儲存在分割平面所在的節點中，如圖2中的三角形也可以儲存在1b中（圖2採用的是第二種方法）；2）儲存在多個葉子節點，如圖2所示；3）將這個物體由這個平面分為兩個物體。第一種方法效率比較低，比如物體比較小，但是恰好被平面分割，不得不將其存在較高的節點中，所以實際中很少採用這種做法；第二種方法會導致相同的物體被繪製多次，一般使用timestamping方法對其進行改進，即對繪製過的幾何體做一個標記，繪製前對這個標記進行檢查，若已經繪製過，則不再繪製，這種方法使用的比較多；第三種方法由於要對圖元進行分割，所以計算量比較大，而且對於動態物體的渲染不太方便。

分割平面的選取也有多種方法：1）按照xyz-xyz……的順序進行迴圈分割，如果每次都選擇中間位置，則結果和八叉樹一樣。當然，也可以隨意選定位置，BSP樹相對於八叉樹的優勢之一就是平面的位置可以隨意選擇。2）對AABB的最長邊進行分割。3）通過相關演算法（geometric probablity theory）計算出近似最優的分割平面，該分割平面將盡可能少的與幾何體相交。

軸對齊BSP樹具有粗略排序的特徵，對遮擋裁剪（occlusion culling）等演算法具有較好的加速作用。在遮擋裁剪中，如果能夠按照從前往後的順序進行渲染，則可以減少畫素著色器的負擔。使用軸對齊BSP樹，從根節點開始，先遍歷靠近視點一側的所有物體，再遍歷遠離視點的所有物體，對於每個子節點採用這種方式遞迴，則可以做到近似的從前往後進行渲染。由於它沒有對葉子節點內的幾何體進行排序，而且一個物體可能在多個葉子節點中，所以軸對齊BSP樹只是粗略的排序。

多邊形對齊BSP樹

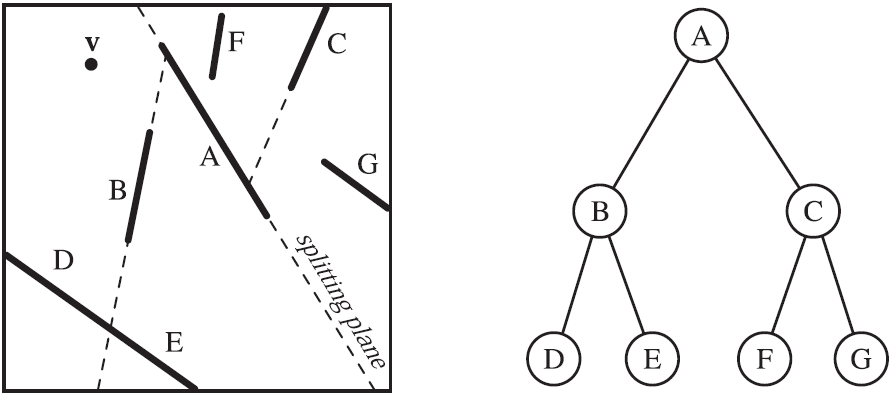
多邊形對齊的BSP樹採用多邊形所在的平面進行空間分割，具體方法如下：在根節點處選取一個多邊形，用這個多邊形所在平面將場景中剩餘的多邊形分為兩組。對於與分割平面相交的多邊形，沿著相交線將這個多邊形分為兩個部分。接下來採用同樣的方式對這些多邊形進行遞迴分割，直到所有的多邊形都在這棵BSP樹中，如圖3所示。

多邊形對齊BSP樹的建立非常耗時，適合靜態場景，它的優點是對於給定視點，可以按照嚴格排序的順序進行遍歷，在沒有Z-Buffer的DOS時代，這種方法是3D遊戲製作中一種很好的方法，著名的FPS遊戲Doom和Quake都使用了這種方法，並且quake裡面還用了一個技巧，用一個二進位制變數的不同位來儲存子節點的索引，將對子節點索引的遞迴演算法改進成了迴圈的演算法，優化了空間複雜度。當然，現在已經不再使用了這種方法（它的好處被Z-Buffer取代，其缺點是隻適用於靜態場景，使用不便）。

PVS和portal技術

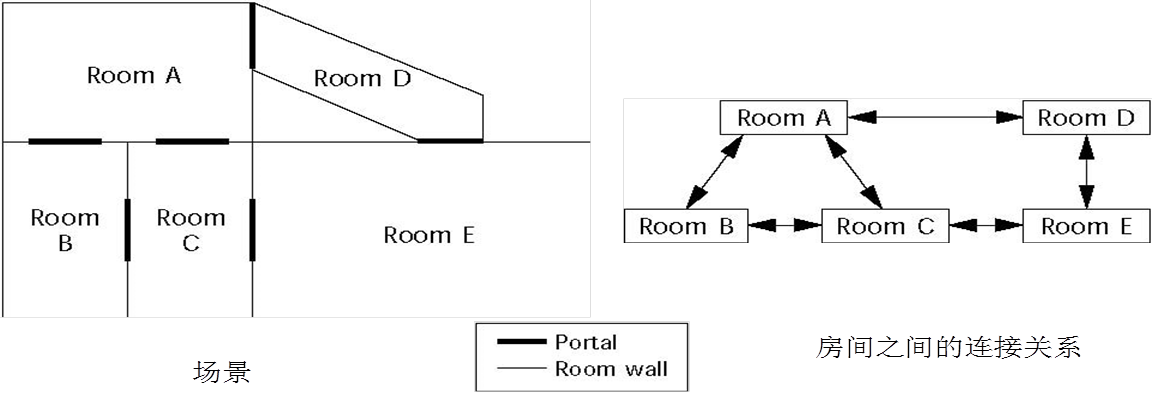
雖然二叉樹已經是非常有效的方法，但是僅僅依靠二叉樹還是不能滿足遊戲的要求，因為現在的遊戲的場景是在是很大很複雜，又很多的物品，按照二叉樹的方法凡是與view frustum 相交的Leaf 必然要送入渲染器，因為view frustum是很大的，所以會有很多的Leaf 與他相交，這就意味著渲染器還是要處理很多的資料，如果你確實能夠看到這麼多的物體，那也沒有辦法，但是通常，比如很多室內的場景，雖然在你的frustum 裡面會由很多物體，但是你真正能夠看到的還是很少的一部分，比如一個封閉的房間。因此被稱為Portal 的技術被引入到遊戲中來，之所以能夠使用Portal 技術，那是因為很多室內場景自身的限制條件所致。我們引入region 的概念，一個region 就是一個相對封閉的空間，比如一個房間，region 與region 之間都是通過Portal（比如門或窗）相連線，因此，如果你處於一個region 當中，你就只能看到這個region 中的物體，如果你能夠看到其他region 中的物體，那麼你一定是通過Portal 看到的，所以處理的過程如下（考慮Portal 是單向的情況，如果兩個region 可以通過一個門相互看到，我就是用兩個單向的Portal）。

valve公司出品的《傳送門》遊戲就很有這種portal技術的味道呢 :)

一個portal引擎雖然能夠提供許多非常好的特性，但是它的結構太複雜。當你使用portal技術來構建一個遊戲引擎時你會發現它存在許多問題，最大的一個問題是在渲染場景的每一幀都需要進行可視性檢測，這會產生大量的多邊形剪下操作，在場景非常複雜的情況下，運算的費用會非常的高，因此需要尋找一種技術來對場景中可視性檢測進行預計算而不是在執行期間進行計算。PVS（Potentially Visible Set）可視性集合，就是為了解決這個問題而出現的一項技術，可以通過對BSP中每一個葉節點設定一個PVS，這個PVS儲存了從第一個葉節點開始看到的葉節點集合，它不僅可以用來幫助加速場景渲染，還可以用來加速場景中光照運算和進行網路優化。PVS是在場景進行預渲染時計算出來的，每一個BSP的葉節點都儲存一個可視節點的集合，當對場景進行渲染時，攝象機所在的葉節點將被渲染，同時保持在PVS中的葉節點也將會被渲染出來，這裡需要一些演算法來避免場景重複渲染，由於今天硬體加速卡的發展，它所提供的硬體Z緩衝的大小已經可以方便的解決這個問題。

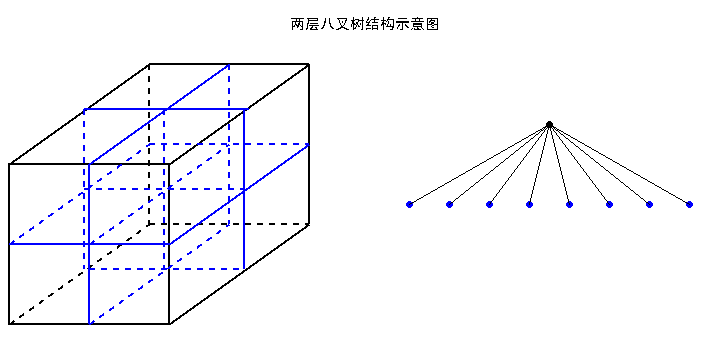
四叉樹（QuadTree）和八叉樹（Octree）

四叉樹或四元樹也被稱為Q樹（Q-Tree）。四叉樹廣泛應用於影象處理、空間資料索引、2D中的快速碰撞檢測、儲存稀疏資料等，而八叉樹（Octree）主要應用於3D圖形處理。八叉樹其實就是四叉樹在z軸上的延伸，原理差不多，四叉樹多用於地形管理，八叉樹多用於空間管理。

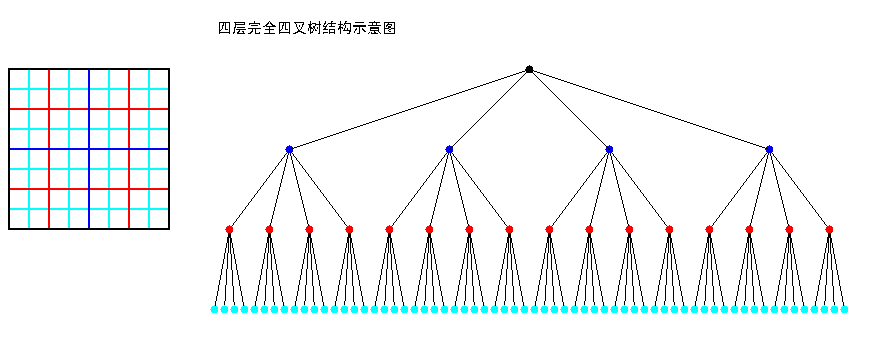
完全四叉樹

不完全四叉樹

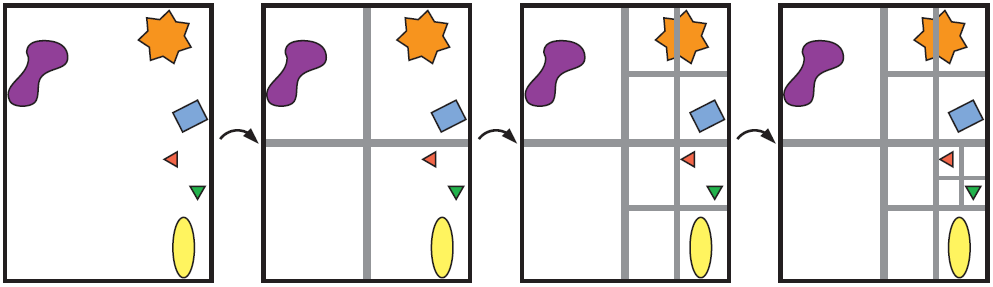
八叉樹類似軸對齊BSP樹。沿著軸對齊包圍盒的三條軸對其進行分割，分割點必須位於包圍盒的中心點，以這種方式生成8個新的包圍盒。八叉樹通過將整個場景包含在一個最小的軸對齊包圍盒中進行構造，遞迴分割，直到達到最大遞迴層次或包圍盒中包含的圖元小於某個閾值，其分割過程如圖4所示。八叉樹的使用方式與軸對齊BSP樹一樣，可以處理同類型的查詢，也可以用於遮擋裁剪演算法中。由於八叉樹是具有規則的結構，所以有些查詢會比BSP樹高效。

在八叉樹的結構中，通常將物體儲存在葉子節點中，其中有些物體必須儲存在多個葉子節點中。這種做法的一個最大弊端是增大資料量，而如果使用指標，則會導致八叉樹的編輯變得更加困難。“鬆散的八叉樹”演算法對這個問題進行了改進。

k-d樹（k-d tree）

K-D樹，即K-Dimensional Tree，是一種高維索引樹型資料結構。常用於大規模高維資料空間的最鄰近或者K鄰近查詢，例如影象檢索中高維影象特徵向量的K鄰近匹配，對KNN演算法的優化等。

K-D樹實際上是一棵高維二叉搜尋樹，與普通二叉搜尋樹不同的是，樹中儲存的是一些K維資料

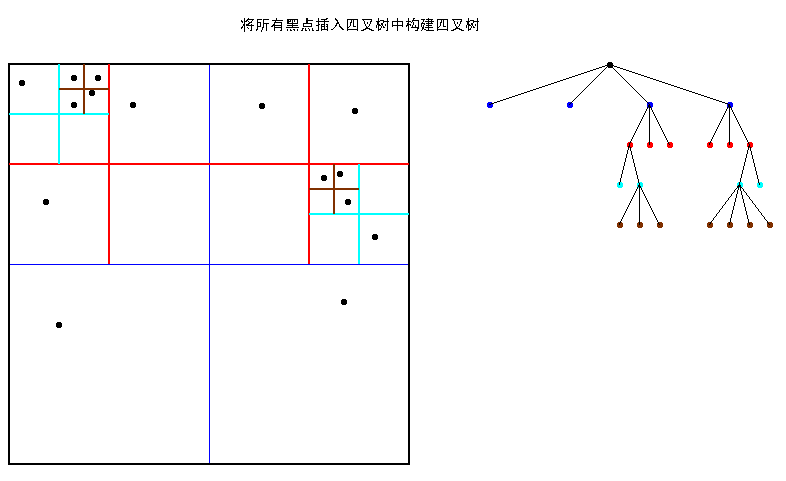
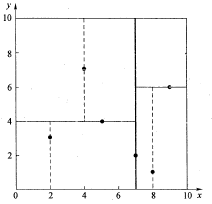
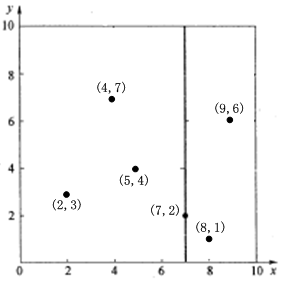
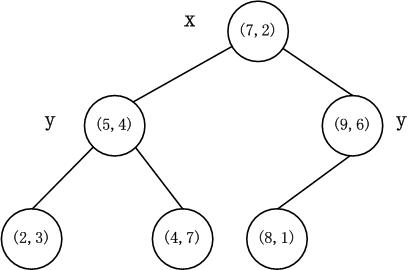
先以一個簡單直觀的例項來介紹k-d樹演算法。假設有6個二維資料點{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}，資料點位於二維空間內（如圖1中黑點所示）。k-d樹演算法就是要確定圖1中這些分割空間的分割線（多維空間即為分割平面，一般為超平面）。

k-d樹的構建是一個遞迴的過程。然後對左子空間和右子空間內的資料重複根節點的過程就可以得到下一級子節點（5,4）和（9,6）（也就是左右子空間的’根’節點），同時將空間和資料集進一步細分。如此反覆直到空間中只包含一個數據點。

每次劃分時，應該選擇哪個維度？最簡單的做法就是一個維度一個維度輪流著來，但是仔細想想，這種方法不能很好地解決問題。假設有這樣一種情況：我們需要切一個豆腐條，長度要遠遠大於寬度，要想把它切成儘量相同的小塊，顯然是先按照長度來切，這樣更合理，如果寬度比較窄，那麼這種效果更明顯。所以在K-D樹中，每次選取屬性跨度最大的那個來進行劃分，而衡量這個跨度的標準是什麼？ 無論是從數學上還是人的直觀感受方面來說，如果某個屬性的跨度越大，也就是說越分散，那麼這組資料的方差就越大，所以在K-D樹進行劃分時，可以每次選擇方差最大的屬性來劃分資料到左右子樹。

總結

場景管理是3D遊戲中很重要的環節，決定遊戲效能和效果。想當年2005年《完美國際》剛出的時候，驚歎於那超大世界無縫地圖，10年前的場景管理技術已經做的那麼出色！現在主流的遊戲引擎ue4，unity5，ce3等都自帶了很好的場景管理技術，不過作為底層引擎研發還是要了解這些技術的。

這些場景管理技術實際上也經常用到遮擋渲染、碰撞檢測、影象處理等多種領域當中。

目前為止，沒有一種空間結構絕對的最優，根據不同場合選擇不同的空間結構是一個明智的做法。八叉樹和BSP樹相比，由於其不需要儲存分割平面的資訊（因為每次都是在包圍盒的中心點進行分割），所以要比BSP效率更高。但是這不是絕對的，例如在一個細長的走廊場景中，用BSP明顯更合適，因為對沿著走廊的軸分割次數肯定要比另外兩個軸來得多，如果使用八叉樹，要麼浪費另外兩個軸的分割空間，要麼沿著走廊的軸分割不夠細。一般來說，對於室內場景使用BSP樹，因為
1）室內場景遮擋比較嚴重，使用BSP樹在特定的位置分割有助於提升效率；
2）室內很可能朝某個方向延伸比較多，比如一條細長的走廊。對於大規模室外場景，使用八叉樹比較好，因為場景中的物體比較分散，而且不會出現太多的遮擋，由於不用儲存分割平面位置，使用八叉樹這種規則的空間結構能夠提高效率。當然，如果這個大規模室外場景的物體主要集中在地面，使用四叉樹進行空間管理會比較好。