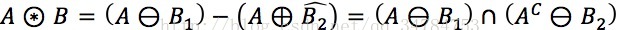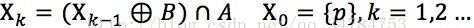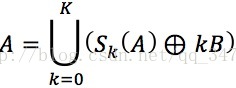【OpenCV影象處理】十九、數學形態學方法(中)
1.擊中擊不中運算
擊中擊不中(hit or miss)定義在交集為空集的兩個結構元素的膨脹和腐蝕運算的基礎上。設B =(B1,B2)表示結構元素對,且B1 ∩ B2 = ∅
則結構元素B對集合A的擊中積補種運算,記做
定義為:
→運算過程為:
(→當且僅當B1平移某一z值包含在集合A的內部,也就是B1擊中A且B2平移同一z值包含在集合A的外部(也就是B2擊不中A),這個條件同時成立時,B的原點位置的集合。
→由於擊中擊不中運算B1和B2兩個結構元素的交集為空集,也就是不會發生重合的現象,所以兩個結構元素B1,B2可以拼成為一個單一結構元素B來進行表示。
→結構元素B對集合A的擊中擊不中運算結果是B1對A腐蝕結果和B2對A補集的腐蝕結果的交集。
→
→擊中擊不中運算相當於一種條件比較嚴格的模板匹配
(→擊中擊不中運算的結構元素B也稱為擊中擊不中模板
→作用:
擊中擊不中運算對於研究二值影象中前景目標與背景之間的關係非常有效。
2.二值影象形態學的使用演算法
二值影象形態學主要應用是提取度表示和描述形狀有用的影象分量。
2.1 去噪
→二值化影象處理後經常會存在噪聲,例如,孤立的前景噪聲和目標區域中的小孔等等。
→如前所述,開運算和閉運算的結合處理是一種簡單的影象去噪方法。
設A為二值影象,B為結構元素,去噪過程一般為先進行開運算在進行閉運算,可以表示為
à = (AοB)·B
→Ã 為去噪後的影象,根據目標形狀和噪聲的尺寸,應選擇合適形狀和尺寸的結構元素。
需要注意的是:
如之前所述,開運算和閉運算結合的形態學處理後會影響目標原本的邊界和形狀,特別是當目標本身尺度比較小時,這種去噪處理的方法很容易破壞邊界的細節。
→對於複雜的邊界目標,一般不建議使用這種形態學方法對二值影象進行後處理。
2.2 邊界提取
結構元素B對集合A腐蝕的作用是收縮目標區域,集合A與腐蝕集合
邊界提取的基本原理是 腐蝕運算移除的邊界元素構成A的邊界集合
可以表示為:
→B(A)表示集合A的邊界集合,根據所需要的邊界連通性和寬度,應選擇合適尺寸和形狀的結構元素。
→使用3x3方形結構元素可以提取但畫素寬的4通道邊界
→使用3x3菱形結構可以提取但畫素寬的8聯通邊界
→使用5x5結構元素可以提取2~3個畫素寬的4的邊界
注意:
當結構元素B的原點位於或鄰近影象外邊界時,結構元素的一部分落在影象之外,常用的處理方法是假設影象邊界外部均為背景畫素,也就是0畫素。
→與其他的邊界跟蹤演算法相比,形態學邊界提取演算法簡單而且容易實現,並且可以進行“並行處理”。
2.3孔洞填充(種子填充)
→孔洞指的是由連通的外界包圍的背景區域。
→二值影象的孔洞填充的形態學演算法是以集合的膨脹,補集和交集的組合形式定義的。
設集合A表示邊界集合,B表示結構元素,給定邊界內的一個點P(種子),初始化集合X0中點P所在位置值為1,其他位置為0
孔洞填充的過程可以表示為:
當Xk=Xk-1時在第k步迭代終止,這時Xk為孔洞填充的最終結果,Xk與其邊界A的並集構成目標區域。
→若對膨脹不加以控制,則膨脹過程將會填充政府影象
→在每一次迭代過程中,與A補集進行交際將會膨脹集合限制在區域內部。這種在一定約束條件下的膨脹過程成為 條件膨脹
作用:
孔洞填充處理不會破壞目標原本的邊界和形狀,以此經常用於二值影象的後處理階段,以便進行後續的目標形狀,面積等影象分析工作。
2.4 連通分量提取
連通分量提取的形態學演算法是以集合的膨脹和交集的組合形式定義的
→設y是集合A中的連通分量,B表示結構元素,給定連通分量y中的一個點p,初始集合X0中點p所在位置為1,其餘的位置為0.
整個過程可以表示為:
當Xk=Xk-1時,迭代中值,y=Xk為連通分量提取的最終結果
→條件膨脹通過與集合A交集將膨脹劑和限制在連通分量的內部
→對於8連通分量的提取,→使用方形的結構元素進行條件膨脹
→對於4連通分量的提取,→使用菱形的結構元素進行條件膨脹
在二值影象後處理中通常需要移除小目標(噪聲分量)的干擾,除了使用結合開運算與閉運算方法外,也可以這樣進行操作:
→提取二值影象中所有連通分量,計算各個連通分量的畫素數,畫素數小於某一值域的連通分量中畫素賦值為0.
2.5 骨架
骨架是指在不改變目標拓撲結構的條件下,利用單畫素寬的細線表示目標,→目標的骨架和目標本身具有相同數量的連通分量和孔洞。
→目標的骨架保持了了目標的尤拉數(空洞區域內空洞數量的度量)
→形態學骨架指的是利用二值影象形態學的方法提取出目標的骨架
設A表示集合,B表示結構元素,一種形態學骨架計算由下式給出
→集合A的骨架S(A)由骨架子集Sk(A)構成
→骨架子集Sk(A)定義在腐蝕和開運算組合形式的基礎上,其計算公式為:
其中,AΘkB表示結構元素B對集合A的連續k次腐蝕,k為骨架子集的計算次數,數學表示式為
K=max{k | A Θ kB ≠ ∅}
→也就是說,k表示結構元素B將集合A腐蝕成為空集之前的最大次數,也就是一旦超過k次迭代,結構元素B將把集合A腐蝕成為空集。
注意:
骨架重構的過程是可逆的。→集合A可以利用骨架子集Sk(A)記性重構,計算公式為:
→式中,括號中的部分表示結構元素B對骨架子集Sk(A)的連續k次膨脹
注意:
這種演算法提取到的骨架並沒有達到最大限度的細化。
→由於在骨架提取的計算式中並沒有任何條件保證最終結果的連通性→這種演算法提取的骨架並不具有連通性
2.6 細化
細化是在保持目標連通性和邊界幾何特徵條件下,利用線狀結構來表示影象中的連通分量。細化的過程是不斷傷處目標區域的邊界畫素
→用將目標區域細化成為單畫素寬的線狀結構來表示。
→結構元素B對集合A的細化,記做
式中,等號左邊表示的是以此獨立的細化操作,定義一組結構元素B = {B1,B2,...,Bn},使用結構元素B中的所有元素連續作用於集合A
→Bi為Bi-1旋轉角度的形式
→整個過程以此使用結構元素B1,B2,...,Bn執行獨立的細化操作,後一次是在前一次結果上的繼續執行細化操作。
→根據上式完成一組結構元素成為一次迭代,反覆進行迭代,知道不再發生變化位置,這時,目標區域刪成為但畫素寬的細線。
2.7 粗化
→粗化是細化在形態學上是對偶過程,結構元素B對集合A的粗化,記做
計算式為:
上式表以此獨立的粗化操作過程
→定義一組結構元素B = {B1,B2,...,Bn},使用結構元素B中的所有元素連續作用於集合A
→Bi為Bi-1旋轉角度的形式,整個過程類似上面提到的細化過程,反覆進行迭代,直到不再發生變化為止 →粗化和細化具有相同形式的結構元素,不同的只是將所有的1值和0值進行互換。