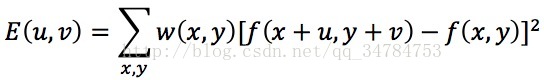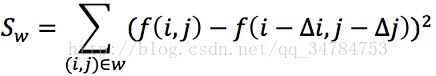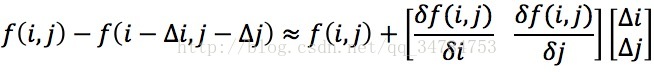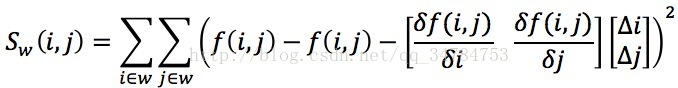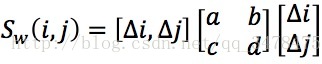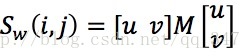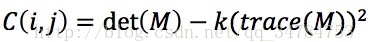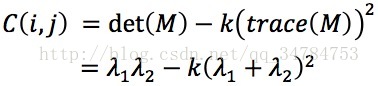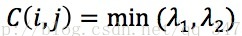【OpenCV影象處理】二十五、角點檢測
部落格參考 朱偉 等編著的《OpenCV影象處理程式設計例項》
======================================================================================
在很多應用場景中,影象畫素區域的興趣點區域對於目標檢測、目標跟蹤有著重要的意義。當興趣點周圍存在長方形區域時,最容易形成角點。
對於興趣點檢測,角點反映的是影象中區域性最大值或最小值的孤立點,可以理解為區域鄰域的小方塊,存在於不同方向的主邊緣處。視窗向任意方向的移動都會導致影象灰度的明顯變化,形成的點集稱為角點。
1. moravec角點
moravec角點是Moravec在1981年提出的角點檢測運算元,是最早的角點檢測演算法之一,常常應用於立體匹配。moravec角點的原理是通過滑動視窗畫素變化來實現角點檢測,首先計算視窗畫素的興趣值,也就是以當前畫素為中心畫素點,取一個正方形視窗ωxω(如ω=3),計算其0°,45°,90°和135°四個方向灰度差的平方和,取其中的最小值作為該興趣點的興趣值。
公式如下所示:
moravec角點檢測器對每一個興趣中心點進行滑窗遍歷,計算其相關8-鄰域方向的特徵關係,視窗的變化可以取3x3,5x5或7x7,畫素點位置變化可取
(u,v)={(-1,-1),(-1,0),(-1,-1),(0,-1),(0,1),(1,-1,),(1,0,),(1,-1)}。moravec角點檢測與其他型別角點檢測相比存在兩個缺點
(1).非均勻性響應。視窗特性決定了在進行角點檢測時,很容易受到鄰近特性的影響,一般在實驗操作前,先進行平滑操作。moravec角點檢測運算元對斜邊緣的響應很強,這是因為只考慮了45°的方向變化,而沒有在全部方向上考慮
(2).噪聲響應。由於視窗函式是一個二值函式,不管畫素離中心點的距離是多少,均賦予一樣的權重,致使其對應的噪聲也有很強的響應。moravec焦點檢測對噪聲十分敏感,一般在進行角點檢測前,先對影象興趣區域採用較大的視窗或先進行平滑操作。
moravec角點檢測具體程式如下所示:
//moravec角點檢測 #include <iostream> #include <opencv2\core\core.hpp> #include <opencv2\highgui\highgui.hpp> #include <opencv2\imgproc\imgproc.hpp> using namespace cv; using namespace std; //moravec角點檢測函式 Mat MoravecCorners(Mat srcImage, int kSize, int threshlod); int main() { Mat srcImage = imread("2345.jpg", 0); if (!srcImage.data) { cout << "讀入圖片錯誤!" << endl; system("pause"); return -1; } Mat resMorMat = MoravecCorners(srcImage, 5, 10000); imshow("原影象", srcImage); imshow("標記角點影象", resMorMat); waitKey(); return 0; } Mat MoravecCorners(Mat srcImage, int kSize, int threshlod) { Mat resMorMat = srcImage.clone(); //獲取初始化引數資訊 int r = kSize / 2; const int rowsNum = srcImage.rows; const int colsNum = srcImage.cols; int nCount = 0; CvPoint *pPoint = new CvPoint[rowsNum*colsNum]; //影象遍歷 for (int i = r; i < srcImage.rows - r; i++) { for (int j = r; j < srcImage.cols - r; j++) { int wV1, wV2, wV3, wV4; wV1 = wV2 = wV3 = wV4 = 0; //計算水平方向窗內的興趣值 for (int k = -r; k < r; k++) { wV1 += (srcImage.at<uchar>(i, j + k) - srcImage.at<uchar>(i, j + k + 1))*(srcImage.at<uchar> (i, j + k) - srcImage.at<uchar>(i, j + k + 1)); } //計算垂直方向窗內的興趣值 for (int k = -r; k < r; k++) { wV2 += (srcImage.at<uchar>(i + k, j) - srcImage.at<uchar>(i + k + 1, j))*(srcImage.at<uchar> (i + k, j) - srcImage.at<uchar>(i + k + 1, j)); } //計算45°方向窗內的興趣值 for (int k = -r; k < r; k++) { wV3 += (srcImage.at<uchar>(i + k, j + k) - srcImage.at<uchar>(i + k + 1, j))*(srcImage.at<uchar> (i + k, j + k) - srcImage.at<uchar>(i + k + 1, j + k + 1)); } //計算135°方向窗內的興趣值 for (int k = -r; k < r; k++) { wV4 += (srcImage.at<uchar>(i + k, j - k) - srcImage.at<uchar>(i + k + 1, j - k - 1))*(srcImage.at<uchar> (i + k, j - k) - srcImage.at<uchar>(i + k + 1, j - k - 1)); } //取其中的最小值作為這個畫素點的最終興趣值 int value = min(min(wV1, wV2), min(wV3, wV4)); //若興趣值大於閾值,則將點的座標存入陣列中 if (value>threshlod) { pPoint[nCount] = cvPoint(j, 1); nCount++; } } } //繪製興趣點 for (int i = 0; i < nCount; i++) { circle(resMorMat, pPoint[i], 5, Scalar(255, 0, 0)); } return resMorMat; }
2.harris角點
harris角點在moravec角點的基礎上進行了改進,對於比moravec角點的連續平方求和,它引入了局部變化因子,利用高斯權重函式特性進行角點檢測。
對於影象f(x,y),任取視窗塊W,進行評議Δx、Δy,考慮道具部特性變化,計算影象平移後窗口變化值之差的平方和如下:
考慮到響應特性,角點不會受到光圈引數的影響,對於Sw(Δi,Δj)中的高斯響應部分,利用泰勒展開,對於平移後的影象,可變換成下式:
將上式中f(i,j) - f(i-Δi,j-Δj)的近似值代入到Sw(i,j)中可以得到:
最後進行矩陣變換,可以得到:
其中a = fx·fx,b = c =fx·fy,d = fy·fy,對於區域性微小移動量[u,v],視窗移動導致的影象灰度變化,實際可理解為矩陣變換中實對稱矩陣M滿足:
其中M為2x2矩陣,由影象導數可以得到引數對應於a,b,c,d。對於區域性結構矩陣M代表的鄰域,將實對稱矩陣對角化處理後,對應項可以理解為旋轉因子,經過對角化處理以後,根據兩個正交方向的變化分量計算其相應的特徵值λ1和λ2。如果兩個熱正值均較大而且數值相當,則影象視窗在所有方向上的移動都將產生明顯的灰度變化,可判斷其將形成角點。如果僅有一個特徵值較高且遠大於另一個特徵值,則得到相應的邊緣,其他情況可以得到穩定的區域。基於上述特徵值特性,harris角點理論提出了相應的角點響應函式,如下所示:
其中k為常量因子,通常情況下取值為0.04~0.06,對影象視窗內資料進行求和加權,實際上可以更好的刻畫視窗中心特性。harris角點在實踐複雜度上更高於moravec角點,對噪聲也十分敏感,也存在非均勻響應。儘管如此,harris角點檢測器還是目前應用最廣泛的檢點檢測器之一,它的檢測率高,而且可以得到重複相應。
harris角點檢測演算法的實現步驟如下所示:
(1).利用水平與數值差分運算元對影象進行卷積操作,計算得到相應的fx,fy,根據實對稱矩陣M的組成,計算對應矩陣元素的值。
(2).利用高斯函式對矩陣M進行平滑操作,得到新的M矩陣,步驟1和2可以改變書序,也可以先對影象進行高斯濾波,再求相應方向上的梯度大小。
(3).對每一畫素和給定的鄰域視窗,計算區域性特徵結果矩陣M的特徵值和相應函式C(i,j) = det(M) -k(trace(M))^2
(4).選取相應函式C的閾值,根據非極大值抑制原理,同事滿足閾值及某鄰域內的區域性極大值為候選角點。
harris角點檢測的具體程式碼如下所示:
#include <iostream>
#include <stdlib.h>
#include <opencv2\core\core.hpp>
#include <opencv2\highgui\highgui.hpp>
#include <opencv2\imgproc\imgproc.hpp>
using namespace cv;
using namespace std;
//計算Harris角點的函式
void CornerHarris(const Mat& srcImage, Mat &result,
int blocksize, int kSize, double k);
int main()
{
Mat srcImage = imread("2345.jpg");
if (!srcImage.data)
{
cout << "讀入圖片錯誤!" << endl;
system("pause");
return -1;
}
imshow("srcImage", srcImage);
Mat grayImage, result;
cvtColor(srcImage, grayImage, CV_BGR2GRAY);
result = Mat::zeros(srcImage.size(), CV_32FC1);
//角點檢測引數
int blocksize = 2;
int aperatureSize = 3;
double k = 0.04;
//進行角點檢測
CornerHarris(grayImage, result, blocksize, aperatureSize, k);
//矩陣進行歸一化
normalize(result, result, 0, 255, NORM_MINMAX,CV_32FC1,Mat());
convertScaleAbs(result, result);
//繪製角點檢測結果
for (int j = 0; j < result.rows; j++)
{
for (int i = 0; i < result.cols; i++)
{
if ((int)result.at<uchar>(j,i)>150)
{
circle(srcImage, Point(j,i), 5, Scalar(0), 2, 8, 0);
}
}
}
imshow("結果圖", result);
waitKey();
return 0;
}
void CornerHarris(const Mat& srcImage, Mat &result, int blocksize, int kSize, double k)
{
Mat src;
srcImage.copyTo(src);
result.create(srcImage.size(), CV_32F);
int depth = src.depth();
//檢測掩膜尺寸
double scale = (double)(1 << ((kSize > 0 ? kSize : 3) - 1))*blocksize;
if (depth == CV_8U)
scale *= 255;
scale = 1. / scale;
//進行Sobel濾波
Mat dx, dy;
Sobel(src, dx, CV_32F, 1, 0, kSize, scale, 0);
Sobel(src, dy, CV_32F, 0, 1, kSize, scale, 0);
Size size = src.size();
Mat cov(size, CV_32FC3);
int i, j;
//求解水平與數值梯度
for (int i = 0; i < size.height; i++)
{
float *covData = (float*)(cov.data + i*cov.step);
const float *dxData = (const float*)(dx.data + i*dx.step);
const float *dyData = (const float*)(dy.data + i*dy.step);
for (int j = 0; j < size.width; j++)
{
float dx_ = dxData[j];
float dy_ = dyData[j];
covData[3 * j] = dx_*dx_;
covData[3 * j + 1] = dy_*dy_;
covData[3 * j + 2] = dx_*dy_;
}
}
//對影象進行boxfilter操作
boxFilter(cov, cov, cov.depth(), Size(blocksize, blocksize),
Point(-1, -1), false); //最後一個引數false表示 濾波不進行歸一化
//判斷影象的連續性
if (cov.isContinuous() && result.isContinuous())
{
size.width *= size.height;
size.height = 1;
}
else
size = result.size();
//計算響應函式
for (i = 0; i < size.height; i++)
{
//獲取影象的矩陣指標
float *resultData = (float*)(result.data + i*result.step);
const float *covData = (const float*)(cov.data + i*cov.step);
for (j = 0; j < size.width; j++)
{
//角點響應生成
float a = covData[3 * j];
float b = covData[3 * j + 1];
float c = covData[3 * j + 2];
resultData[j] = a*c - b*b - k*(a + c)*(a + c);
}
}
}3.Shi-Tomasi角點
在1994年發表的論文“Good Features to Track”一文中基於harris原理提出了改進演算法,採用和harris不同的角點響應函式,已知
harris角點響應函式定義為:
其中λ1和λ2分別為M矩陣的兩個特徵值,Shi-Tomasi角點檢測則選取了不同的角點響應函式:
Shi-Tomasi角點檢測劃分相關一對一配對,依據影象的角點特徵、影象灰度和位置資訊,採用最大互相關函式進行相似度計算,最終實現角點檢測。
在OpenCV中利用函式goodFeaturesToTrack()函式實現該角點的檢測演算法,下面首先簡單介紹一下這個函式
函式原型為:
void goodFeaturesToTrack( InputArray image, OutputArray corners, int maxCorners, double qualityLevel, double minDistance,
InputArray mask=noArray(), int blockSize=3,bool useHarrisDetector=false, double k=0.04 );第二個引數corners為檢測到的角點輸出矩陣
第三個引數maxCorners表示檢測到的角點輸出的最大數目
第四個引數qualityLevel表示可允許接受的角點最差質量,這個引數使用時將該數值乘以最佳角點的質量數值來刪除角點
第五個引數minDistance表示返回角點間的最小的歐式距離,用於限定近鄰畫素被檢測出角點的可能性
第六個引數mask表示可選引數為興趣區域,若輸入影象非空,它將被限定到檢測到角點區域
第七個引數blockSize表示畫素鄰域中計算協方差矩陣的視窗的尺寸
第八個引數useHarrisDetector表示應用harris檢測演算法來確定,有預設引數false
第九個引數k表示一個經驗引數,有預設值0.04
應用這個函式進行Shi-Tomasi角點檢測的程式如下所示:
//實現Shi-Tomasi角點檢測
#include <stdlib.h>
#include <iostream>
#include <opencv2\core\core.hpp>
#include <opencv2\highgui\highgui.hpp>
#include <opencv2\imgproc\imgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("2345.jpg");
if (!srcImage.data)
{
cout << "讀入圖片有誤!" << endl;
system("pause");
return -1;
}
Mat srcGray;
cvtColor(srcImage, srcGray, CV_BGR2GRAY);
//設定角點檢測引數
vector<Point2f>vecCorners;
//可允許接受的角點最差質量
double qualityLevel = 0.01;
//角點間最小的歐氏距離
double minDistance = 10;
//畫素鄰域中計算協方差矩陣視窗的尺寸
int blockSize = 3;
bool useHarrisDetector = false;
double k = 0.04;
//檢測到的角點輸出的最大數目
int maxCorners = 50;
int maxTrackbar = 100;
Mat result = srcImage.clone();
//呼叫函式進行Shi-Tomasi角點檢測
goodFeaturesToTrack(srcGray, vecCorners, maxCorners, qualityLevel,
minDistance, Mat(), blockSize, useHarrisDetector, k);
cout << "Corners:" << vecCorners.size() << endl;
//繪製檢測角點
for (size_t i = 0; i < vecCorners.size(); i++)
{
circle(result, vecCorners[i], 4, Scalar(0, 0, 255), 2);
}
imshow("原影象", srcImage);
imshow("結果影象", result);
waitKey();
return 0;
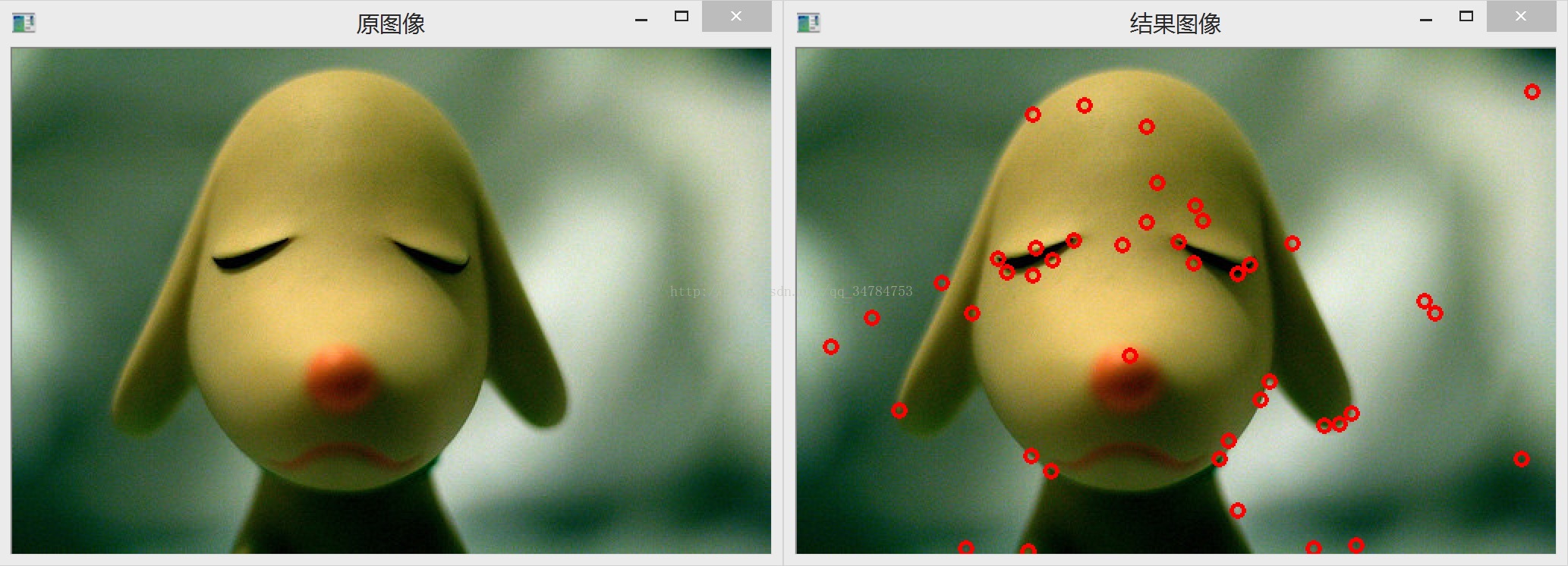
}執行後結果如下所示: