matlab影象融合
matlab影象融合
[r,c]=size(y1); %根據低頻融合演算法進行影象融合
for i=1:r %首先取兩幅源影象相應的小波分解係數絕對值最大者的值作為融合影象的分解係數
for j=1:c
if( abs(y1(i,j)) >= abs(y2(i,j)) )
y3(i,j)=y1(i,j);
elseif( abs(y1(i,j)) < abs(y2(i,j)) )
y3(i,j)=y2(i,j);
end
% y3(i,j)=max(abs(y1(i,j)) , abs(y2(i,j)) ); % 這行程式碼是錯誤的,取了絕對值而非實際值
end
end
(2)低頻融合的物件
低頻融合的物件是N級分解後圖像的LL-N子影象,相應的程式程式碼為:
LLa=y1(1:r/(2^dim),1:c/(2^dim)); %呼叫lowfrefus函式對低頻部分的小波分解係數進行融合
LLb=y2(1:r/(2^dim),1:c/(2^dim));
y3(1:r/(2^dim),1:c/(2^dim))=lowfrefus(LLa,LLb);
(3)低頻融合策略的程式程式碼
這一部分程式程式碼的實現難度不大,根據演算法原理中列出的公式可以很快寫出相應的程式碼。不過有些細節問題還是要花心思處理,比如區域大小的確定、區域邊界與影象邊界的關係、區域中心與區域中各點的權值確定、區域中心在原始影象中的具體位置等等。
function y = lowfrefus(A,B);
% 函式 Y=LOWFREFUS(A,B) 對輸入的兩個小波分解係數矩陣,根據低頻融合演算法,得出融合影象的低頻小波分解係數
[row,col]=size(A); %求出分解係數矩陣的行列數
alpha=0.5; %alpha是方差匹配度比較的閾值
for i=1:row %根據低頻融合演算法,先求出矩陣A,B中以點P為中心的區域方差和方差匹配度
forj=1:col % 再根據方差匹配度與閾值的比較確定融合影象的小波分解係數
[m2p(i,j),Ga(i,j),Gb(i,j)]= area_var_match(A,B,[i,j]);
Wmin=0.5-0.5*((1-m2p(i,j))/(1-alpha));
Wmax=1-Wmin;
ifm2p(i,j)<alpha % m2p表示方差匹配度
ifGa(i,j)>=Gb(i,j) % 若匹配度小於閾值,則取區域方差大的相應點的分解係數作為融合影象的分解係數
y(i,j)=A(i,j);
else
y(i,j)=B(i,j);
end
else %若匹配度大於閾值,則採取加權平均方法得出相應的分解係數
ifGa(i,j)>=Gb(i,j)
y(i,j)=Wmax*A(i,j)+Wmin*B(i,j);
else
y(i,j)=Wmin*A(i,j)+Wmax*B(i,j);
end
end
end
end
function w = weivec(x,p);
% 函式 W=WEIVEC(X,P) 對輸入的r*c矩陣,計算出以點p為中心時矩陣各點的對應權值
% 距離點p越近,權值就越大。權值是通過行和列的高斯分佈加權相加得到的。
[r,c]=size(x);
p1=p(1); p2=p(2);
sig=1;
for i=1:r
for j=1:c
w(i,j)=0.5*(gaussmf(i,[sigp1])+gaussmf(j,[sig p2]));
end
end
function [m2p,Ga,Gb] =area_var_match(A,B,p);
% 函式 area_var_match 計算兩個輸入矩陣以點p為中心的區域方差以及區域方差匹配度
level=1; % 設定區域的大小
[subA,mpa,npa]=submat(A,p,level); %submat 函式取輸入矩陣中以點P為中心、階數為(2*level+1)的方陣作為子矩陣
[subB,mpb,npb]=submat(B,p,level);
[r,c]=size(subA);
w=weivec(subA,[mpa npa]); %獲取子矩陣的權值分佈
averA=sum(sum(subA))/(r*c); % 計運算元矩陣的平均值
averB=sum(sum(subB))/(r*c);
Ga=sum(sum(w.*(subA-averA).^2)); %計運算元矩陣的區域方差
Gb=sum(sum(w.*(subB-averB).^2));
if(Ga==0)&(Gb==0) % 計算兩個子矩陣的區域方差匹配度
m2p=0;
else
m2p=2*sum(sum(w.*abs(subA-averA).*abs(subB-averB)))/(Ga+Gb);
end
function [smat,mp,np] = submat(x,p,level);
% 函式 submat 取輸入矩陣中以點P為中心、階數為(2*level+1)的方陣作為輸出的子矩陣
[row,col]=size(x);
m=p(1); n=p(2);
if (m>row)||(n>col)
error('Point p isout of matrix X !');
return;
end
if((2*level+1)>row)||((2*level+1)>col)
error('Too largesample area level !');
return;
end
% 設定子矩陣的邊界值
up=m-level; down=m+level;
left=n-level; right=n+level;
% 若子矩陣的某一邊界值超出輸入矩陣的相應邊界,就進行邊界處理,
% 即超出邊界後往相反方向平移,使其恰好與邊界重合
if left<1
right=right+1-left;
left=1;
end
if right>col
left=left+col-right;
right=col;
end
if up<1
down=down+1-up;
up=1;
end
if down>row
up=up+row-down;
down=row;
end
% 獲取作為輸出的子矩陣,並計算點p在輸出的子矩陣中的位置
smat = x(up:down,left:right);
mp=m-up+1;np=n-left+1;
下面我們給出相應的圖片示例,圖1 是一幅遠景清晰近景模糊的圖片,圖2 是一幅遠景模糊近景清晰的圖片,圖3是融合效果圖。



影象融合是將兩幅或多幅影象融合在一起,以獲取對同一場景的更為精確、更為全面、更為可靠的影象描述。融合演算法應該充分利用各原影象的互補資訊,使融合後的影象更適合人的視覺感受,適合進一步分析的需要;並且應該統一編碼,壓縮資料量,以便於傳輸。
影象融合可分為三個層次:
1. 畫素級融合
2. 特徵級融合
3. 決策級融合
其中畫素級融合是最低層次的融合,也是後兩級的基礎。它是將各原影象中對應的畫素進行融合處理,保留了儘可能多的影象資訊,精度比較高, 因而倍受人們的重視。畫素級的影象融合方法大致可分為三大類:
1. 簡單的影象融合方法
2. 基於塔形分解(如Laplace塔形分解、比率塔等)的影象融合方法
3. 基於小波變換的影象融合方法
小波變換是影象的多尺度、多解析度分解,它可以聚焦到影象的任意細節,被稱為數學上的顯微鏡。近年來,隨著小波理論及其應用的發展,已將小波多解析度分解用於畫素級影象融合。小波變換的固有特性使其在影象處理中有如下優點:
1. 完善的重構能力,保證訊號在分解過程中沒有資訊損失和冗餘資訊;
2. 把影象分解成平均影象和細節影象的組合,分別代表了影象的不同結構,因此容易提取原始影象的結構資訊和細節資訊;
3. 具有快速演算法,它在小波變換中的作用相當於FFT演算法在傅立葉變換中的作用,為小波變換應用提供了必要的手段;
4. 二維小波分析提供了與人類視覺系統方向相吻合的選擇性影象。
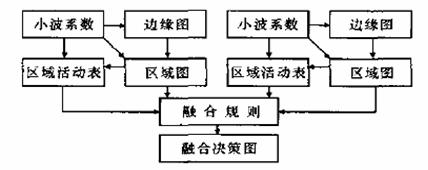
——畫素級影象融合的主要步驟
以兩幅影象的融合為例。設A,B為兩幅原始影象,F為融合後的影象。若對二維影象進行N層的小波分解,最終將有(3N+1)個不同頻帶,其中包含3N 個高頻子影象和1個低頻子影象。其融合處理的基本步驟如下:
(1)對每一原影象分別進行小波變換,建立影象的小波塔型分解;
(2)對各分解層分別進行融合處理。各分解層上的不同頻率分量可採用不同的融合運算元進行融合處理,最終得到融合後的小波金字塔;
(3)對融合後所得小波金字塔進行小波重構,所得到的重構影象即為融合影象。
圖 1
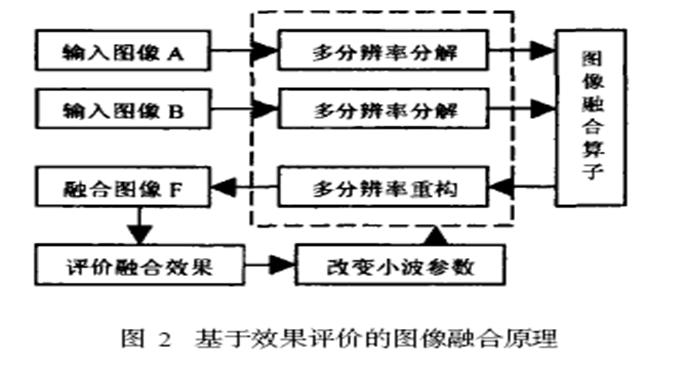
在影象融合過程中,小波基的種類和小波分解的層數對融合效果有很大的影響,對特定的影象來說,哪一種小波基的融合效果最好,分解到哪一層最合適,都是需要考慮的問題。為此可以通過引入融合效果的評價來構成一個閉環系統。如圖2所示。