1、小波變換的理解

傅立葉變換——短時傅立葉變換——小波變換。

參考文獻：以下兩篇參考資料講述得十分清楚，有助於理解小波變換。

但具體的數學角度闡述，請參考其他資料。

（1）知乎專欄：形象易懂講解演算法I——小波變換

https://zhuanlan.zhihu.com/p/22450818

（2）知乎專欄：傅立葉分析之掐死教程。

https://zhuanlan.zhihu.com/p/19763358

2、小波包分解

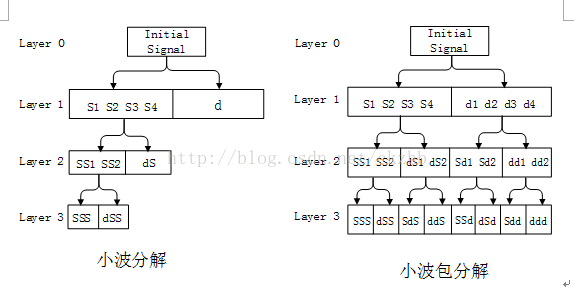
小波包是為了克服小波分解在高頻段的頻率解析度較差，而在低頻段的時間解析度較差的問題的基礎上而提出的。

它是一種更精細的訊號分析的方法，提高了訊號的時域解析度。

下面是兩者的對比圖：

3、能量譜

      基於小波包分解提取多尺度空間能量特徵的原理是把不同分解尺度上的訊號能量求解出來，將這些能量值按尺度順序排列成特徵向量供識別使用。

20180510補充更新：具體計算公式如下所示，本文中未使用重構後的係數進行能量值計算，直接使用小波包分解後的係數，參考文獻《基於小波包能量特徵的滾動軸承故障監測方法 》。

4、Matlab程式碼

給出兩部分程式碼，寫成兩個函式。一個是小波包分解與重構，另一個是能量譜函式。

下載地址：https://download.csdn.net/download/ckzhb/10030651

程式碼名稱：wavelet_packetdecomposition_reconstruct

function wpt= wavelet_packetdecomposition_reconstruct( x,n,wpname )
%% 對訊號進行小波包分解，得到節點的小波包係數。然後對每個節點係數進行重構。 
% Decompose x at depth n with wpname wavelet packets.using Shannon entropy.
%   
%  x
 
-input signal,列向量。
%  n-the number of decomposition layers
%  wpname-a particular wavelet.type:string.
%
%Author hubery_zhang
%Date 20170714

%%
wpt=wpdec(x,n,wpname);
% Plot wavelet packet tree (binary tree)
plot(wpt)
%% wavelet packet coefficients.default：use the front 4.
cfs0=wpcoef(wpt,[n 0]);
cfs1=wpcoef(wpt,[n 1]);
cfs2=wpcoef(wpt,[n 2]);
cfs3=wpcoef(wpt,[n 3]);
figure;
subplot(5,1,1);
plot(x);
title(‘原始訊號’);
subplot(5,1,2);
plot(cfs0);
title([‘結點 ‘,num2str(n) ’ 1’,’ 係數’])
subplot(5,1,3);
plot(cfs1);
title([‘結點 ‘,num2str(n) ’ 2’,’ 係數’])
subplot(5,1,4);
plot(cfs2);
title([‘結點 ‘,num2str(n) ’ 3’,’ 係數’])
subplot(5,1,5);
plot(cfs3);
title([‘結點 ‘,num2str(n) ’ 4’,’ 係數’])
%% reconstruct wavelet packet coefficients.
rex0=wprcoef(wpt,[n 0]);
rex1=wprcoef(wpt,[n 1]);
rex2=wprcoef(wpt,[n 2]);
rex3=wprcoef(wpt,[n 3]);
figure;
subplot(5,1,1);
plot(x);
title(‘原始訊號’);
subplot(5,1,2);
plot(rex0);
title([‘重構結點 ‘,num2str(n) ’ 1’,’ 係數’])
subplot(5,1,3);
plot(rex1);
title([‘重構結點 ‘,num2str(n) ’ 2’,’ 係數’])
subplot(5,1,4);
plot(rex2);
title([‘重構結點 ‘,num2str(n) ’ 3’,’ 係數’])
subplot(5,1,5);
plot(rex3);
title([‘重構結點 ‘,num2str(n) ’ 4’,’ 係數’])
end

程式碼名稱：wavelet_energy_spectrum

function E = wavelet_energy_spectrum( wpt,n )

%% 計算每一層每一個節點的能量

%  wpt-wavelet packet tree

%  n-第n層能量

%

% Author hubery_zhang

% Date  20170714

%%
% 求第n層第i個節點的係數
E(1:2^n )=0;
for i=1:2^n
E(i) = norm(wpcoef(wpt,[n,i-1]),2)^2; %20180604更新 原始碼：E(i) = norm(wpcoef(wpt,[n,i-1]),2)
end
%求每個節點的概率
E_total=sum(E);
for i=1:2^n
p_node(i)= 100*E(i)/E_total;
end
% E = wenergy(wpt); only get the last layer
figure;
x=1:2^n;
bar(x,p_node);
title([‘第’,num2str(n),‘層’]);
axis([0 2^n 0 100]);
xlabel(‘結點’);
ylabel(‘能量百分比/%’);
for j=1:2^n
text(x(j),p_node(i),num2str(p_node(j),’%0.2f’),…
‘HorizontalAlignment’,‘center’,…
‘VerticalAlignment’,‘bottom’)
end

end

1、小波變換的理解

傅立葉變換——短時傅立葉變換——小波變換。

參考文獻：以下兩篇參考資料講述得十分清楚，有助於理解小波變換。

但具體的數學角度闡述，請參考其他資料。

（1）知乎專欄：形象易懂講解演算法I——小波變換

https://zhuanlan.zhihu.com/p/22450818

（2）知乎專欄：傅立葉分析之掐死教程。

https://zhuanlan.zhihu.com/p/19763358

2、小波包分解

小波包是為了克服小波分解在高頻段的頻率解析度較差，而在低頻段的時間解析度較差的問題的基礎上而提出的。

它是一種更精細的訊號分析的方法，提高了訊號的時域解析度。

下面是兩者的對比圖：

3、能量譜

      基於小波包分解提取多尺度空間能量特徵的原理是把不同分解尺度上的訊號能量求解出來，將這些能量值按尺度順序排列成特徵向量供識別使用。

20180510補充更新：具體計算公式如下所示，本文中未使用重構後的係數進行能量值計算，直接使用小波包分解後的係數，參考文獻《基於小波包能量特徵的滾動軸承故障監測方法 》。

4、Matlab程式碼

給出兩部分程式碼，寫成兩個函式。一個是小波包分解與重構，另一個是能量譜函式。

下載地址：https://download.csdn.net/download/ckzhb/10030651

程式碼名稱：wavelet_packetdecomposition_reconstruct

function wpt= wavelet_packetdecomposition_reconstruct( x,n,wpname )
%% 對訊號進行小波包分解，得到節點的小波包係數。然後對每個節點係數進行重構。 
% Decompose x at depth n with wpname wavelet packets.using Shannon entropy.
%   
%  x-input signal,列向量。
%  n-the number of decomposition layers
%  wpname-a particular wavelet.type:string.
%
%Author hubery_zhang
%Date 20170714