漢諾塔問題不管在任何程式語言裡都是經典問題，是採用遞迴演算法的經典案例，該問題可以抽象如下：

一    3根圓柱A，B，C，其中A上面串了n個圓盤

二    這些圓盤從上到下是按從小到大順序排列的，大的圓盤任何時刻不得位於小的圓盤上面

三    每次移動一個圓盤，最終實現將所有圓盤移動到Ｃ上

    利用Python語言接近自然語言的特性，開發者可以更容易的將遞迴演算法翻譯成程式語句，需要的程式碼量很小。漢諾塔問題的解決步驟用語言描述很簡單，僅三步：

A，B，C三個圓柱，分別為初始位，過渡位，目標位，設A柱為初始位，C位為最終目標位

（1）將最上面的n-1個圓盤從初始位移動到過渡位

（2）將初始位的最底下的一個圓盤移動到目標位

（3）將過渡位的n-1個圓盤移動到目標位

對於遞迴演算法中的巢狀函式f（n-1）來說，其初始位，過渡位，目標位發生了變化

具體程式碼如下：

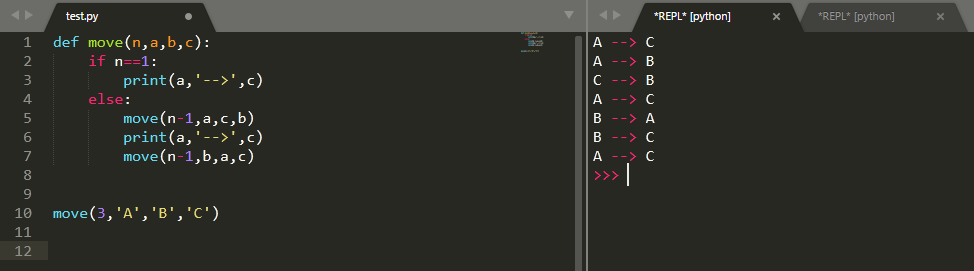
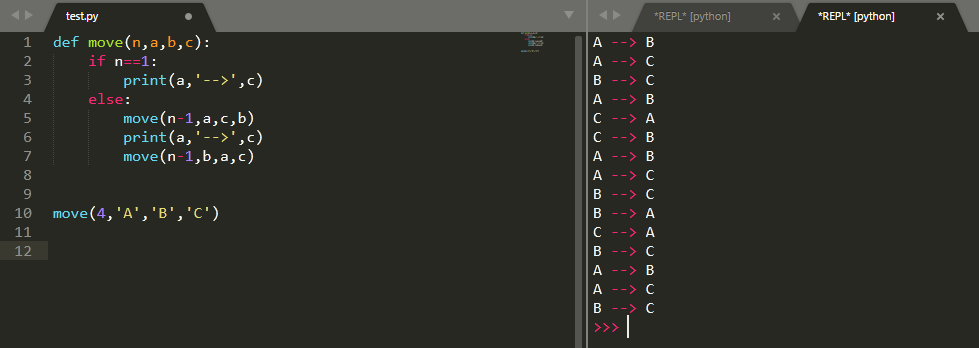
def move(n,a,b,c):   #n為圓盤數，a代表初始位圓柱，b代表過渡位圓柱，c代表目標位圓柱
	if n==1:
		print(a,'-->',c)
	else:
		move(n-1,a,c,b)   #將初始位的n-1個圓盤移動到過渡位，此時初始位為a，上一級函式的過渡位b即為本級的目標位，上級的目標位c為本級的過渡位
		print(a,'-->',c)

		move(n-1,b,a,c)   #將過渡位的n-1個圓盤移動到目標位，此時初始位為b，上一級函式的目標位c即為本級的目標位，上級的初始位a為本級的過渡位
 

程式執行結果如下：