PCA 演算法也叫主成分分析（principal components analysis），主要是用於資料降維的。關於降維，可以這樣理解，一組資料有n個feature（客戶年齡，收入，每個月消費額度等等），每一個feature有一系列的觀測點。而這n個feature中有一些存線上性相關，比如對於某些群體而言，收入和消費是線性相關的。此時我們進行多維度資料分析時只需要考慮其中一個引數就可以足夠了，這樣就能減少一個feature（維度），PCA方法就是用嚴謹的資料方法實現了這一過程。具體原理見下文，寫十分清楚：

http://blog.codinglabs.org/articles/pca-tutorial.html

本例子主要介紹了sklearn中PCA的簡單實現以及在降維後的快速聚類：

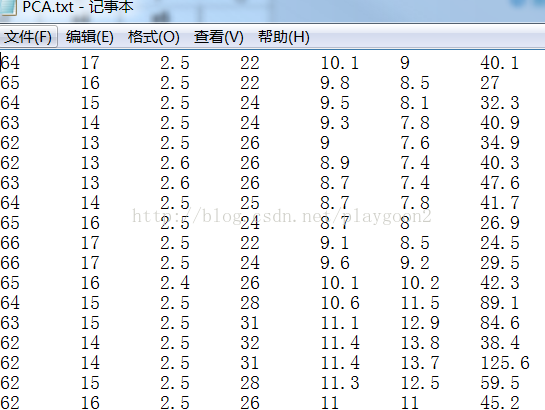
以下為輸入資料

from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import pandas as pd
import numpy as np
#pca.txt是一個沒有表頭的多維資料，一共有7列，利用pandas讀取
df = pd.read_table('d:/PCA.txt')
#將df轉換成矩陣
dataMat = np.array(df)
#呼叫sklearn中的PCA，其中主成分有5列
pca_sk = PCA(n_components=5)
#利用PCA進行降維，資料存在newMat中
newMat = pca_sk.fit_transform(dataMat)
#利用KMeans進行聚類，分為3類
kmeans = KMeans(n_clusters=3,random_state=0).fit(newMat)
#labels為分類的標籤
labels = kmeans.labels_
#把標籤加入到矩陣中用DataFrame生成新的df，index為類別的編號，這裡是0,1,2
dataDf = pd.DataFrame(newMat,index=labels,columns=['x1','x2','x3','x4','x5'])
#資料儲存在excel檔案中
dataDf.to_excel('d:/pca_cluster.xls')
print(pca_sk.explained_variance_ratio_)
 

[ 0.85847673  0.09840701  0.0223092   0.01740787  0.00304186]

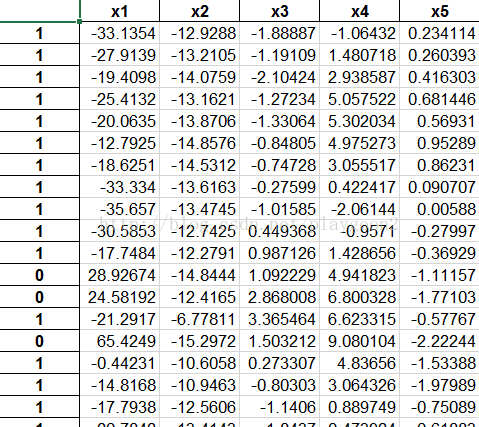
結果為每一列所佔特徵方差的百分比，總和為0.9996說明降維保持了原資料的特徵

excel資料輸出結果為