reference: 

http://blog.csdn.net/warmyellow/article/details/5454943

首先說一下協方差矩陣， 之前大家肯定都學過，忘了的可以稍微看一眼：

LDA是多個類的之前的判別，一個類之間的資料我們可以用方差或者標準差，但是多個類之間顯然不能再用var or std-var,  這時候就要用到cov.

協方差： cov(X, Y) = i(1...n) (Xi - X_mean)(Yi - Y_mean) / (n-1)

if cov(X, Y) > 0:  X 與 Y 正相關； 

if cov(X, Y) < 0:  X 與 Y 負相關；

if cov(X, Y) ＝ 0:  X 與 Y 不相關， 即相互獨立；

現在我們看一個三維的協方差矩陣，表示兩兩類之間的關係， 看一下應該就能明白了：

協方差矩陣C = [[cov(x, x), cov(y, x), cov(z, x)], [cov(x , y), cov(y, y), cov(z,y)}, [cov(x, z), cov(y, z), cov(z, z)]]

可以看出協方差矩陣是一個對角矩陣， 而對角線則是各個維度的方差。 

NOTE:  注意是各個維度之間的關係，在具體給出的矩陣中，看每一行是一個維度的所有樣本還是每個維度的一個樣本，再確定是按列取還是按行取。

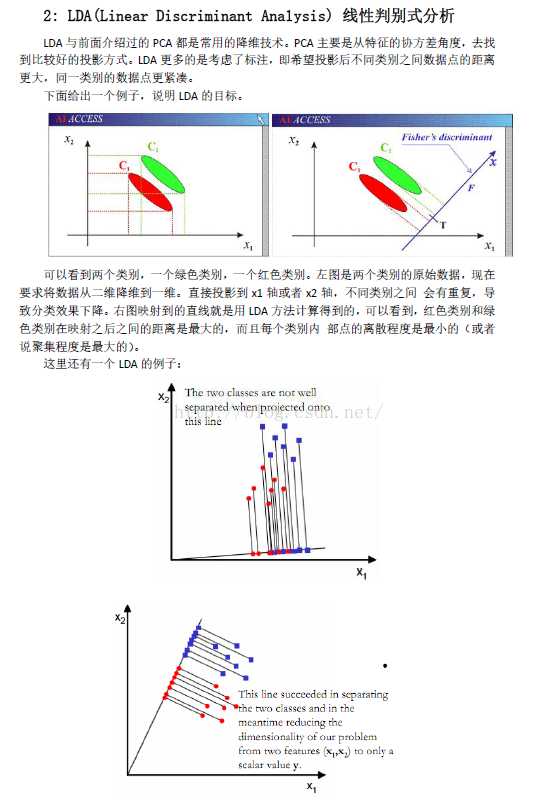
下面開始說一下LDA,  下圖來源：https://www.zhihu.com/question/34305879/answer/80372053

佔坑

PCA演算法： http://blog.csdn.net/xiaojidan2011/article/details/11595869 這個說的特別清楚，還可以補基礎

佔坑

區別：PCA是從特徵的角度協方差角度： 求出協方差矩陣的特徵值和特徵向量，然後將特徵向量按特徵值的大小排序取出前K行組成矩陣P（這個P就是我們對角化協方差矩陣的時所使用的P, 具體的可以看看矩陣對角化的過程）， 這個P就是一組正交變化基， 然後將原始的矩陣X，左乘P，也就是將X變換到P組成的正交基中，然後PX＝Y就是降維後的矩陣。 而LDA則是在已知樣本的類標註， 希望投影到新的基後使得不同的類別之間的資料點的距離更大，同一類別的資料點更緊湊。

當LDA作為一種通道補償方法時，LDA試圖找出一個新的方向能夠最小化由通道效應產生的方差,同時最大化話者間的方差,使得變換後的特徵減少通道資訊(共性資訊)，增強話者資訊(個性特徵)。這一新方向必須滿足最大化類間方差(Between-Class Variance)和最小化類內方差(Intra-Class Variance) 。

突然想起來，之前沒寫完存在草稿箱，今天逛知乎看到了，就再拿出來總結一下。