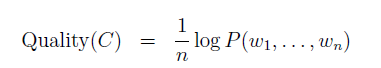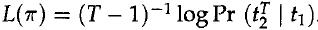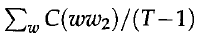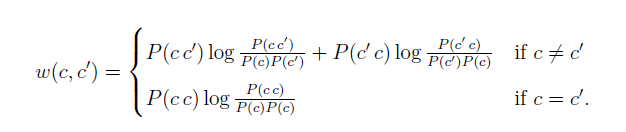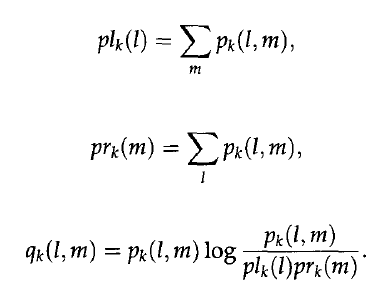Brown Clustering演算法和程式碼學習
一、演算法
布朗聚類是一種自底向上的層次聚類演算法,基於n-gram模型和馬爾科夫鏈模型。布朗聚類是一種硬聚類,每一個詞都在且只在唯一的一個類中。
w是詞,c是詞所屬的類。
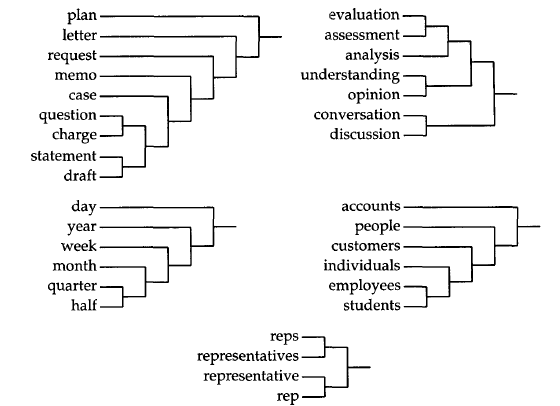
布朗聚類的輸入是一個語料庫,這個語料庫是一個詞序列,輸出是一個二叉樹,樹的葉子節點是一個個詞,樹的中間節點是我們想要的類(中間結點作為根節點的子樹上的所有葉子為類中的詞)。
初始的時候,將每一個詞獨立的分成一類,然後,將兩個類合併,使得合併之後評價函式最大,然後不斷重複上述過程,達到想要的類的數量的時候停止合併。
上面提到的評價函式,是對於n個連續的詞(w)序列能否組成一句話的概率的對數的歸一化結果。於是,得到評價函式:
n是文字長度,w是詞
上面的評價公式是PercyLiang的“Semi-supervised learning for natural languageprocessing”文章中關於布朗聚類的解釋,Browm原文中是基於class-based bigram language model建立的,於是得到下面公式:
T是文字長度,t是文字中的詞
上述公式是由於對於bigram,於是歸一化處理只需要對T-1個bigram。我覺得PercyLiang的公式容易理解評價函式的定義,但是,Brown的推導過程更加清晰簡明,所以,接下來的公式推導遵循Brown原文中的推導過程。
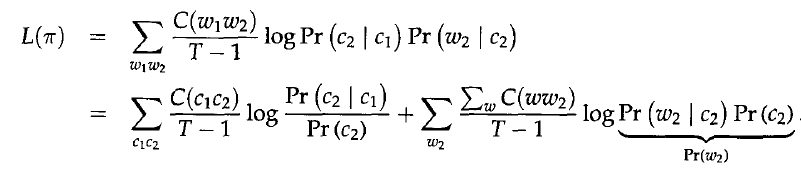
上面的推導式數學推導,接下來是一個重要的近似處理,
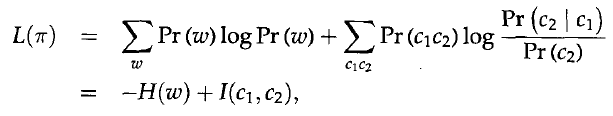
H(w)是熵,只跟1-gram的分佈有關,也就是與類的分佈無關,而I(c1,c2)是相鄰類的平均互資訊。所以,I決定了L。所以,只有最大化I,L才能最大。
二、優化
Brown提出了一種估算方式進行優化。首先,將詞按照詞頻進行排序,將前C(詞的總聚類數目)個詞分到不同的C類中,然後,將接下來詞頻最高的詞,新增到一個新的類,將(C+1)類聚類成C類,即合併兩個類,使得平均互資訊損失最小。雖然,這種方式使得計算不是特別精確,類的加入順序,決定了合併的順序,會影響結果,但是極大的降低了計算複雜度。
顯然上面提及的演算法仍然是一種naive的演算法,演算法複雜度十分高。(上述結果包括下面的複雜度結果來自Percy Liang的論文)。對於這麼高的複雜度,對於成百上千詞的聚類將變得不現實,於是,優化演算法變得不可或缺。Percy Liang和Brown分別從兩個角度去優化。
Brown從代數的角度優化,通過一個表格記錄下每次合併的中間結果,然後,用來計算下一次結果。
Percy Liang從幾何的角度考慮優化,更加清晰直觀。但是,Percy Liang是從跟Brown的損失函式L相反的角度去考慮(即兩者正負號不同),但是,都是為了保留中間結果,減少計算量,個人覺得PercyLiang的演算法比較容易理解,而且,他少忽略了一些沒必要計算的中間結果,更加優化,後面介紹的程式碼,也是PercyLiang寫的,所以,將會重點介紹一下他的思考方式。
Percy Liang將聚類結果表示成一個無向圖,圖的節點有C個,代表C個類,同時,任何兩個節點都有一條邊,邊代表相鄰兩個節點之間(兩個類之間)的平均互資訊。邊的權重如下表達式:
而評價的總的平均互資訊I就是所有邊的權重之和。下面是實際程式碼中的計算損失評價的函式即合併後的I減去合併前的I的損失。
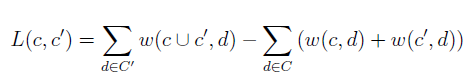
上述的(c並c')代表合併c和兩個節點後的一個節點,C是當前集合,而C'是合併後的集合:

三、程式碼實現
程式碼實現的主要過程概覽:
1、讀取文字並預處理
1) 將文字中的每個詞讀入並編碼(其中過濾一些頻次極其低的)
2)統計詞表大小、出現次數
3)將文字左右兩個方向的n-gram儲存
2、初始化布朗聚類(N log N)
1)將詞進行排序
2)將頻次最高的initC個詞分配到每個類
3)初始化p1(概率),q2(邊的權重)
3、進行布朗聚類
1)初始化L2(合併減少的互資訊)
2) 將當前未聚類的詞中,出現頻次最高的,作為一個類,新增進去,並同時,計算p1,q2,L2
3)找到最小的L2
4)合併,並更新q2,L2
程式碼還實現了計算KL散度比較相關性,此部分略去。
這裡p1如下
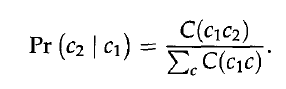
q2如下
四、重要程式碼段解析
初始化L2:
<span style="font-size:18px;">// O(C^3) time.
void compute_L2() {
track("compute_L2()", "", true);
track_block("Computing L2", "", false)
FOR_SLOT(s) {
track_block("L2", "L2[" << Slot(s) << ", *]", false)
FOR_SLOT(t) {
if(!ORDER_VALID(s, t)) continue;
double l = L2[s][t] = compute_L2(s, t);
logs("L2[" << Slot(s) << "," << Slot(t) << "] = " << l << ", resulting minfo = " << curr_minfo-l);
}
}
}</span>上面呼叫,單步計算L2:
<span style="font-size:18px;">// O(C) time.
double compute_L2(int s, int t) { // compute L2[s, t]
assert(ORDER_VALID(s, t));
// st is the hypothetical new cluster that combines s and t
// Lose old associations with s and t
double l = 0.0;
for (int w = 0; w < len(slot2cluster); w++) {
if ( slot2cluster[w] == -1) continue;
l += q2[s][w] + q2[w][s];
l += q2[t][w] + q2[w][t];
}
l -= q2[s][s] + q2[t][t];
l -= bi_q2(s, t);
// Form new associations with st
FOR_SLOT(u) {
if(u == s || u == t) continue;
l -= bi_hyp_q2(_(s, t), u);
}
l -= hyp_q2(_(s, t)); // q2[st, st]
return l;
}
</span>聚類過程中,更新p1,q2,L2,呼叫時(兩次):
<span style="font-size:18px;">// Stage 1: Maintain initC clusters. For each of the phrases initC..N-1, make
// it into a new cluster. Then merge the optimal pair among the initC+1
// clusters.
// O(N*C^2) time.
track_block("Stage 1", "", false) {
mem_tracker.report_mem_usage();
for(int i = initC; i < len(freq_order_phrases); i++) { // Merge phrase new_a
int new_a = freq_order_phrases[i];
track("Merging phrase", i << '/' << N << ": " << Cluster(new_a), true);
logs("Mutual info: " << curr_minfo);
incorporate_new_phrase(new_a);//新增後,C->C+1
repcheck();
merge_clusters(find_opt_clusters_to_merge());//合併後,C+1->C
repcheck();
}
}
</span>新增後,更新p1,q2,L2
<span style="font-size:18px;">// Add new phrase as a cluster.
// Compute its L2 between a and all existing clusters.
// O(C^2) time, O(T) time over all calls.
void incorporate_new_phrase(int a) {
track("incorporate_new_phrase()", Cluster(a), false);
int s = put_cluster_in_free_slot(a);
init_slot(s);
cluster2rep[a] = a;
rep2cluster[a] = a;
// Compute p1
p1[s] = (double)phrase_freqs[a] / T;
// Overall all calls: O(T)
// Compute p2, q2 between a and everything in clusters
IntIntMap freqs;
freqs.clear(); // right bigrams
forvec(_, int, b, right_phrases[a]) {
b = phrase2rep.GetRoot(b);
if(!contains(rep2cluster, b)) continue;
b = rep2cluster[b];
if(!contains(cluster2slot, b)) continue;
freqs[b]++;
}
forcmap(int, b, int, count, IntIntMap, freqs) {
curr_minfo += set_p2_q2_from_count(cluster2slot[a], cluster2slot[b], count);
logs(Cluster(a) << ' ' << Cluster(b) << ' ' << count << ' ' << set_p2_q2_from_count(cluster2slot[a], cluster2slot[b], count));
}
freqs.clear(); // left bigrams
forvec(_, int, b, left_phrases[a]) {
b = phrase2rep.GetRoot(b);
if(!contains(rep2cluster, b)) continue;
b = rep2cluster[b];
if(!contains(cluster2slot, b)) continue;
freqs[b]++;
}
forcmap(int, b, int, count, IntIntMap, freqs) {
curr_minfo += set_p2_q2_from_count(cluster2slot[b], cluster2slot[a], count);
logs(Cluster(b) << ' ' << Cluster(a) << ' ' << count << ' ' << set_p2_q2_from_count(cluster2slot[b], cluster2slot[a], count));
}
curr_minfo -= q2[s][s]; // q2[s, s] was double-counted
// Update L2: O(C^2)
track_block("Update L2", "", false) {
the_job.s = s;
the_job.is_type_a = true;
// start the jobs
for (int ii=0; ii<num_threads; ii++) {
thread_start[ii].unlock(); // the thread waits for this lock to begin
}
// wait for them to be done
for (int ii=0; ii<num_threads; ii++) {
thread_idle[ii].lock(); // the thread releases the lock to finish
}
}
//dump();
}
</span>合併後,更新
<span style="font-size:18px;">// O(C^2) time.
// Merge clusters a (in slot s) and b (in slot t) into c (in slot u).
void merge_clusters(int s, int t) {
assert(ORDER_VALID(s, t));
int a = slot2cluster[s];
int b = slot2cluster[t];
int c = curr_cluster_id++;
int u = put_cluster_in_free_slot(c);
free_up_slots(s, t);
// Record merge in the cluster tree
cluster_tree[c] = _(a, b);
curr_minfo -= L2[s][t];
// Update relationship between clusters and rep phrases
int A = cluster2rep[a];
int B = cluster2rep[b];
phrase2rep.Join(A, B);
int C = phrase2rep.GetRoot(A); // New rep phrase of cluster c (merged a and b)
track("Merging clusters", Cluster(a) << " and " << Cluster(b) << " into " << c << ", lost " << L2[s][t], false);
cluster2rep.erase(a);
cluster2rep.erase(b);
rep2cluster.erase(A);
rep2cluster.erase(B);
cluster2rep[c] = C;
rep2cluster[C] = c;
// Compute p1: O(1)
p1[u] = p1[s] + p1[t];
// Compute p2: O(C)
p2[u][u] = hyp_p2(_(s, t));
FOR_SLOT(v) {
if(v == u) continue;
p2[u][v] = hyp_p2(_(s, t), v);
p2[v][u] = hyp_p2(v, _(s, t));
}
// Compute q2: O(C)
q2[u][u] = hyp_q2(_(s, t));
FOR_SLOT(v) {
if(v == u) continue;
q2[u][v] = hyp_q2(_(s, t), v);
q2[v][u] = hyp_q2(v, _(s, t));
}
// Compute L2: O(C^2)
track_block("Compute L2", "", false) {
the_job.s = s;
the_job.t = t;
the_job.u = u;
the_job.is_type_a = false;
// start the jobs
for (int ii=0; ii<num_threads; ii++) {
thread_start[ii].unlock(); // the thread waits for this lock to begin
}
// wait for them to be done
for (int ii=0; ii<num_threads; ii++) {
thread_idle[ii].lock(); // the thread releases the lock to finish
}
}
}
void merge_clusters(const IntPair &st) { merge_clusters(st.first, st.second); }
</span>更新L2過程,其中使用了多執行緒:
使用資料結構:
<span style="font-size:18px;">// Variables used to control the thread pool
mutex * thread_idle;
mutex * thread_start;
thread * threads;
struct Compute_L2_Job {
int s;
int t;
int u;
bool is_type_a;
};
Compute_L2_Job the_job;
bool all_done = false;
</span>初始化,將所有執行緒鎖住:
<span style="font-size:18px;">// start the threads
thread_start = new mutex[num_threads];
thread_idle = new mutex[num_threads];
threads = new thread[num_threads];
for (int ii=0; ii<num_threads; ii++) {
thread_start[ii].lock();
thread_idle[ii].lock();
threads[ii] = thread(update_L2, ii);
}
</span><span style="font-size:18px;">// Update L2: O(C^2)
track_block("Update L2", "", false) {
the_job.s = s;
the_job.is_type_a = true;
// start the jobs
for (int ii=0; ii<num_threads; ii++) {
thread_start[ii].unlock(); // the thread waits for this lock to begin
}
// wait for them to be done
for (int ii=0; ii<num_threads; ii++) {
thread_idle[ii].lock(); // the thread releases the lock to finish
}
}
</span>第二處是在合併後
<span style="font-size:18px;">// Compute L2: O(C^2)
track_block("Compute L2", "", false) {
the_job.s = s;
the_job.t = t;
the_job.u = u;
the_job.is_type_a = false;
// start the jobs
for (int ii=0; ii<num_threads; ii++) {
thread_start[ii].unlock(); // the thread waits for this lock to begin
}
// wait for them to be done
for (int ii=0; ii<num_threads; ii++) {
thread_idle[ii].lock(); // the thread releases the lock to finish
}
}
</span>結束呼叫:
<span style="font-size:18px;">// finish the threads
all_done = true;
for (int ii=0; ii<num_threads; ii++) {
thread_start[ii].unlock(); // thread will grab this to start
threads[ii].join();
}
delete [] thread_start;
delete [] thread_idle;
delete [] threads;
</span>參考文獻:
Liang: Semi-supervised learning for natural language processing
Brown, et al.: Class-Based n-gram Models of Natural Language
程式碼來源:
https://github.com/percyliang/brown-cluster