區域性線性嵌入(Locally Linear Embedding，以下簡稱LLE)也是非常重要的降維方法。和傳統的PCA，LDA等關注樣本方差的降維方法相比，LLE關注於降維時保持樣本區域性的線性特徵，由於LLE在降維時保持了樣本的區域性特徵，它廣泛的用於影象影象識別，高維資料視覺化等領域。下面我們就對LLE的原理做一個總結。

1. 流形學習概述

　　　　LLE屬於流形學習(Manifold Learning)的一種。因此我們首先看看什麼是流形學習。流形學習是一大類基於流形的框架。數學意義上的流形比較抽象，不過我們可以認為LLE中的流形是一個不閉合的曲面。這個流形曲面有資料分佈比較均勻，且比較稠密的特徵，有點像流水的味道。基於流行的降維演算法就是將流形從高維到低維的降維過程，在降維的過程中我們希望流形在高維的一些特徵可以得到保留。

　　　　一個形象的流形降維過程如下圖。我們有一塊捲起來的布，我們希望將其展開到一個二維平面，我們希望展開後的布能夠在區域性保持布結構的特徵，其實也就是將其展開的過程，就想兩個人將其拉開一樣。

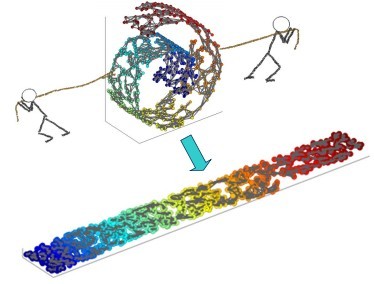
　　　　在區域性保持布結構的特徵，或者說資料特徵的方法有很多種，不同的保持方法對應不同的流形演算法。比如等距對映（ISOMAP）演算法在降維後希望保持樣本之間的測地距離而不是歐式距離，因為測地距離更能反映樣本之間在流形中的真實距離。

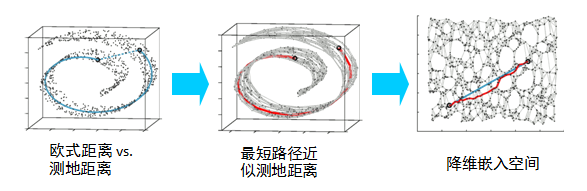
　　　　但是等距對映演算法有一個問題就是他要找所有樣本全域性的最優解，當資料量很大，樣本維度很高時，計算非常的耗時，鑑於這個問題，LLE通過放棄所有樣本全域性最優的降維，只是通過保證區域性最優來降維。同時假設樣本集在區域性是滿足線性關係的，進一步減少的降維的計算量。

2. LLE思想

　　　　現在我們來看看LLE的演算法思想。

　　　　LLE首先假設資料在較小的區域性是線性的，也就是說，某一個數據可以由它鄰域中的幾個樣本來線性表示。比如我們有一個樣本x1x1,我們在它的原始高維鄰域裡用K-近鄰思想找到和它最近的三個樣本x2,x3,x4x2,x3,x4. 然後我們假設x1x1可以由x2,x3,x4x2,x3,x4線性表示，即：

x1=w12x2+w13x3+w14x4x1=w12x2+w13x3+w14x4

　　　　其中，w12，w13，w14w12，w13，w14為權重係數。在我們通過LLE降維後，我們希望x1x1在低維空間對應的投影x

′1x1′和x2,x3,x4x2,x3,x4對應的投影x′2,x′3,x′4x2′,x3′,x4′也儘量保持同樣的線性關係，即

x′1≈w12x′2+w13x′3+w14x′4x1′≈w12x2′+w13x3′+w14x4′

　　　　也就是說，投影前後線性關係的權重係數w12，w13，w14w12，w13，w14是儘量不變或者最小改變的。

　　　　從上面可以看出，線性關係只在樣本的附近起作用，離樣本遠的樣本對區域性的線性關係沒有影響，因此降維的複雜度降低了很多。

　　　　下面我們推導LLE演算法的過程。

3. LLE演算法推導

　　　　對於LLE演算法，我們首先要確定鄰域大小的選擇，即我們需要多少個鄰域樣本來線性表示某個樣本。假設這個值為k。我們可以通過和KNN一樣的思想通過距離度量比如歐式距離來選擇某樣本的k個最近鄰。

　　　　在尋找到某個樣本的

相關推薦

區域性線性嵌入(LLE)原理總結

　區域性線性嵌入(Locally Linear Embedding，以下簡稱LLE)也是非常重要的降維方法。和傳統的PCA，LDA等關注樣本方差的降維方法相比，LLE關注於降維時保持樣本區域性的線性特徵，由於LLE在降維時保持了樣本的區域性特徵，它廣泛的用於影象影象識

用scikit-learn研究區域性線性嵌入(LLE)

　　　　在區域性線性嵌入(LLE)原理總結中，我們對流形學習中的區域性線性嵌入(LLE)演算法做了原理總結。這裡我們就對scikit-learn中流形學習的一些演算法做一個介紹，並著重對其中LLE演算法的使用方法做一個實踐上的總結。 1. scikit-learn流形學習庫

LLE((locally linear embedding) 區域性線性嵌入演算法，一種降維方法

原始特徵的數量可能很大，或者說樣本是處於一個高維空間中，通過對映或變換的方法，降高維資料降低到低維空間中的資料，這個過程叫特徵提取，也稱降維。    特徵提取得基本任務研究從眾多特徵中求出那些對分類最有效的特徵，從而實現特徵空間維數的壓縮。傳統的降維技術可以分為線性和

主成分分析(PCA)和區域性線性嵌入（LEE）原理詳解

k近鄰 k鄰近學習是一種常用的監督學習。其工作機制:給定測試樣本，基於某種度量找出與測試樣本最靠近的K個訓練樣本，在分類任務中是基於K個“鄰居”樣本的類別投票法來確定測試樣本的類別，在迴歸任務中是基於K個“鄰居”樣本輸出標記的平均值作為預測結果。 k鄰近學習

LLE原理總結

區域性線性嵌入(Locally Linear Embedding，以下簡稱LLE)也是非常重要的降維方法。和傳統的PCA，LDA等關注樣本方差的降維方法相比，LLE關注於降維時保持樣本區域性的線性特徵，由於LLE在降維時保持了樣本的區域性特徵，它廣泛的用於影象影象識別

降維演算法（LASSO、PCA、聚類分析、小波分析、線性判別分析、拉普拉斯特徵對映、區域性線性嵌入）

1、LASSO LASSO全稱least absolute shrinkage and selection operator，本身是一種迴歸方法。與常規迴歸方法不同的是，LASSO可以對通過引數縮減對引數進行選擇，從而達到降維的目的。說到LASSO，就不得不說

區域性線性嵌入降維演算法（含實驗程式碼）

區域性線性嵌入演算法（Locally linear embedding, LLE）是一個非線性降維方法，由 Sam T.Roweis 和Lawrence K.Saul 於 2000 年提出並發表在《Science》雜誌上。它能夠使降維後的資料保持原有拓撲結構不變。現在已經

線性判別分析LDA原理總結

　在主成分分析（PCA）原理總結中，我們對降維演算法PCA做了總結。這裡我們就對另外一種經典的降維方法線性判別分析（Linear Discriminant Analysis, 以下簡稱LDA）做一個總結。LDA在模式識別領域（比如人臉識別，艦艇識別等圖形影象識別領域）中有非常

『理論』科學計算專項_線性代數幾何原理剖析

str tar 是否 數學 這就是 cti bsp 存在 amp 矩陣左乘向量的兩種理解 1，矩陣左乘向量可以理解為對向量進行線性變換 探究原理的話，可以理解左乘為對整個空間（基&目標向量）進行線性變換，其中， 變換矩陣是基‘在基的坐標的列向量組合 目標向量是向量

Synchronized實現原理總結

依次 mark adding ali zed 線程id 遍歷 安全 ren synchronized實現同步的基礎：Java中的每一個對象都可以作為鎖。具體表現為以下3種形式。對於普通同步方法，鎖是當前實例對象。對於靜態同步方法，鎖是當前類的Class對象。對於同步方法塊，

orcFile split和讀數據原理總結（hive0.13）

etime cit .net ack 處理 gem gravity AC col http://blog.csdn.net/zhaorongsheng/article/details/72903431 官網關於orcfile的介紹 背景 Hive的rcfile格式已經使

CRC原理總結

加密算法 info 結果 alt 附加 序列 註意 選擇 二進制序列 CRC常用於判斷文件在傳輸過程中文件內容是否被更改以及其他的一些加密算法，在Java中，CRC32 工具類提供給我們使用。 1.CRC校驗具體原理如下： 　　在要發送的數據幀後面附加一個數（這個就是用來校

Android - View繪圖原理總結

繼承 最終 操作 地方 margin mea 類型 滾動條 gin Android系統的視圖結構的設計也采用了組合模式，即View作為所有圖形的基類，Viewgroup對View繼承擴展為視圖容器類，由此就得到了視圖部分的基本結構--樹形結構 View定義了繪圖的基本操作

iOS底層原理總結 - 探尋block的本質（一）

release nss 命令 static 斷點 fix 生成 什麽是 block類型 面試題 block的原理是怎樣的？本質是什麽？ __block的作用是什麽？有什麽使用註意點？ block的屬性修飾詞為什麽是copy？使用block有哪些使用

《編譯原理總結》

研究 yacc 語義檢查 裏的 思維 概念 and 靜態 後來 Decaf編譯器（mind語言） PL/0編譯器 構造工具：lex yacc 單遍編譯器 類p-code虛擬機 學編譯是學的相關的思想和研究，科研和教學還是有不同目的的 抽象語法樹AST 三地址碼TA

受限玻爾茲曼機（RBM）原理總結

guid filter font list cuc spa 得到 aci dcb https://blog.csdn.net/l7H9JA4/article/details/81463954 授權轉發自：劉建平《受限玻爾茲曼機（RBM）原理總結》 地址:http://w

spark啟動原理總結

lead term 技術 forward deploy ddp rbo 其他 sso 一般情況下，我們啟動spark集群都是start-all.sh或者是先啟動master(start-master.sh),然後在啟動slave節點(start-slaves.sh)，其實翻

linux下DHCP服務原理總結

relay 解析 over eth eas data- false security 設置 linux下DHCP服務 DHCP（全稱Dynamic host configuration protocol）：動態主機配置協議 DHCP工作在OSI的應用層，可以幫助計算機從指定

Kafka史上最詳細原理總結

send shu control 並保存 分布 batch 重傳 應該 還要 Kafka是最初由Linkedin公司開發，是一個分布式、支持分區的（partition）、多副本的（replica），基於zookeeper協調的分布式消息系統，它的最大的特性就是可以實時的處理

特徵值法解常係數線性微分方程解法總結

1. 引言 2. 準備知識 3. 常係數齊次線性微分方程和尤拉方程 3.1 常係數齊次線性微分方程的解 3.2 Euler方程 4. 非齊次線性微分方程(比較係數法) 4.