主成分分析(PCA)和區域性線性嵌入(LEE)原理詳解
阿新 • • 發佈:2019-02-05
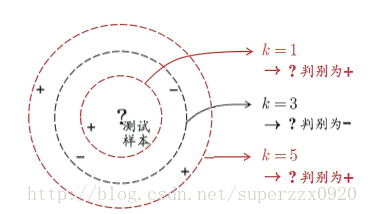
k近鄰
k鄰近學習是一種常用的監督學習。其工作機制:給定測試樣本,基於某種度量找出與測試樣本最靠近的K個訓練樣本,在分類任務中是基於K個“鄰居”樣本的類別投票法來確定測試樣本的類別,在迴歸任務中是基於K個“鄰居”樣本輸出標記的平均值作為預測結果。
k鄰近學習缺陷與優點
- k鄰近稱為“懶惰學習”:訓練階段僅僅儲存訓練樣本,訓練時間開銷為0,待收到測試樣本後才進行學習
- 不同距離計算導致不同的結果”
- 假設樣本獨立同分布 ,對任意x和任意小整數a,在x的附近a距離總能找到一個訓練樣本z。則
c∗=argmaxxϵYP(c|x) 表示貝葉斯最優分類器。經過推導可以得到K近鄰泛化錯誤不超過貝葉斯最優分類器的2倍。想要維持K鄰近低範化錯誤,則訓練樣本密度必須足夠大。對於高維而言,若每一個屬性維度的訓練樣本的密度都很大,這會導致訓練樣本數量急劇增加,就出現了’維數災難‘。
主成分分析PCA
PCA是一種對原始高維空間進行線性變換從而獲得低維空間,並期望在所投影的維度上資料的方差最大,以此使用較少的資料維度,同時保留住較多的原資料點的特性。
需要注意PCA屬於特徵抽取不屬於特徵選擇。給定d維空間中的樣本
幫助理解這裡有小插曲
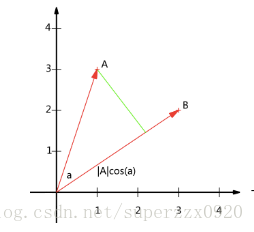
- A⋅B=|A||B|cos(a) A與B的內積等於A到B的投影長度乘以B的模。
設向量B的模為1,A⋅B=|A|cos(a),則A與B的內積值等於A向B所在直線投影的向量長度
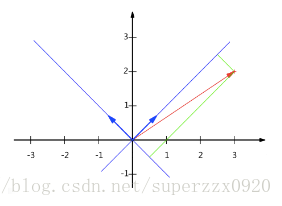
要準確描述向量,首先要確定一組基,然後給出在基所在的各個直線上的投影值
- 在直角座標系中的向量(x,y)實際上表示線性組合:x(1,0)T+y(0,1)T
- 兩個矩陣相乘的意義是將右邊矩陣中的每一列列向量變換到左邊矩陣中每一行行向量為基所表示的空間中去
根據以上的預備知識可以理解原屬性
現在進入正題,對於正交屬性的空間中的樣本點,如何用一個超平面(直線的高維推廣)對所有樣本進行恰當的表達?
- 最近重構性:樣本點到這個平面的距離都足夠近
- 最大可分性:樣本點在這個超平面的投影都儘可能分開
最近重構性和最大可分性可以得到兩種主成分的等價推導,以下推導是從最近重構性角度來出發。
- 假定樣本進行了中心化即
∑xi=0 - 變換座標為W=
(w1,w2,...wm) ,其中wi 是標準正交基–∥wi∥2=1 ,wTiwj=0i≠j - 設將維度降低到d’,樣本點
xi→ 在低維座標中的投影zi→=(zi1;zi2...zid′) 其中zij=wTi→xj→ 是xi 在低維座標系的第j維投影 - 基於低維樣本
zi 重構xi ,重構後的每個樣本點來說xi^=∑d′j=1zijwj→ 。重構的意思低維新空間的座標與基做內積
原樣本點

- 其中
x