通常情況下，在不均衡學習應用中使用抽樣方法的目的就是為了通過一些機制改善不均衡資料集，以期獲得一個均衡的資料分佈。

研究表明，對於一些基分類器來說，與不均衡的資料集相比一個均衡的資料集可以提高全域性的分類效能。資料層面的處理方法是處理不均衡資料分類問題的重要途徑之一，它的實現方法主要分為對多數類樣本的欠抽樣和對少數類樣本的過抽樣學習兩種。其主要思想是通過合理的刪減或者增加一些樣本來實現資料均衡的目的，進而降低資料不均衡給分類器帶來的負面影響。

按照對樣本數量的影響又可分為：

• 過抽樣，即合理地增加少數類的樣本
• 欠抽樣，即合理地刪減多數類樣本

隨機過抽樣和欠抽樣

隨機過抽樣

隨機過抽樣是一種按照下面的描述從少數類中速記抽樣生成子集合 E 的方法。

1. 首先在少數類 SminSmin 集合中隨機選中一些少數類樣本
2. 然後通過複製所選樣本生成樣本集合 E
3. 將它們新增到 SminSmin 中來擴大原始資料集從而得到新的少數類集合 Smin−newSmin−new

用這樣方法，SminSmin 中的總樣本數增加了 |E||E| 個新樣本，且 Smin−newSmin−new 的類分佈均衡度進行相應的調整，如此操作可以改變類分佈平衡度從而達到所需水平。

欠抽樣

欠抽樣技術是將資料從原始資料集中移除。

1. 首先我們從 SmajSmaj 中隨機地選取一些多數類樣本 E
2. 將這些樣本從 SmajSmaj 中移除，就有 |Smaj−new|=|Smaj|−|E||Smaj−new|=|Smaj|−|E|

缺陷

初看，過抽樣和欠抽樣技術在功能上似乎是等價的，因為它們都能改變原始資料集的樣本容量且能夠獲得一個相同比例的平衡。

但是，這個共同點只是表面現象，這是因為這兩種方法都將會產生不同的降低分類器學習能力的負面效果。

• 對於欠抽樣演算法，將多數類樣本刪除有可能會導致分類器丟失有關多數類的重要資訊。
• 對於過抽樣演算法，雖然只是簡單地將複製後的資料新增到原始資料集中，且某些樣本的多個例項都是“並列的”，但這樣也可能會導致分類器學習出現過擬合現象，對於同一個樣本的多個複本產生多個規則條例，這就使得規則過於具體化；雖然在這種情況下，分類器的訓練精度會很高，但在位置樣本的分類效能就會非常不理想。

informed 欠抽樣

兩個 informed 欠抽樣演算法：EasyEnsemble 和 BalanceCascade 演算法，這兩種方法克服了傳統隨機欠抽樣方法導致的資訊缺失的問題，且表現出較好的不均衡資料分類效能。

EasyEnsemble 和 BalanceCascade 演算法介紹【接下來詳細研究這倆方法】

1. EasyEnsemble 核心思想是：

• 首先通過從多數類中獨立隨機抽取出若干子集
• 將每個子集與少數類資料聯合起來訓練生成多個基分類器
• 最終將這些基分類器組合形成一個整合學習系統

EasyEnsemble 演算法被認為是非監督學習演算法，因此它每次都獨立利用可放回隨機抽樣機制來提取多數類樣本

2. BalanceCascade 核心思想是：

• 使用之前已形成的整合分類器來為下一次訓練選擇多類樣本
• 然後再進行欠抽樣

最近鄰規則（ENN）

因為隨機欠抽樣方法未考慮樣本的分佈情況，取樣具有很大的隨機性，可能會刪除重要的多數類樣本資訊。針對以上的不足，Wilson 等人提出了一種最近鄰規則(edited nearest neighbor: ENN)。

• 基本思想：刪除那些類別與其最近的三個近鄰樣本中的兩個或兩個以上的樣本類別不同的樣本
• 缺點：因為大多數的多數類樣本的樣本附近都是多數類，所以該方法所能刪除的多數類樣本十分有限。

領域清理規則 (NCL)

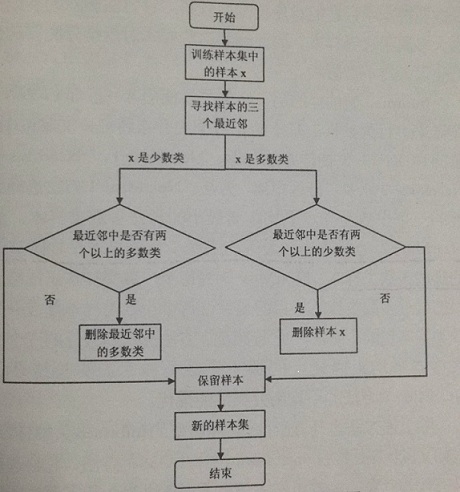
Laur Ikkala J 等人在 ENN 的基礎行提出了 領域清理規則 (neighborhod cleaning rule: NCL)。該演算法的整體流程圖如下所示：

• 主要思想：針對訓練樣本集中的每個樣本找出其三個最近鄰樣本，若該樣本是多數類樣本且其三個最近鄰中有兩個以上是少數類樣本，則刪除它；反之當該樣本是少數類並且其三個最近鄰中有兩個以上是多數類樣本，則去除近鄰中的多數類樣本。
• 缺陷：未能考慮到在少數類樣本中存在的噪聲樣本而且第二種方法刪除的多數類樣本大多屬於邊界樣本，刪除這些樣本，對後續分類器的分類產生很大的不良影響。

K-近鄰（KNN）

基於給定資料的分佈特徵，有四種 KNN 欠抽樣方法：

1. NearMiss-1 
選擇到最近的三個少數類樣本平均距離最小的那些多數類樣本

2. NearMiss-2 
選擇到最遠的三個少數類樣本平均距離最小的那些多數類樣本

3. NearMiss-3 
為每個少數類樣本選擇給定數目的最近多數類樣本，目的是保證每個少數類樣本都被一些多數類樣本包圍

4. 最遠距離 
選擇到最近的三個少數類樣本平均距離最大的那些多數類樣本

Note：實驗結果表明 NearMiss-2 方法的不均衡分類效能最優

資料生成的合成抽樣方法

在合成抽樣技術方面， Chawla NV 等人提出的 SMOTE 過抽樣技術是一個強有力的方法。SMOTE 過抽樣技術與傳統的簡單樣本複製的過抽樣方法不同，它是利用少數類樣本控制人工樣本的生成與分佈，實現資料集均衡的目的，而且該方法可以有效地解決由於決策區間較小導致的分類過擬合問題。

SMOTE 演算法是利用特徵空間中現存少數類樣本之間的相似性來建立人工資料的。特別是，對於子集 Smin⊂SSmin⊂S ，對於每一個樣本 xi⊂Sminxi⊂Smin 使用 K-近鄰法，其中 K 是某些制定的整數。

這裡 K-近鄰 被定義為考慮 SminSmin 中的 K 個元素本身與 xixi 的歐氏距離在 n 維特徵空間 X 中表現為最小幅度值的樣本。為了構建一個合成樣本

1. 首先隨機選擇一個 K-近鄰
2. 然後用在 [0,1] 之間的隨機數乘以對應特徵向量的差異
3. 最後再加上 xixi

xnew=xi+(x̂ i−xi)∗δxnew=xi+(x^i−xi)∗δ

其中 xi⊂Sminxi⊂Smin 是當前少數類樣本，x̂ ix^i 是 xixi 的一個 K-近鄰（隨機）：x̂ i⊂Sminx^i⊂Smin，且 δϵ[0,1]δϵ[0,1] 是一個隨機數。因此，根據上式產生的合成樣本是與所考慮的點 xixi 在同一條線段上，且 xixi 是隨機選取的。

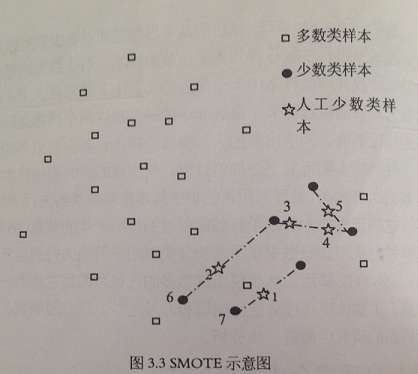
以下是 SMOTE 過程的一個例子，K=6

、、

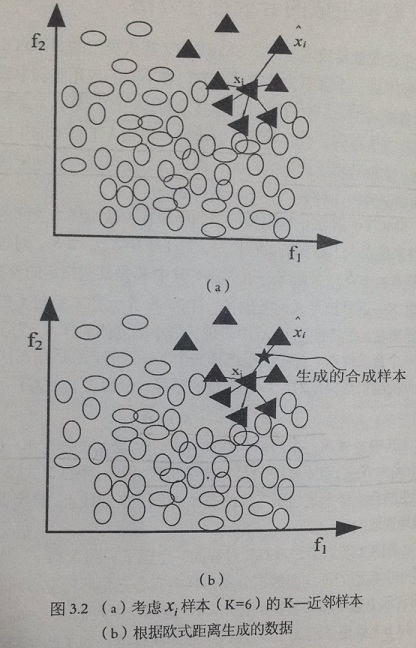
可以看出 SMOTE 演算法是建立在相距較近的少數類樣本之間的樣本仍然是少數類的假設基礎上的。

1. 總結

• 對於少數類的每個樣本尋找其同類樣本中 k 個最近鄰。其中，k 通常是大於 1 的奇數
• 重複上述插值過程，使得新生成的訓練資料集資料達到均衡，最後利用新的訓練樣本集進行訓練

2. 優點

• 有助於簡單打破過抽樣所產生的關係
• 使得分類器的學習能力得到顯著提高

3. 缺陷

• 體現在過分泛化問題和方差

自適應合成抽樣方法

Borderline-SMOTE 演算法介紹

在 SMOTE 演算法中，過度泛化問題主要歸結於產生合成樣本的方法。特別是，SMOTE 演算法對於每個原少數類樣本產生相同數量的合成數據樣本，而沒有考慮其鄰近樣本的分佈特點，這就使得類間發生重複的可能性加大。

從前面介紹的 SMOTE 演算法原理，結合下圖發現，SMOTE 演算法產生新的人工少數類樣本過程時，只是簡單地在同類近鄰之間插值，並沒有考慮到少數類樣本週圍多數類樣本的分佈情況。如下圖

上圖中，圓點 6 和 7 分佈在多數類樣本週圍，它們和其他樣本生成的人工少數類樣本 1 和 2 離多數類樣本最近，這就導致它們有可能被劃分成多數類樣本。因而從圖中可以看出，SMOTE 演算法的樣本生成機制存在著一定盲目性

為了克服這個限制，多種不同的自適應抽樣方法相繼被提出，其中具有代表性的演算法包括 Borderline-SMOTE 演算法 和 自適應合成抽樣演算法 (ADASYN)。

Borderline-SMOTE 演算法步驟

對於這些自適應演算法，我們最感興趣的就是用於識別少數類種子樣本的方法。在 Borderline-SMOTE 演算法 中，識別少數類種子樣本的過程如下：

1. 首先，對於每個 xi⊂Sminxi⊂Smin 確定一系列最近鄰樣本集，稱該資料集為 Si:m−NNSi:m−NN，且 Si:m−NN⊂SSi:m−NN⊂S
2. 然後，對每個樣本 xixi ，判斷出最近鄰樣本集中屬於多數類樣本的個數，即：|Si:m−NN⋂Smaj||Si:m−NN⋂Smaj|
3. 最後，選擇滿足下面不等式的 xixi：m2<|Si:m−NN⋂Smaj|<mm2<|Si:m−NN⋂Smaj|<m

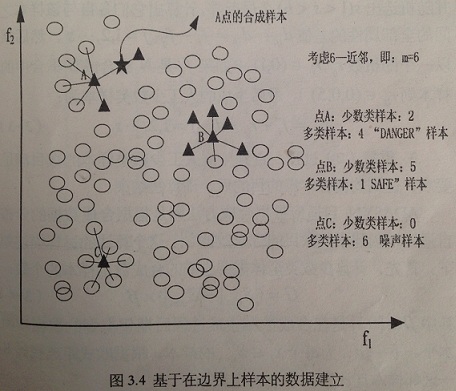
上式表明，只有最近鄰樣本集中多數類對於少數類的那些 xixi 才會被選中形成 “危險集 (DANGER)”。因此，DANGER 集中的樣本代表少數類樣本的邊界（最容易被錯分的樣本）。然後對 DANGER 集使用 SMOTE 演算法來在邊界附近產生人工合成少數類樣本

我們注意到，如果 |Si:m−NN⋂Smaj|=m|Si:m−NN⋂Smaj|=m，即： xixi 的所有 m 個最近鄰樣本都屬於多類，像下圖所示的樣本 C

那麼，我們就認為樣本 xixi 是噪聲且它不能生成合成樣本。上圖也給出了一個樣本的 Borderline-SMOTE 演算法的過程。

比較圖 3.3 和 3.4 ，我們發現 SMOTE 和 Borderline-SMOTE 演算法最大的不同就是：SMOTE 演算法為每一個少數類樣本生成合成樣本，然而 Borderline-SMOTE 演算法只為那些 “靠近” 邊界的少數類樣本生成合成樣本

Borderline-SMOTE 流程圖

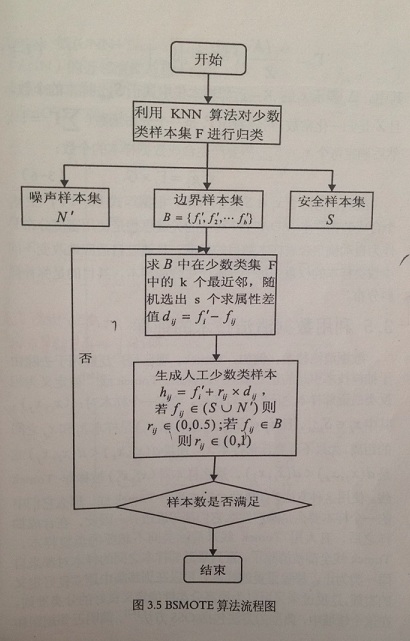
如圖，Borderline-SMOTE 演算法具體描述如下：文中訓練樣本集為 T，少數類樣本 F={f1,f2,...,fn}F={f1,f2,...,fn}

（1） 步驟一 
1. 計算少數類樣本集 F 中每一個樣本在訓練樣本集 T 中的 k 個最近鄰 
2. 然後根據這 k 個最近鄰對 F 中的樣本進行歸類：

• 假設這 k 個最近鄰都是多數類樣本，則我們將該樣本定義為噪聲樣本，將它放在 N′N′ 集合中
• 反之 k 個最近鄰都是少數類樣本則該樣本是遠離分類邊界，將其放入 S 集合中
• 最後 k 個最近鄰既有多數類樣本又有少數類樣本，則認為是邊界樣本，放入 B 集合中

（2）步驟二 
1. 設邊界樣本集 B={f1′,f2′,...,fb′}B={f1′,f2′,...,fb′}，計算 B 集合中的每一個樣本 fi′,i=1,2,...,bfi′,i=1,2,...,b 在少數類樣本 F 中的 k′k′ 個最近鄰 fijfij 
2. 隨機選出 s(1<s<b)s(1<s<b) 個最近鄰 
3. 計算出它們各自與該樣本之間的全部屬性的差值 dij：dij=fi′−fij，j=1,2,...,sdij：dij=fi′−fij，j=1,2,...,s 
4. 然後乘以一個隨機數 rij，rij∈(0,1)rij，rij∈(0,1)（如果 fijfij 是 N′N′ 集合或 S集合中的樣本，則 rij∈(0,0.5)rij∈(0,0.5) 
5. 最後生成的人工少數類樣本為：hij=fi′+rij∗dij,j=1,2,...,shij=fi′+rij∗dij,j=1,2,...,s

（3）步驟三 
重複步驟 2 過程，直到生成人工少數類樣本的數目滿足要求，達到均衡樣本集的目的後，則演算法結束

利用資料清洗技術的抽樣

資料清洗技術，例如：Tomek ，現已廣泛應用於去除由於抽樣技術引起的重複項。

• 定義：Tomek 線被定義為相反類最近鄰樣本之間的一對連線
• 符號約定：給定一個樣本對：(xi,xj)(xi,xj)，其中 xi∈Sminxi∈Smin ，且 xj∈Smajxj∈Smaj，記 d(xi,xj)d(xi,xj) 是樣本 xixi 和 xjxj 之間的距離
• 公式表示：如果不存在任何樣本 xkxk，使得 d(xi,xk)<d(xi,xj)d(xi,xk)<d(xi,xj) 或 d(xj,xk)<d(xi,xj)d(xj,xk)<d(xi,xj)，那麼樣本對 (xi,xj)(xi,xj)被稱為 Tomek 線

使用這種方法，如果兩個樣本來自 Tomek 線，那麼他們中的一個樣本要麼是噪聲要麼它們都鄰近邊界。因此，在合成抽樣之後，有人用 Tomek 線來清除類間不想要的重複樣本，Tomek 線都被清除了，直到最近鄰樣本之間的樣本對都來之同一類為止。

移除重複的樣本，可以在訓練集中建立良號定義的類簇，這反過來又可以為提高分類效能定義良好的分類準則。在這個領域中，典型的方法包括 OSS 方法、簡明近鄰規則、Tomek線（CNN+Tomek）整合方法、基於編輯近鄰（ENN）的近鄰 清理規則（NCL）、SMOTE 和ENN 的整合（SMOTE+ENN）以及 SMOTE 與 Tomek 線的整合（SMOTE+Tomek）。

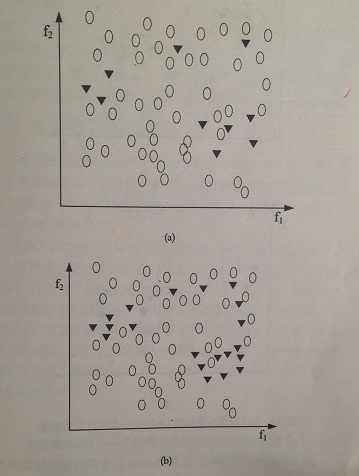
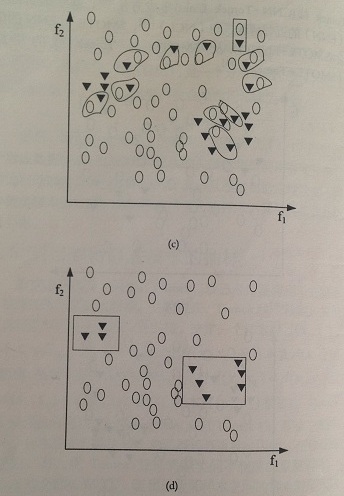
(a) 原資料集分佈　　　　　　　　　　　　　　　　 (c) 被識別出的 Tomek 線 
(b) Post-SMOTE 資料集　　　　　　　　　　　　　(d) 移除 Tomek 線後的資料集

上圖給出了將 SMOTE 和 Tomek 結合起來來清理重複資料點的典型過程。

• 圖(a) 給出了一個人工不均衡資料集的原始集分佈。注意存在於少數類和多類之間的原有重複點。
• 圖(b) 給出了使用 SMOTE 演算法生成合成樣本之後的資料集分佈。可以看出，使用 SMOTE 演算法是重複點增多
• 圖(c) 確定了 Tomek 線，用框表示
• 圖(d) 給出清理後的資料集

我們看出演算法過程更好地定義了類簇，這有助於提高分類效能。

實驗分析

為了說明不均衡資料集下對分類器演算法效能的影響，我們利用 UCI 資料集中的 german、haberman 進行分析，其中取 german 資料集中類 1 作為多數類，類 2 位少數類。SVM 演算法中 C=1000、核函式為高斯核、引數為 10、不均衡資料比取10:1，15:1，20:1，25:1，30:1，35:1，40:1，45:1

為了消除噪聲的影響，我們採用 10 次交叉驗證方法，每次驗證迴圈 20 次，取其平均結果，試驗中採用 RU 隨機欠抽樣，SMOTE 過抽樣，RU+SMOTE 演算法以及 BSMOTE 、ADASYN 過抽樣演算法進行分析比較。效能指標選擇 F-Measure ， G-Mean 和 AUC 。

從實驗結果不難看出，當 SVM 演算法面對這些不均衡資料集分類時，出現嚴重便宜使得少數類的效能為最低 (0)，因此導致 F-Measure ， G-Mean 和 AUC 的效能指標為 0。而其他基於資料預處理的不均衡資料分類方法均能有效提高演算法效能。最後，我們對這幾個演算法按照不均衡資料比例取其平均值，並將其結果進行對比。

最終總結出的結論是：針對不同的資料集分佈特徵，不同資料預處理方法的效能也大不相同，因此如何根據具體的資料分佈選擇合適的資料預處理方法是解決不均衡資料分類問題的關鍵。從結果中，我們還可以進一步看出，將兩種演算法進行有效地結合不失為一種解決該問題的好思路。