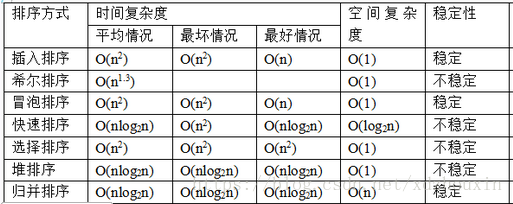
排序演算法之效能分析及總結
一、排序演算法說明
- 排序的定義:對一個無序的序列進行排序的過程。
輸入:n個數:a1,a2,a3,…,an。
輸出:n個數的排列:a1,a2,a3,…,an,使得a1<=a2<=a3<=…<=an。 - 排序的穩定性:相同值的節點相對位置是否會發生改變。
穩定:如果a原本在b前面,而a=b,排序之後a仍然在b的前面。
不穩定:如果a原本在b的前面,而a=b,排序之後a可能會出現在b的後面。 - 排序的時間複雜度:一個演算法執行所耗費的時間,一般在三種情況下考慮:最好情況、最壞情況、平均情況。
- 空間複雜度:執行完一個程式所需記憶體的大小。
二、各種排序演算法效能分析
1. 插入排序
1.1 直接插入排序
直接插入排序的原理是將未排好序的序列一個個地插入到已排好序的序列中,插入時,需要與已排好序的序列進行多次比較,直到找到合適的位置插入,而原來已排好序的部分節點可能需要進行後移操作,這個過程中需要一個額外的空間儲存一個值用於交換節點,所以空間複雜度為O(1)。
時間複雜度
最壞情況:當待排序序列正好為逆序狀態,首先遍歷整個序列,之後一個個地將待插入元素放在已排序的序列最前面,之後的所有元素都需要向後移動一位,所以比較和移動的時間複雜度都是O(n),再加上遍歷整個序列的複雜度,總複雜度為O(n^2)。
最好情況:當待排序序列正好為正序狀態,則遍歷完整個序列,當插入元素時,只比較一次就夠了,所以時間複雜度為O(n)。
平均情況:當被插入的元素放在已排序的序列中間位置時,為平均情況,比較和移動的時間複雜度為O(n/2),所以總的時間複雜度依然為O(n^2)。
穩定性
插入排序是在一個已經有序的小序列的基礎上,一次插入一個元素。當然,剛開始這個有序的小序列只有1個元素,就是第一個元素。比較是從有序序列的末尾開始,也就是想要插入的元素和已經有序的最大者開始比起,如果比它大則直接插入在其後面,否則一直往前找直到找到它該插入的位置。如果碰見一個和插入元素相等的,那麼插入元素把想插入的元素放在相等元素的後面。所以,相等元素的前後順序沒有改變,從原無序序列出去的順序就是排好序後的順序,所以插入排序是穩定的。
1.2 希爾排序
希爾排序是對直接插入排序的優化,它的原理是加大插入排序中元素的間隔,並在這些有間隔的元素中進行插入排序,從而使資料進行大幅度的移動,當進行過依次排序後,再減小間隔再一次進行插入排序,直到間隔縮小為1。這樣做的目的可以使得最後排序時整個序列基本有序,而無需再進行過多的元素比較和移動次數,在這個過程中也只需要一個額外的空間儲存一個值用於交換節點,所以空間複雜度
時間複雜度與增量的選取有關,計算起來較為複雜,不再細述。
穩定性
希爾排序是進行多次直接插入排序的演算法,由於多次插入排序,雖然每一次插入排序是穩定的,不會改變相同元素的相對順序,但在不同的插入排序過程中,相同的元素可能在各自的插入排序中移動,最後其穩定性就會被打亂,所以希爾排序是不穩定的。
2. 選擇排序
2.1 直接選擇排序
直接選擇排序的原理是在待排序的序列中選取最小(大)的值放在序列的第一個位置。遍歷整個序列,首先選取第一位置的值分別與之後所有的值比較,如果後邊值更小則與之交換,直到第一輪遍歷結束時,序列第一個位置的值就是最小的,接下來繼續從第二個、第三個做同樣的操作,此過程需要一個額外的空間儲存最小值用於交換,所以空間複雜度為O(1)。
時間複雜度
序列無論是正序還是逆序狀態,每一輪的最小值需要比較到最後才能確定,所以最壞情況和最好情況下都需要 比較n次,再加上遍歷整個序列的O(n),總的複雜度為O(n^2),平均情況的複雜度也是O(n^2)。
穩定性
直接選擇排序是給每個位置選擇當前元素最小的,比如給第一個位置選擇最小的,在剩餘元素裡面給第二個元素選擇第二小的,依次類推,直到第n-1個元素,第n個元素不用選擇了,因為只剩下它一個最大的元素了。那麼,在一趟選擇,如果當前元素比一個元素小,而該小的元素又出現在一個和當前元素相等的元素後面,那麼交換後穩定性就被破壞了。舉個例子,序列5 8 5 2 9, 第一遍選擇時第1個元素5會和2交換,那麼原序列中2個5的相對前後順序就被破壞了,所以選擇排序不是一個穩定的排序演算法。
2.2 堆排序
堆排序是對直接選擇排序的改進演算法,選擇排序的特點在於每次選取最小或最大的值,而選取最大值時的比較次數為複雜度的關鍵,堆排序採用二叉樹的方法儲存元素,每個節點都滿足父節點的值大於等於子節點的特點,與直接選擇排序類似,堆排序需要兩個個值的空間來儲存臨時變數,用於交換節點,一次用於儲存子樹最大節點用於交換子節點,一次用於儲存堆頂的值用於交換最後的節點,所以空間複雜度為O(1)。
採用堆的方式尋找最大值是降低時間複雜度的關鍵,假設有n個數據,需要n-1次建堆的過程,每次建堆的時間複雜度為log2n,但是無論序列的開始狀態如何,都需要對堆進行遍歷尋找最大值,所以在最好情況、最壞情況和平均情況下的時間複雜度都是O(nlog2n)。
穩定性
堆排序是利用堆的特點,堆的結構是節點i的孩子為2*i和2*i+1節點,大頂堆要求父節點大於等於其2個子節點,小頂堆要求父節點小於等於其2個子節點。在一個長為n 的序列,堆排序的過程是從第n/2開始和其子節點共3個值選擇最大(大頂堆)或者最小(小頂堆),這3個元素之間的選擇當然不會破壞穩定性。但當為n /2-1, n/2-2, …1這些個父節點選擇元素時,就會破壞穩定性。有可能第n/2個父節點交換把後面一個元素交換過去了,而第n/2-1個父節點把後面一個相同的元素沒有交換,那麼這2個相同的元素之間的穩定性就被破壞了。所以,堆排序不是一個穩定的排序演算法。
3. 交換排序
3.1 氣泡排序
氣泡排序是交換類排序演算法的典型實現,它的原理是遍歷整個序列,比較前後相鄰兩個值的大小,如果前邊比後邊大,則交換它們,直到序列的最後的兩個值進行比較,這樣最後的值就是最大的,之後再進行第二輪、第三輪遍歷,直到剩下序列的最前的值。從實現原理上可以知道,氣泡排序只需要一個值的空間用於交換節點,所以空間複雜度為O(1)。
時間複雜度
最壞情況:序列為逆序狀態,則每一輪遍歷都需要n次交換位置,所以時間複雜度為O(n^2)。
最好情況:序列為正序狀態,每一輪遍歷不需要交換位置,所以時間複雜度為O(n)。
平均情況:每一輪遍歷需要n/2次交換位置,所以時間複雜度依然為O(n^2)。
穩定性
氣泡排序就是把小的元素往前調或者把大的元素往後調。比較是相鄰的兩個元素比較,交換也發生在這兩個元素之間。所以,如果兩個元素相等,不會發生交換。如果兩個相等的元素沒有相鄰,那麼即使通過前面的兩兩交換把兩個相鄰起來,也不會發生交換,所以相同元素的前後順序並沒有改 變,所以氣泡排序是一種穩定排序演算法。
3.2 快速排序
快速排序是另一種交換類排序方法,它的原理是選擇一個基準元素,通常選擇第一個元素或者最後一個元素,通過一趟掃描,將待排序列分成兩部分,一部分比基準元素小,一部分大於等於基準元素,此時基準元素在其排好序後的正確位置,然後再用同樣的方法遞迴地排序劃分的兩部分。首先就地快速排序使用的空間是O(1)的,而真正消耗空間的就是遞迴呼叫了,因為每次遞迴就要保持一些資料,每一次都平分陣列的情況下空間複雜度為O(logn) ,最差的情況下空間複雜度為O(n)。
時間複雜度
最壞情況:每一次選取的基準元素都是最大或最小的,複雜度為O(n^2)
最好情況:每一次選取的基準元素都能平分整個序列,由於快排涉及到遞迴呼叫,所以時間複雜度為O(nlog2n)。
平均情況:平均情況下複雜度也是O(nlog2n)。
穩定性
快速排序有兩個方向,左邊的i下標一直往右走,當a[i]<=a[center_index],其中center_index是中樞元素的陣列下標,一般取為陣列第0個元素。而右邊的j下標一直往左走,當a[j]>a[center_index]。如果i和j都走不動了,i<=j, 交換a[i]和a[j],重複上面的過程,直到i>j。 交換a[j]和a[center_index],完成一趟快速排序。在中樞元素和a[j]交換的時候,很有可能把前面的元素的穩定性打亂,比如序列為 5 3 3 4 3 8 9 10 11,現在中樞元素5和3(第5個元素,下標從1開始計)交換就會把元素3的穩定性打亂,所以快速排序是一個不穩定的排序演算法,不穩定發生在中樞元素和a[j] 交換的時刻。
4. 歸併排序
歸併排序先遞迴的把陣列劃分為兩個子陣列,一直遞迴到陣列中只有一個元素,然後再呼叫函式把兩個子陣列排好序,因為該函式在遞迴劃分陣列時會被壓入棧,所以這個函式真正的作用是對兩個有序的子陣列進行排序。排序函式的步驟,讓兩個陣列的元素進行比較,把大的/小的元素存放到臨時陣列中,如果有一個數組的元素被取光了,那就直接把另一陣列的元素放到臨時陣列中,然後把臨時陣列中的元素都複製到實際的陣列中。所以 歸併的空間複雜度就是那個臨時的陣列和遞迴時壓入棧的資料佔用的空間n + logn,所以空間複雜度為:O(n)。
時間複雜度
歸併排序的時間主要花在了劃分序列和合並序列上,由於是採用遞迴的方式進行合併,所以與快速排序類似,樹的每層元元素的個數最多是n,也就代表著每層最多進行n次比較,而遞迴樹最多隻有log2n層,而且不管元素在什麼情況下都要做這些步驟,所以該演算法的最優時間複雜度和最差時間複雜度及平均時間複雜度都是一樣,都是O( nlogn )。
穩定性
歸併排序的原理是把序列遞迴地分成短序列,遞迴出口是短序列只有1個元素(認為直接有序)或者2個序列(1次比較和交換),然後把各個有序的段序列合併成一個有序的長序列,不斷合併直到原序列全部排好序。可以發現,在1個或2個元素時,1個元素不會交換,2個元素如果大小相等也不會交換,所以不會破壞穩定性。而在短的有序序列合併的過程中,穩定性也沒有受到破壞,合併過程中可以保證如果兩個當前元素相等時,把處在前面的序列的元素儲存在結果序列的前面,這樣就保證了穩定性。所以,歸併排序是穩定的排序演算法。