使用k-d樹進行無序點雲去噪
離散點雲的點之間是沒有拓撲結構的,因此為了找到它的幾何屬性,可以找到各點的鄰域結構。對於取樣點
那麼尋找K-nearest neighbours的方法主要由以下三種:
* 八叉樹法
* 空間網格法
* k-d樹法
一、八叉樹法
(1)首先確定資料點集最小包圍盒的邊長
(2)把點雲包圍盒平均分成8個小的包圍盒,對包含多個取樣點的包圍盒繼續分割,直到達到遞迴的終止條件,分割過程用八叉樹記錄;
(3)廣度遍歷八叉樹,利用資料點的空間分佈與包圍盒的空間關係,快速搜尋出任意取樣點
二、空間網格法
空間網格法也是基於對空間包圍盒的劃分,首先確定出包圍盒的大小
這樣不僅確定了空間結構,而且可以精化點雲資料。
三、k-d樹法
1、k-d樹的構建過程
下面以構建二維空間的k-d樹為例,介紹一種k-d樹的生成的方法。
(1)首先按
(2)對分隔好的空間按照
這樣的分割過程就對應於一個二叉樹,每個分割線對應於一個分支,每個點對應於一個葉子節點。
2、k-d樹的搜尋過程
假設這裡已經存在一棵已經建立好的二叉樹,如下圖所示:
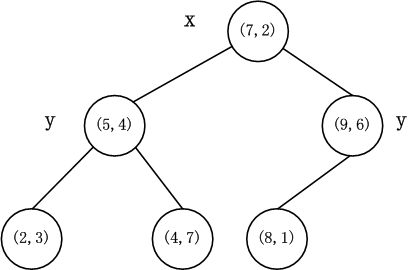
這是對一組二維點集
現在有一點
(1)首先在建立好的k-d樹上進行遍歷,因為
(2)計算
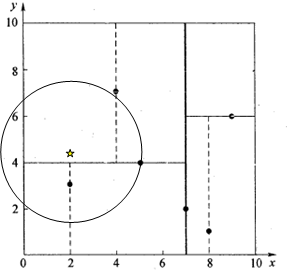
可見該圓與
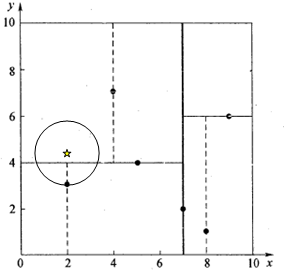
所以最終找的最近鄰點為
這裡有一個部落格對k-d樹的建立與查詢講得很詳細,我的例子就是參考的它的,感謝。
http://www.cnblogs.com/eyeszjwang/articles/2429382.html
四、根據k-d樹進行無序點雲去噪
(1)根據點雲資料生成k-d樹,建立點雲的拓撲關係;
(2)查詢任一點的的鄰域;
(3)計算該點與鄰域內各點的距離取平均值;
(4)判斷該平均值是否超過閾值,若超過則判定該點為噪點,進行去除。
