直觀來說,牛頓法因為使用了二階導資訊,比單純的一階導數的梯度下降法,其發現極值點回收斂得更快。

我個人的理解，梯度下降考慮了函式值下降最快的方向（梯度方向）。而在有些情況下，按這樣的規則改變自變數取值，可能會走彎路。

其根本原因在於，梯度下降法，能夠保證函式值在改點處的變化最快方向，但不能保證梯度本身向著最快變化方向變動。

大家經常見到的示意圖長這樣：

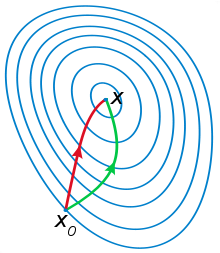
綠色的是梯度下降法，而紅色的是牛頓法。這張示意圖的目的就在於，說明牛頓法能夠向極值點收斂得更快。

梯度下降法，就好比從當前所在位置往負梯度方向走，能夠讓函式變小的速度最快，但是這個方向卻不一定是梯度本身往0變化最快的。

牛頓法的優勢便在於，能夠確保自變數取值變化的範圍向著梯度本身向0變化最快的方向

想象一下，上圖中的x0點處，綠線方向是坡度最大的方向，看起來往這個方向走能最快到達坑底。而紅線方向，雖然現在看起來前面只是一個緩坡，但實際上過了這個緩坡，前面就是一個大的懸崖。說白了就是，梯度無法給出除了x0點周圍一塊地方以外更遠處的資訊，而二階導卻可以。這裡不考慮懸崖可不可導和會不會摔死的問題……

當然了，更多的資訊也有更大的代價：牛頓法要計算二階導，這在高維資料時將非常耗費資源，額外資訊的獲取都是需要成本的。還有可能會碰到函式二階導數不存在的問題。針對於這兩個問題，擬牛頓法放鬆了假設，並以近似的方式取得二階導（Hessian矩陣），具體的我將在後面的文章中再給到。