NN這塊的公式，前饋網路是矩陣乘法。損失函式的定義也是一定的。

但是如何更新引數看了不少描述，下面的敘述比較易懂的：

1、在吳恩達的CS229的講義的第四頁直接給出引數迭代公式

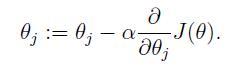
在UFLDL中反向傳導演算法一節也是直接給出的公式

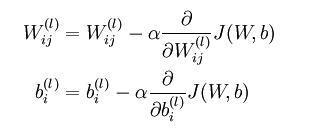
2、例子：

第一步：隨機對比重（a,b）賦值並計算誤差平方和（SSE）

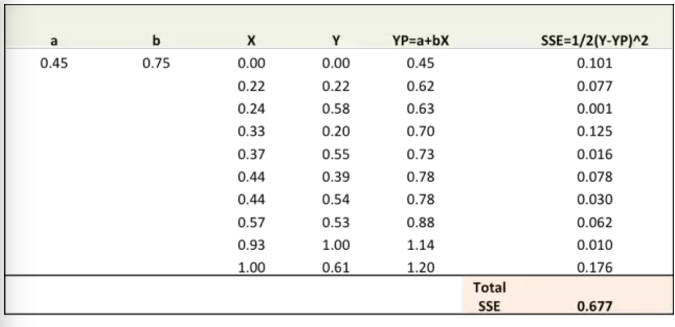
第二步：通過對誤差比重（a,b）求導計算出誤差梯度（注：YP即Ypred）

∂SSE/∂a = – (Y-YP)

∂SSE/∂b = – (Y-YP)X

誤差公式：SSE=½ (Y-YP)^2 = ½(Y-(a+bX))^2

這裡涉及到一些微積分，不過僅此而已。∂SSE/∂a 和 ∂SSE/∂b 就被稱之為梯度

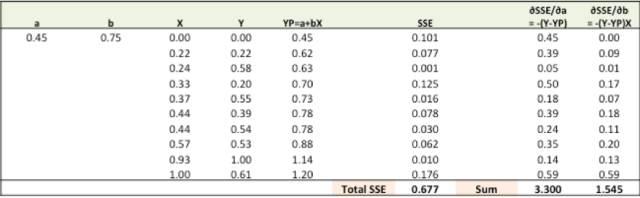
第三步：通過梯度調整a,b，使得a,b最佳即所得SSE最小

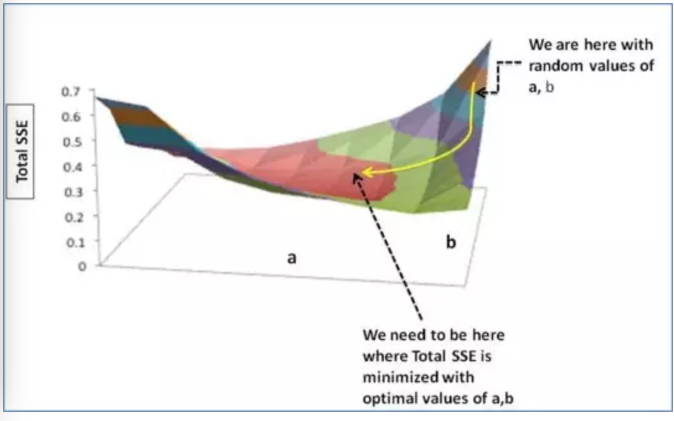
（右上角是我們隨機的a,b所取得的SSE值，我們需要找到圖中黑虛線所指的SSE最小值）

我們通過改變a,b來確保我們的SSE會向最小值方向移動，即沿黃線所指方向。至於改變a,b的規則：

• a – ∂SSE/∂a

• b – ∂SSE/∂b

所以，具體的公式就是：

• New a = a – r * ∂SSE/∂a = 0.45 - 0.01 * 3.300 = 0.42

• New b = b – r * ∂SSE/∂b = 0.75 - 0.01 * 1.545 = 0.73

在這裡，r代表學習率 = 0.01，可以自設，是用來決定調整a,b快慢的。越大調整的越快，但越容易漏掉收斂的最佳點。

第四步：用新的a,b來求出新的SSE

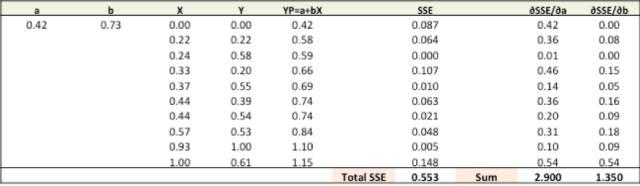
大家可以從圖上看出，總的SSE值（Total SSE）從原來的0.677變為0.553。代表著我們的預測準度正在增加。

第五步：重複三四步直到調整a,b不會明顯的影響SSE。到那時我們的預測準度就會達到最高

3、這就是梯度下降法，梯度更新公式不是推導而是創造然後定義出來的。

設想下有個函式，你的目標是：找到一個引數 使得它的值 最小。但它很複雜，你無法找到這個引數的解析解，所以你希望通過梯度下降法去猜這個引數。 問題是怎麼猜？

對於多數有連續性的函式來說，顯然不可能把每個 都試一遍。所以只能先隨機取一個 ，然後看看怎麼調整它最有可能使得

現在問題是怎麼調整？既然要調整，肯定是基於當前我們擁有的那個引數 ，所以有了：

那現在問題是每次更新的時候這個 應該取什麼值？

我們知道關於某變數的（偏）導數的概念是指當（僅僅）該變數往正向的變化量趨向於0時的其函式值變化量的極限。 所以現在若求 關於的導數，得到一個值比如:5,那就說明若現在我們把 往正向（即增大）一點點， 的值會變大，但不一定是正好+5。同理若現在導數是-5，那麼把 增大一點點 值會變小。 這裡我們發現不管導數值 是正的還是負的（正負即導數的方向），對於 來說， 的最終方向（即最終的正負號，決定是增（+）還是減（-））一定是能將Y值變小的方向（除非導數為0）。所以有了:

但是說到底， 的絕對值只是個關於Y的變化率，本質上和 沒關係。所以為了抹去 在幅度上對 的影響，需要一個學習率來控制： 。所以有了：

而這裡的 就是你1式中的那個偏導，而對於2式，就是有多少個引數，就有多少個不同的 。

現在分析在梯度下降法中最常聽到的一句話：“梯度下降法就是朝著梯度的反方向迭代地調整引數直到收斂。” 這裡的梯度就是 ,而梯度的反方向就是 的符號方向---梯度實際上是個向量。所以這個角度來說，即使我們只有一個引數需要調整，也可以認為它是個一維的向量。 整個過程你可以想象自己站在一個山坡上，準備走到山腳下（最小值的地方），於是很自然地你會考慮朝著哪個方向走，方向由 的方向給出，而至於一次走多遠，由 來控制。 這種方式相信你應該能理解其只能找到區域性最小值，而不是全域性的。

參考

1：作者：老董 連結：https://www.zhihu.com/question/57747902/answer/240695458 來源：知乎

2：https://zhuanlan.zhihu.com/p/27297638