1.前言

在講解梯度下降演算法時，經常可以看到下面這張圖(圖片來自Wiki百科):

這張圖後面一般都會再接一句，梯度下降的方向與等高線的切線方向垂直。
最開始的時候對這句話並沒有多想，覺得這理所應當。不過突然有一天回過神來，為什麼梯度下降方向與等高線的方向垂直啊？然後開始仔細考慮了一下這個問題。

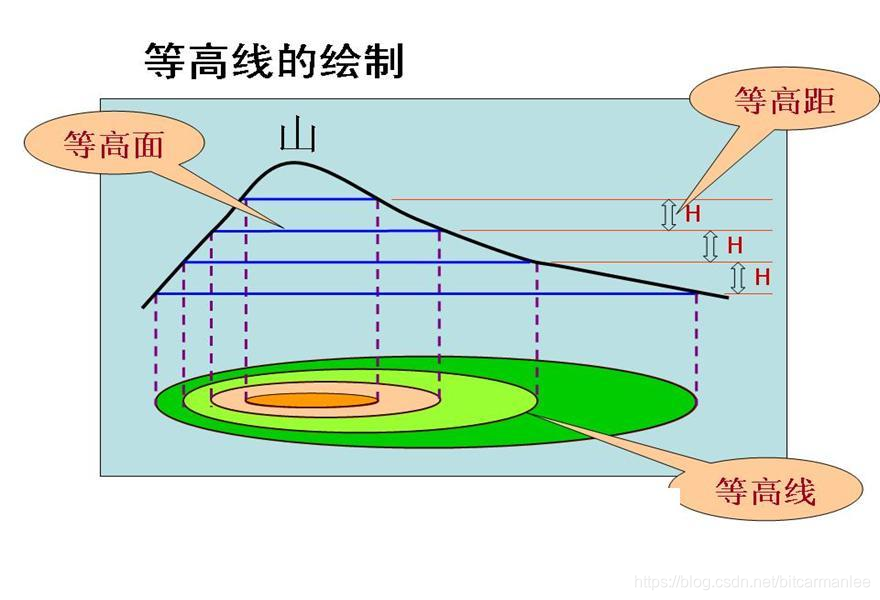
2.等高線

看到知乎上的一幅圖，能比較清楚地看出等高線的繪製過程，在此貼上過來。

3.梯度的定義

梯度的概念是為了解決這麼一個問題:
函式在變數空間(變數的維度可能很高)的某一點，沿著那個方向有最大的變化率？
梯度退化到xoy平面的二維空間，其實就是導數的概念。
梯度的定義如下:
$g$

需要注意如下幾點：
1.梯度是一個向量，既有大小又有方向。
2.梯度的方向是最大方向導數的方向。
3.梯度的模是方向導數的最大值。

4.梯度方向與等高線切線方向垂直

假設Loss Function為 $z = f(x,y)$，該函式為一個三維曲面。該面被平面 $z = c$所截的曲線方程為
$\begin{cases} z = f(x, y) \\ z = c \end{cases}$
該曲線在xoy平面上的投影是一條曲線，假設該曲線為Q，在xoy平面上該曲線的方程為
$f(x, y) = c$
不難看出，xoy平面上的曲線Q即為 $z = f(x, y)$的等高線。

等高線 $f(x, y) = c$上的任意一點p切線處的斜率為 $dy/dx$
而p點對應的法線的斜率則為:
$-\frac{1}{\frac{dy}{dx}} = -\frac{1}{-\frac{f_x}{f_y}} = \frac{f_y}{f_x}$
$\frac{dy}{dx} = -\frac{f_x}{f_y}$可以由隱函式求導公式推導得出。

而梯度的表示式為:
$\frac{\partial f}{\partial x}i + \frac{\partial f}{\partial y}j$
則梯度的方向為:
$\frac{\partial f}{\partial y} / \frac{\partial f}{\partial x} = \frac{f_y}{f_x}$

由此可見，梯度的方向與等高線切線的法向量方向是相同的！

參考文獻:
1.https://zhuanlan.zhihu.com/p/27731819