梯度彌散與梯度彌散
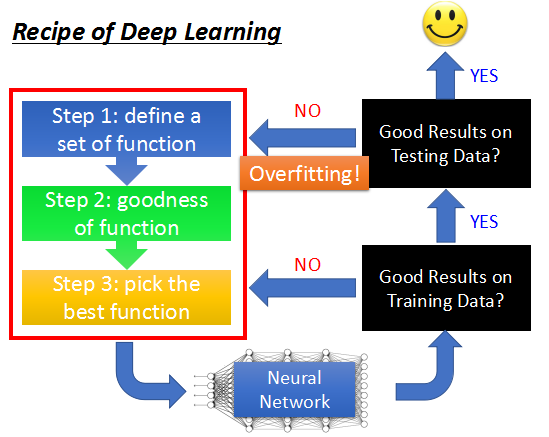
問題描述
先來看看問題描述。
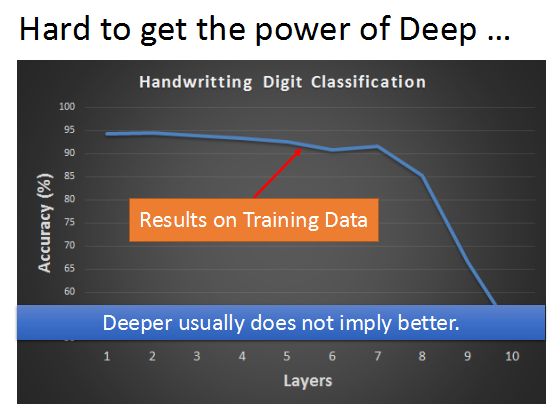
當我們使用sigmoid funciton 作為激活函數時，隨著神經網絡hidden layer層數的增加，訓練誤差反而加大了，如上圖所示。
下面以2層隱藏層神經網絡為例，進行說明。
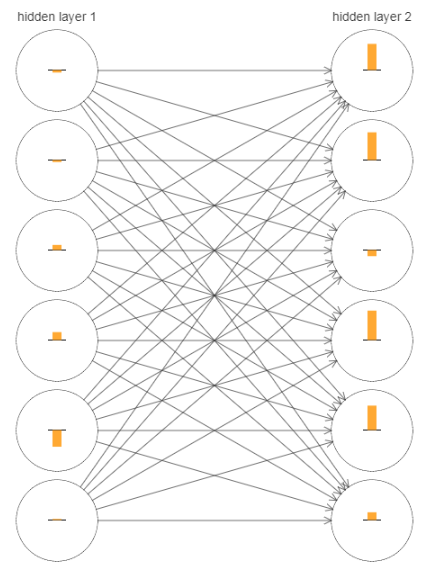
結點中的柱狀圖表示每個神經元參數的更新速率(梯度)大小，有圖中可以看出，layer2整體速度都要大於layer1.
我們又取每層layer中參數向量的長度來粗略的估計該層的更新速率，得到下圖。
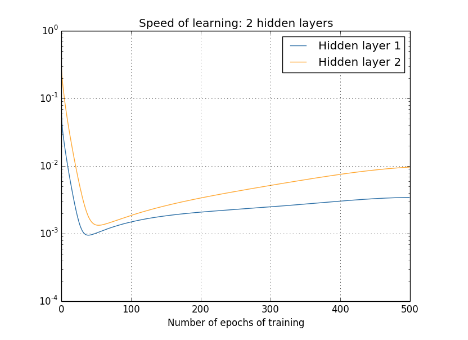
可以看出，layer2的速率都要大於layer1.
然後我們繼續加深神經網絡的層數。
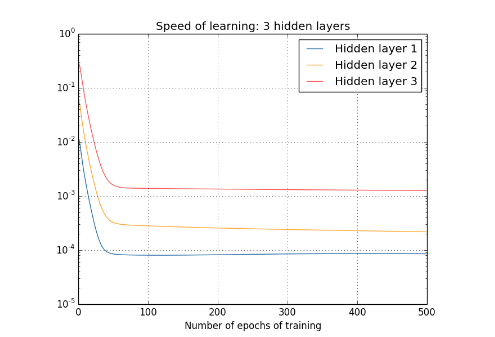
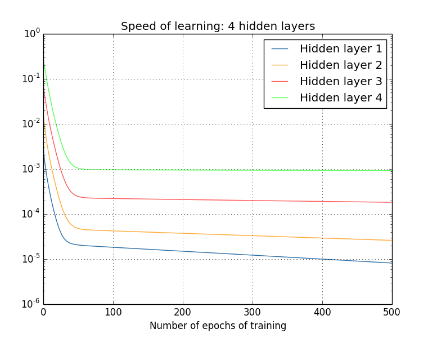
可以得到下面的結論：
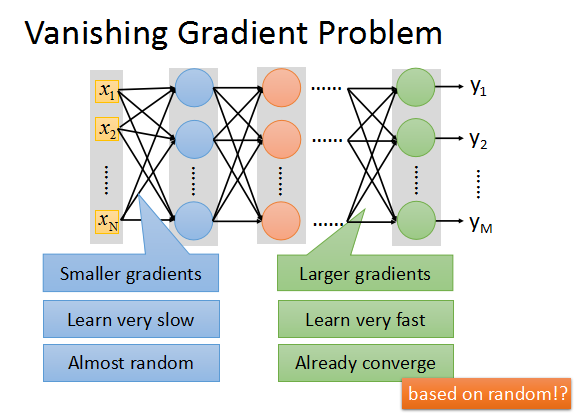
靠近輸出層的hidden layer 梯度大，參數更新快，所以很快就會收斂；
而靠近輸入層的hidden layer 梯度小，參數更新慢，幾乎就和初始狀態一樣，隨機分布。
在上面的四層隱藏層網絡結構中，第一層比第四層慢了接近100倍！！
這種現象就是梯度彌散（vanishing gradient problem）。而在另一種情況中，前面layer的梯度通過訓練變大，而後面layer的梯度指數級增大，這種現象又叫做梯度爆炸(exploding gradient problem)。
總的來說，就是在這個深度網絡中，梯度相當不穩定(unstable)。
直觀說明
那麽為何會出現這種情況呢？
現在我們來直觀的說明一下。
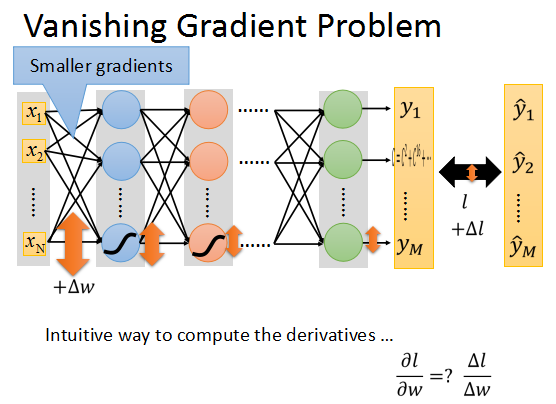
在上面的升級網絡中，我們隨意更新一個參數，加上一個Δw，(我們知道可以使用參數變化量來估計偏導數的大小)這個參數的更新會隨著網絡向前傳播。
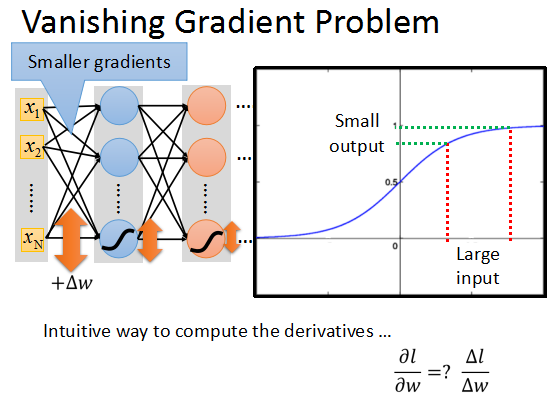
而根據sigmoid的特點，它會將+∞～-∞之間的輸入壓縮到0～1之間。當input的值更新時，output會有很小的更新。
又因為上一層的輸出將作為後一層的輸入，而輸出經過sigmoid後更新速率會逐步衰減，直到輸出層只會有微乎其微的更新。
數學說明
如果上面的例子還不夠清楚，下面我們來看看，不是很嚴密的數學證明。
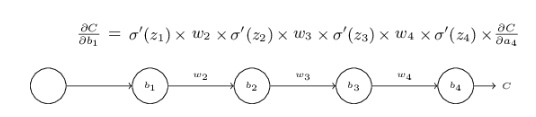
假設上面是一個三層hidden layer的神經網絡，每一層只有一個neuron，我們下面的分析僅僅針對bias，w也是可以類比的。
C是損失函數。
每一層的輸入為z，輸出為a，其中有z = w*a + b。
上面的等式?c/?b1由每一層的導數乘上對應的w最後乘上?c/?a4組成。
我們給b1一個小的改變Δb1，它會在神經網絡中起連鎖反應，影響最後的C。
我們使用變化率?c/?b1～Δc/Δb1來估計梯度。接下來可以進行遞推了。
先來計算Δb1對a1的影響。σ(z)為sigmoid函數。
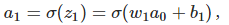
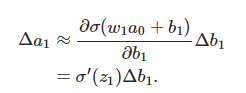
結果正好是上面?c/?b1等式的第一項，然後影響下一層的輸出。
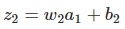
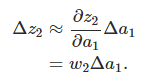
將上面推導出來的兩個式子聯合起來，就得到b1對於z2的影響：
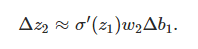
再和?c/?b1等式對比一下，驚喜！！
然後的推導就是完全一樣了，每個neuron的導數，乘上w，最終得到C的變化量：
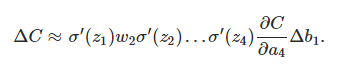
兩邊除以Δb1：
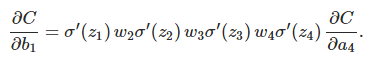
sigmoid導數圖像：
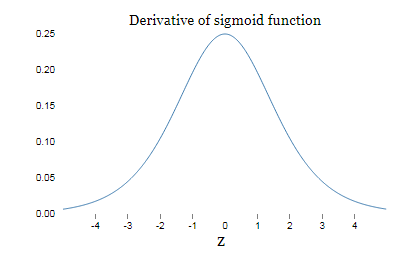
sigmoid導數在0取得最大值1/4。
如果我們使用均值為0，方差為1的高斯分布初始化參數w，有|w| < 1,所以有：
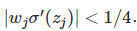
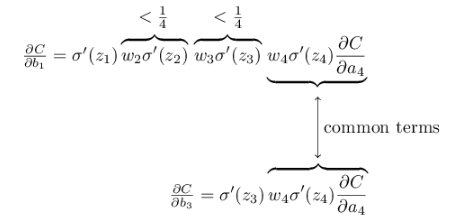
可以看出隨著網絡層數的加深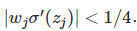的term也會變多，最後的乘積會指數級衰減，
這就是梯度彌散的根本原因。
而有人要問在train的時候如果參數w變得足夠大，就可能使|w|>1,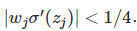就不滿足了。
的確這樣不會有梯度彌散問題，根據我們之前的分析，當|W|>1時，會使後面的layer參數指數級增加，從而引發梯度爆炸。
解決方法
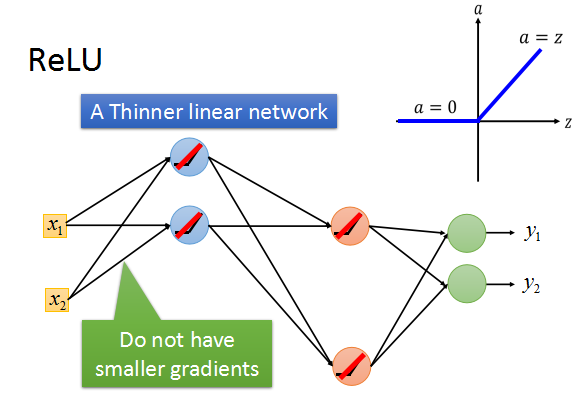
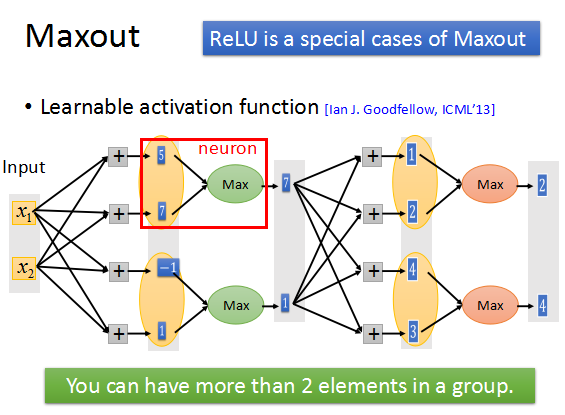
梯度不穩定的方法就是，使用其他激活函數替代sigmoid，比如Relu等等，這裏就不細說了。
參考文獻：http://neuralnetworksanddeeplearning.com/chap5.html#the_vanishing_gradient_problem
梯度彌散與梯度彌散