幾種最短路徑算的Python實現
最近學習了一些關於最短路徑演算法的知識,感覺很有意思,但是網路上很多的演算法鬥志又C或C++的實現方式,很少有Python。於是我就想來自己些個Python最短路徑的教程,權當複習自己的知識。
最短路徑演算法是圖類問題中一個經典問題,旨在尋找又節點和邊構成的圖中任意一點到任意一點的最短路徑。今天我要介紹的主要是Floyd-Warshall演算法,Dijkstra演算法和Bellman-Ford。演算法。
第一個介紹的是Floyd-Warshall演算法
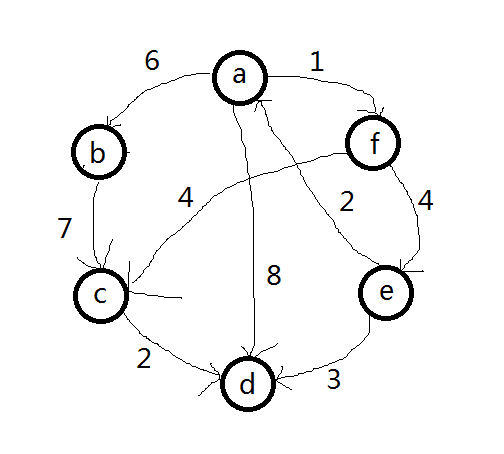
在這個圖中,字母表示頂點,數字表示每個定點之間的距離。假如我們現在要找出從A點到D點的的短路徑怎麼辦?你當然可以把每條路徑的距離都算出來,一一比較,像這樣。
A - D : 8
A - F - E - D : 8
A - B - C - D : 15
A - F - C - D : 7
最後發現最短的路徑是A - F - C - D,這個問題之所以能夠這樣解決,是因為我們的圖不復雜,可以使用窮舉的方法找出所有的可能。但是,如果說我們面對的是一個有500定點的圖,那我們要怎麼窮舉呢?這個時候我們就需要金光閃閃的Flolyd-Warshall演算法來幫助我們啦。
不過再具體學習演算法之前我們需要建立一個表格來儲存圖。X表示兩個點之間不能直接到達
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 6 | X | X | X | 1 |
| B | X | X | 7 | X | X | X |
| C | X | X | X | 2 | x | X |
| D | X | X | X | X | X | X |
| E | 2 | X | X | 3 | X | X |
| F | X | X | 4 | X | 4 | X |
得到這一個表格後,我們就可以很輕鬆的將這個錶轉換為二位陣列啦~
TaDa~現在真正要來介紹Floyd-Warshall演算法啦!其實Floyed演算法很簡單:
”如果說兩個點之間的直接路徑不是最短路徑的話,必然有一個或者多個點供中轉,使其路徑最短。“
那如何用計算機語言來描述這個演算法呢?
for i in range(len(vertex)):
for j in range(len 第一個迴圈和第二個迴圈的用途很明顯,用來定位二維陣列的值,按下不表。
第三個迴圈就是用來尋找供中轉的點了,需要特別注意,最開始學習這個演算法的時候我認為這個演算法只能找到一個點作為中轉,不能提供多個點供中轉,後面仔細一看發現我的理解是錯誤的。
現在假設我們有這樣一箇中轉方案
dis = [
[ 999 , 2, 999 , 999 , 2 , 10 ],
[ 999 , 999 , 999 , 999 , 999 , 6,],
[ 999 , 999 , 999 , 999 , 999 , 1 ],
[999 , 999 , 999 , 999 , 999 , 999 ],
[ 999, 999 ,1 ,999 , 999 , 999 ],
[ 999 ,999 ,999 , 999 , 999 ,999 ],
]
A - F : 10
A - B - F : 8
A - E - C - F : 6
我們可以直觀的發現1,從點A - 點F的最短距離是通過 E C 者兩個點近行中轉,那這個中轉在演算法中是如何實現的呢?
首先,計算機在找從A - C點的最短路徑時發現,[A][C]>[A][E]+[E][C]
著時,將A - C 的距離替換位 A - E -C ,這就意味著在後面所有由A點出發,C點中轉的點都變成從A點出發,經過E C兩個點轉。
然後計算機再找從A - F的,也會依次將 A - F之間所有的點都作為中轉點一一嘗試,但是在試到 A - C - F這個點時,由於 A - C的距離已經被更短的 A - E - C替換,友誼 A - C - F 實際上走的是 A - E - C - 這條路徑。
Floyd-Warshall演算法需要執行三次for迴圈,故其時間複雜度為O(N^3)。
Dijkstra 演算法
Floyd-Warshall演算法雖然好,但是每次計算都會將所有的的點之間的最短路徑計算出來,可是有的時候,我們也許只需要一個點到其他點之間的最短路徑,並不需要其他點之間的最短路徑。這時怎麼辦呢?Dijkstra 演算法這時就派上用場啦。
Dijkstra演算法 通過一種‘鬆弛’的思想來得出一個點到另一個點的最短路徑,具體怎麼算的呢,我們先來看一個例子,X表示距離無窮遠:
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 6 | X | 4 | X | 1 |
| B | 5 | X | 7 | 7 | X | X |
| C | X | X | X | 2 | 4 | X |
| D | X | 3 | 5 | X | 1 | 7 |
| E | 2 | X | X | 3 | X | X |
| F | X | 3 | 4 | X | 4 | X |
然後,我們新建一個列表來表示A點到其他點的距離
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 6 | X | 4 | X | 1 |
如果兩個部分的距離之和為最小值,那這兩個部分也應當為最小值,這就是Dijkstra 演算法的中心思想。觀察A 到其他點的距離,我們發現從A 點
到F點的直線距離最小,這時,我們稱從A 點 到 F點的這個距離為確定距離,然後使用F點來鬆弛其他的邊。
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | x | 5 | 1 |
這時我們發現,通過F點進行中轉可以有效的簡單,A - B, A - C,A - E的值,然後現仔,我們在從A 到 除 F而外的所有點中,找出距離最小的點,最為確定值,進行下一一次鬆弛。 然後我們發現,A - B 點的距離目前最短,所以再用B點進行一次鬆弛。
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | 11 | 5 | 1 |
現在我們得到了由B點進行鬆弛過後的結果,現在再來繼續尋找除 B,F意外距離A點最近的點,然後我們發現C 點和E 點都是5,那我們就現在用C點進行鬆弛
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | 7 | 5 | 1 |
然後我們發現 經過 C點鬆弛, A - D的距離可以變短,現在,我們是用E點進行鬆弛
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | 7 | 5 | 1 |
沒有什麼變化,現在在使用最後的D點進行鬆弛,由於D點是最後一個點,一般來說當使用最後一個點進行鬆弛時,最短路徑其實已經找了出來。所以A 到其他各個定點的最短路徑為
| \ | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | X | 4 | 5 | 7 | 5 | 1 |
那現在,這個演算法要怎麼使用Python描述出來呢?
nodes = ('A', 'B', 'C', 'D', 'E', 'F', 'G')
distances = {
'B': {'A': 5, 'D': 1, 'G': 2},
'A': {'B': 5, 'D': 3, 'E': 12, 'F' :5},
'D': {'B': 1, 'G': 1, 'E': 1, 'A': 3},
'G': {'B': 2, 'D': 1, 'C': 2},
'C': {'G': 2, 'E': 1, 'F': 16},
'E': {'A': 12, 'D': 1, 'C': 1, 'F': 2},
'F': {'A': 5, 'E': 2, 'C': 16}}
unvisited = {node: None for node in nodes} #把None作為無窮大使用
visited = {}#用來記錄已經鬆弛過的陣列
current = 'B' #要找B點到其他點的距離
currentDistance = 0
unvisited[current] = currentDistance#B到B的距離記為0
while True:
for neighbour, distance in distances[current].items():
if neighbour not in unvisited: continue#被訪問過了,跳出本次迴圈
newDistance = currentDistance + distance#新的距離
if unvisited[neighbour] is None or unvisited[neighbour] > newDistance:#如果兩個點之間的距離之前是無窮大或者新距離小於原來的距離
unvisited[neighbour] = newDistance#更新距離
visited[current] = currentDistance#這個點已經鬆弛過,記錄
del unvisited[current]#從未訪問過的字典中將這個點刪除
if not unvisited: break#如果所有點都鬆弛過,跳出此次迴圈
candidates = [node for node in unvisited.items() if node[1]]#找出目前還有拿些點未鬆弛過
current, currentDistance = sorted(candidates, key = lambda x: x[1])[0]#找出目前可以用來鬆弛的點
這段程式碼的第一次迴圈不會用任何點進行鬆弛,第一次迴圈的主要目的在於將目前到各個點的距離排個序,找出下一次用來鬆弛的點。這個演算法的時間複雜度只有O(N^2)。如果具備堆的知識,還可以順利的把這個演算法的時間複雜度降到O(M+N)LogN。但是,這回演算法依然不能解決帶負權的圖,那我們遇到帶負權的圖又該怎麼辦呢?這時我們就需要Bellman-Ford演算法啦!
Bellman-Ford演算法
Bellman-Ford演算法可以非常好的解決帶有負權的最短路徑問題,什麼是負權?如果兩個頂點之間的距離為正數,那這個距離成為正權。反之,如果一個頂點到一個頂點的距離為負數,那這個距離就稱為負權。Bellman-Ford和Dijkstra 相似,都是採用‘鬆弛’的方法來尋找最短的距離。現在,我們來看看Bellman-Ford的例子。
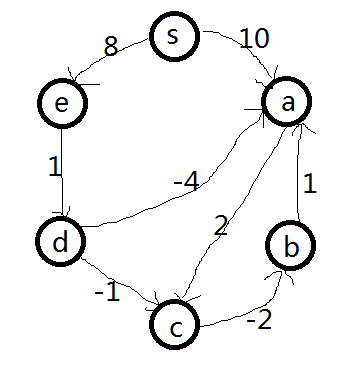
Bellman-Ford是如何找到從S點到其他點的最短距離的呢?
初始狀態:
| s: | a: | b: | c: | d: | e: |
|---|
第一次鬆弛我們發現,S點可以直接到達e點和a點,然後通過e點和a點可以到達d,c,,然後通過c點可以到達b,現在更新我們的表格
| s: | a:10 | b:10 | c:12 | d:9 | e:8 |
|---|
當所有點都鬆弛過一次後,我們進行第二次鬆弛,在進行第二次鬆弛的時候,我會可以發現d到啊a,c都是負權,應該可以減少距離。
| s: | a:5 | b:10 | c:8 | d:9 | e:8 |
|---|
這時第二次鬆弛的結果,現在我們要進行第三次次鬆弛
| s: | a:5 | b:5 | c:7 | d:9 | e:8 |
|---|
好了現在我們要開始第四次鬆弛了,所以到底我們需要幾次鬆弛呢。請偶們需要頂點數減一次鬆弛,因為在圖中,任意兩點的最短路徑至多包含N-1條邊,如果經過N-1次鬆弛以後還能繼續鬆弛,則說明這個圖是一個有負權迴路的圖,沒有最短路徑。
第四次鬆弛:
| s: | a:5 | b:5 | c:7 | d:9 | e:8 |
|---|
第四次鬆弛與第三次鬆弛結果一直,這說明我們現在已經找到從S點到圖中其他的最短路徑。
關門!上程式碼!
G = {1:{1:0, 2:-3, 5:5},
2:{2:0, 3:2},
3:{3:0, 4:3},
4:{4:0, 5:2},
5:{5:0}}
def getEdges(G):
""" 讀入圖G,返回其邊與端點的列表 """
v1 = [] # 出發點
v2 = [] # 對應的相鄰到達點
w = [] # 頂點v1到頂點v2的邊的權值
for i in G:
for j in G[i]:
if G[i][j] != 0:
w.append(G[i][j])
v1.append(i)
v2.append(j)
return v1,v2,w
def Bellman_Ford(G, v0, INF=999):
v1,v2,w = getEdges(G)
# 初始化源點與所有點之間的最短距離
dis = dict((k,INF) for k in G.keys())
dis[v0] = 0
# 核心演算法
for k in range(len(G)-1): # 迴圈 n-1輪
check = 0 # 用於標記本輪鬆弛中dis是否發生更新
for i in range(len(w)): # 對每條邊進行一次鬆弛操作
if dis[v1[i]] + w[i] < dis[v2[i]]:
dis[v2[i]] = dis[v1[i]] + w[i]
check = 1
if check == 0: break
# 檢測負權迴路
# 如果在 n-1 次鬆弛之後,最短路徑依然發生變化,則該圖必然存在負權迴路
flag = 0
for i in range(len(w)): # 對每條邊再嘗試進行一次鬆弛操作
if dis[v1[i]] + w[i] < dis[v2[i]]:
flag = 1
break
if flag == 1:
# raise CycleError()
return False
return dis
v0 = 1
dis = Bellman_Ford(G, v0)
print dis.values()Bellman-Ford演算法的時間複雜度是O(MN),但是我們依然可以對這個演算法進行優化,在實際使用中,我們常常會發現不用迴圈到N-1次就能求出最短路徑,所以我們可以比較前後兩次鬆弛結果,若果兩次結果都一致,可說明鬆弛完成,不用再繼續迴圈了。
Bellman-Ford與Dijkstra的區別
Bellman-Ford可以用於含有負權的圖中而Dijkstra不可以。
為什麼Dijkstra不可以?其跟本的原因在於,在Dijkstra,一旦一個頂點用來鬆弛過以後,其最小值已經固定不會再參與到下一次的鬆弛中。因為Dijkstra中全部的距離都是正權,所以不可能出現A - B - C 之間的距離比 A - B - D - C 的距離短的情況,而Bellman-Ford則在每次迴圈中,則會將每個點都重新鬆弛一遍,所以可以處理負權。
暫時就想到這一點的區別,想起來再補充咯,啾咪~
