最近在看斯坦福大學的機器學習的公開課，學習了支援向量機，再結合網上各位大神的學習經驗總結了自己的一些關於支援向量機知識。

一、什麼是支援向量機(SVM)?

1、支援向量機（Support Vector Machine，常簡稱為SVM）是一種監督式學習的方法，可廣泛地應用於統計分類以及迴歸分析。支援向量機屬於一般化線性分類器，這族分類器的特點是他們能夠同時最小化經驗誤差與最大化幾何邊緣區，因此支援向量機也被稱為最大邊緣區分類器。

2、支援向量機將向量對映到一個更高維的空間裡，在這個空間裡建立有一個最大間隔超平面。在分開資料的超平面的兩邊建有兩個互相平行的超平面，分隔超平面使兩個平行超平面的距離最大化。假定平行超平面間的距離或差距越大，分類器的總誤差越小。

3、假設給定一些分屬於兩類的2維點，這些點可以通過直線分割， 我們要找到一條最優的分割線，如何來界定一個超平面是不是最優的呢?

如下圖：

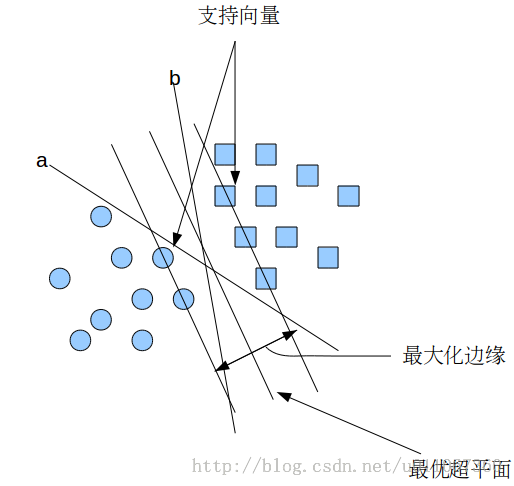
在上面的圖中，a和b都可以作為分類超平面，但最優超平面只有一個，最優分類平面使間隔最大化。 那是不是某條直線比其他的更加合適呢? 我們可以憑直覺來定義一條評價直線好壞的標準:

距離樣本太近的直線不是最優的，因為這樣的直線對噪聲敏感度高，泛化性較差。 因此我們的目標是找到一條直線（圖中的最優超平面），離所有點的距離最遠。 由此， SVM演算法的實質是找出一個能夠將某個值最大化的超平面，這個值就是超平面離所有訓練樣本的最小距離。這個最小距離用SVM術語來說叫做間隔(margin) 。

二、如何計算最優超平面?

1、線性分類：

我們通常希望分類的過程是一個機器學習的過程。這些資料點並不需要是中的點，而可以是任意的點（一個超平面，在二維空間中的例子就是一條直線）。我們希望能夠把這些點通過一個n-1維的超平面分開，通常這個被稱為線性分類器。有很多分類器都符合這個要求，但是我們還希望找到分類最佳的平面，即使得屬於兩個不同類的資料點間隔最大的那個面，該面亦稱為最大間隔超平面。如果我們能夠找到這個面，那麼這個分類器就稱為最大間隔分類器。

我們從下面一個圖開始：

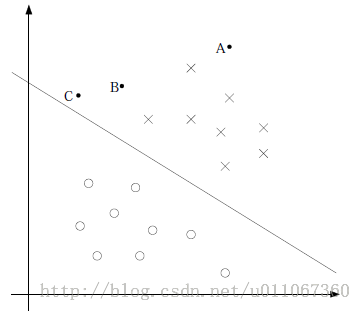
中間那條線是wx + b =0，我們強調所有點儘可能地遠離中間那條線。考慮上面3個點A、B和C。從圖中我們可以確定A是×類別的，然而C我們是不太確定的，B還算能夠確定。這樣我們可以得出結論，我們更應該關心靠近中間分割線的點，讓他們儘可能地遠離中間線，而不是在所有點上達到最優。因為那樣的話，要使得一部分點靠近中間線來換取另外一部分點更加遠離中間線。同時這個所謂的超平面的的確把這兩種不同形狀的資料點分隔開來，在超平面一邊的資料點所對應的 y 全是 -1 ，而在另一邊全是 1 。

我們可以令分類函式：

顯然，如果 f(x)=0 ，那麼 x 是位於超平面上的點。我們不妨要求對於所有滿足 f(x)<0 的點，其對應的="" y="" 等於="" -1="" ，而="" f(x)="">0 則對應 y=1 的資料點。如下圖。

最優超平面可以有無數種表達方式，即通過任意的縮放 w 和 b 。 習慣上我們使用以下方式來表達最優超平面

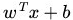 =1

式中 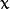 表示離超平面最近的那些點，也可以就可以得到支援向量的表示式為：y(wx + b) = 1，

上面說了，我們令兩類的點分別為+1, -1，所以當有一個新的點x需要預測屬於哪個分類的時候，我們用sgn(f(x))，就可以預測了，sgn表示符號函式，當f(x) > 0的時候，sgn(f(x)) = +1, 當f(x) < 0的時候sgn(f(x)) = –1。

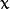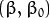通過幾何學的知識，我們知道點  到超平面  的距離為:

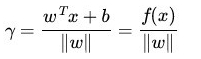
特別的，對於超平面, 表示式中的分子為1，因此支援向量到超平面的距離是

||w||的意思是w的二範數。

剛才我們介紹了間隔(margin),這裡表示為 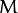, 它的取值是最近距離的2倍:

M = 2 / ||w||

最大化這個式子等價於最小化||w||, 另外由於||w||是一個單調函式，我們可以對其加入平方，和前面的係數，熟悉的同學應該很容易就看出來了，這個式子是為了方便求導。

最後最大化 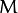 轉化為在附加限制條件下最小化函式：

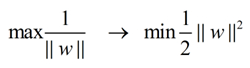
即：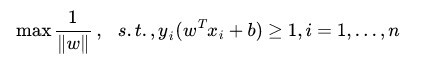

這是一個拉格朗日優化問題，可以通過拉格朗日乘數法得到最優超平面的權重向量W和偏置 b 。

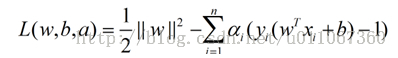
PS

1、咱們就要確定上述分類函式f(x) = w.x + b（w.x表示w與x的內積）中的兩個引數w和b，通俗理解的話w是法向量，b是截距;

2、那如何確定w和b呢？答案是尋找兩條邊界端或極端劃分直線中間的最大間隔（之所以要尋最大間隔是為了能更好的劃分不同類的點，下文你將看到：為尋最大間隔，匯出1/2||w||^2，繼而引入拉格朗日函式和對偶變數a，化為對單一因數對偶變數a的求解，當然，這是後話），從而確定最終的最大間隔分類超平面hyper plane和分類函式；

3、進而把尋求分類函式f(x) = w.x + b的問題轉化為對w，b的最優化問題，最終化為對偶因子的求解。