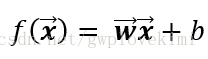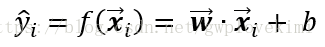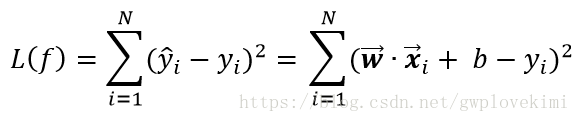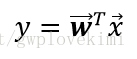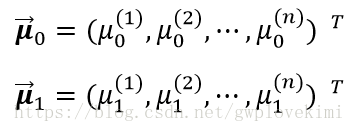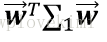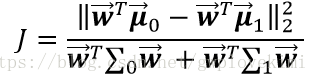本博文主要參考書籍為：

• 《Python大戰機器學習》

Fisher分類器也叫Fisher線性判別（Fisher Linear Discriminant），或稱為線性判別分析（Linear Discriminant Analysis，LDA）。LDA有時也被稱為Fisher's LDA。最初於1936年，提出Fisher線性判別，後來於1948年，進行改進成如今所說的LDA。

線性模型

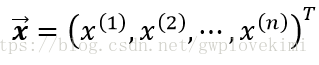
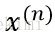
對於給定樣本，其中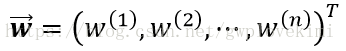為樣本的第n種特徵。線性模型的形式為：

其中，為每個特徵對應的權重生成的權重向量。其實這個線性模型也就類似於學習筆記（3）中的sigmoid函式的輸入。當然啦，邏輯斯蒂迴歸也是線性模型之一。

線性模型的物理表示：二維空間就是一條直線，三維空間就是一個平面，推廣到n維空間~

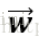
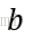
常見的線性模型有：嶺迴歸、lasso迴歸、邏輯斯蒂迴歸以及Fisher等。正如在上一節筆記中所言，邏輯斯蒂迴歸分類器構建的過程正是通過訓練資料來獲得一系列的權重向量。在此處則是拓展為：根據訓練資料集來計算引數和。

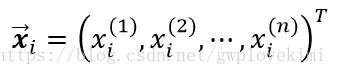
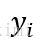
對於具有N個訓練樣本的樣本集，每個給定的樣本（注意，這裡是N個訓練樣本，每個訓練樣本有n個特徵。而樣本集中，訓練樣本的標籤為，而預測值為：

則模型的損失函式為：

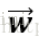
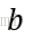
通過使損失函式最小化，即可以獲得要求的引數和；通過梯度下降或者梯度上升演算法（最優化演算法）可以求解。

關於特徵歸一化的意義：

特徵歸一化有兩個意義，1、提升模型的收斂速度；2、提升模型的精度。詳細分析見下面圖片：

LDA或Fisher：

Fisher的基本思想是：

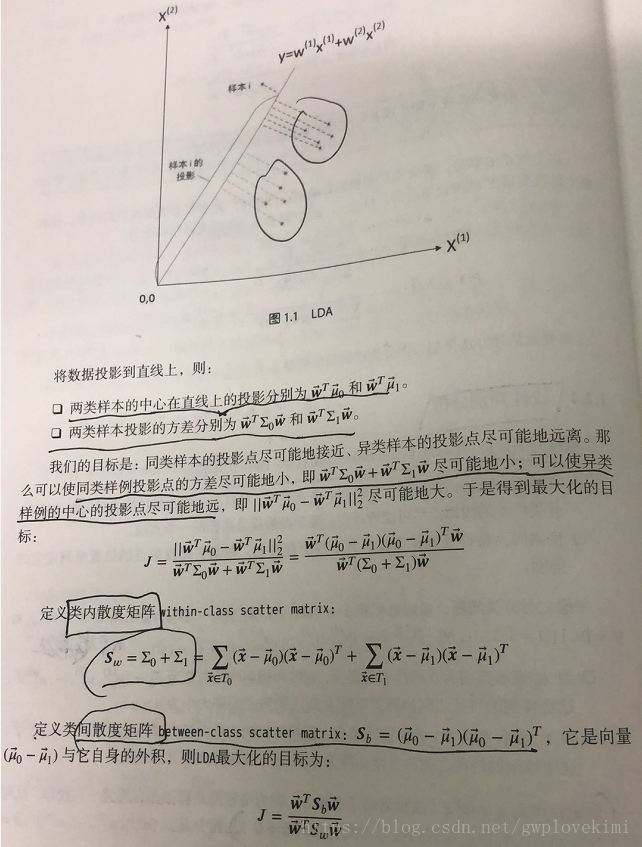
訓練時，將訓練樣本投影到某條直線上，這條直線可以使得同類型的樣本的投影點儘可能接近，而異型別的樣本的投影點儘可能遠離。要學習的就是這樣的一條直線。

預測時，將待預測資料投影到上面學習到的直線上，根據投影點的位置來判斷所屬於的類別。

下面直接給出書上關於LDA的推導過程的照片：

下面結合本人的理解，對推導過程做簡單的分析：

將樣本投影到直線上，假設直線為

對於標籤為0類和1類樣本，其特徵值的均值為向量（每個樣本有多個特徵值，每種特徵值的均值組成一個向量）：

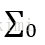
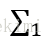
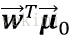
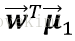
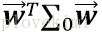
對應的樣例之間的協方差矩陣為和。那麼兩類樣本的中心在直線上的投影分別為和，而兩類樣本的投影的方差分別為：和

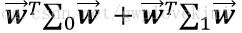
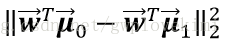
由於Fisher的準則是：同類型的投影點儘可能近，也即是，兩類樣本的投影方差都儘可能小，那麼他們之和也儘可能小，即儘可能小。而異型別的投影點儘可能遠，也就是異型別投影點的中心儘可能遠，也就是儘可能的大。那麼就可以獲得目標函式為：

通過使這個目標函式儘可能的大，就可以滿足Fisher判別準則。通過朗格朗日乘子法則可以解決這一最優化的問題。至於其具體的推導過程以及上面書本中的類內離散度矩陣和類間離散度矩陣這些就不一一展開了~個人感覺上面文字描述這部分理解了，Fisher就算大概明白了。scikit-learn中也有LDA的函式，下面給出測試程式碼~

給出Python程式碼如下：

from sklearn import datasets, cross_validation,discriminant_analysis

###############################################################################
#用鶯尾花資料集
def load_data():
    iris=datasets.load_iris()
    return cross_validation.train_test_split(iris.data,iris.target,test_size=0.25,random_state=0,stratify=iris.target)  
    #返回為: 一個元組，依次為：訓練樣本集、測試樣本集、訓練樣本的標記、測試樣本的標記 
    
###############################################################################
def test_LinearDiscriminantAnalysis(*data):
    x_train,x_test,y_train,y_test=data
    lda=discriminant_analysis.LinearDiscriminantAnalysis()
    lda.fit(x_train,y_train)
    print('Coefficients:%s, intercept %s'%(lda.coef_,lda.intercept_))#輸出權重向量和b
    print('Score: %.2f' % lda.score(x_test, y_test))#測試集
    print('Score: %.2f' % lda.score(x_train, y_train))#訓練集

###############################################################################
x_train,x_test,y_train,y_test=load_data()
test_LinearDiscriminantAnalysis(x_train,x_test,y_train,y_test)

結果如下圖所示：

在測試集上預測準確率為100%，而在訓練集上預測準確率為97%。

Fisher的這種對映關係還有一種作用就是作為降維技術，稱為監督降維技術（因為是有訓練資料的，所以稱為監督）

下面來看看原始的資料集經過Fisher投影后的資料集的情況。

from sklearn import datasets, cross_validation,discriminant_analysis

###############################################################################
#用鶯尾花資料集
def load_data():
    iris=datasets.load_iris()
    return cross_validation.train_test_split(iris.data,iris.target,test_size=0.25,random_state=0,stratify=iris.target)  
    #返回為: 一個元組，依次為：訓練樣本集、測試樣本集、訓練樣本的標記、測試樣本的標記 
    

###############################################################################
def plot_LDA(converted_X,y):
    '''
    繪製經過 LDA 轉換後的資料

    :param converted_X: 經過 LDA轉換後的樣本集
    :param y: 樣本集的標記
    :return:  None
    '''
    from mpl_toolkits.mplot3d import Axes3D
    import matplotlib.pyplot as plt 
    fig=plt.figure()
    ax=Axes3D(fig)
    colors='rgb'
    markers='o*s'
    for target,color,marker in zip([0,1,2],colors,markers):
        pos=(y==target).ravel()
        X=converted_X[pos,:]
        ax.scatter(X[:,0], X[:,1], X[:,2],color=color,marker=marker,
			label="Label %d"%target)
    ax.legend(loc="best")
    fig.suptitle("Iris After LDA")
    plt.show()
    

###############################################################################
import numpy as np
x_train,x_test,y_train,y_test=load_data()
X=np.vstack((x_train,x_test))#沿著豎直方向將矩陣堆疊起來，把訓練與測試的資料放一起來看
Y=np.vstack((y_train.reshape(y_train.size,1),y_test.reshape(y_test.size,1)))#沿著豎直方向將矩陣堆疊起來
lda = discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(X, Y)
converted_X=np.dot(X,np.transpose(lda.coef_))+lda.intercept_
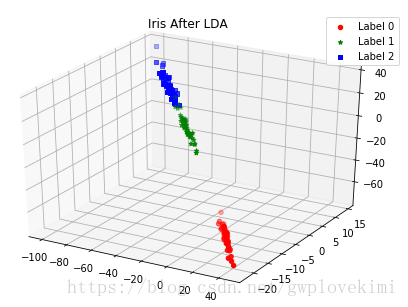
plot_LDA(converted_X,Y)

結果如下圖所示：

可以看出，Fisher確實能夠實現降維。假設存在M個類，則多分類LDA可以將樣本投影到M-1維空間。

好~關於Fisher分類器的學習筆記告一段落，後續有新的體會會及時更新，歡迎廣大讀者朋友賜教

補充：

通過線性判別分析壓縮無監督資料

LDA是一種可作為特徵抽取的技術，它可以提高資料分析過程中的計算效率，同時，對於不適用於正則化的模型，它可以降低因維度災難帶來的過擬合。

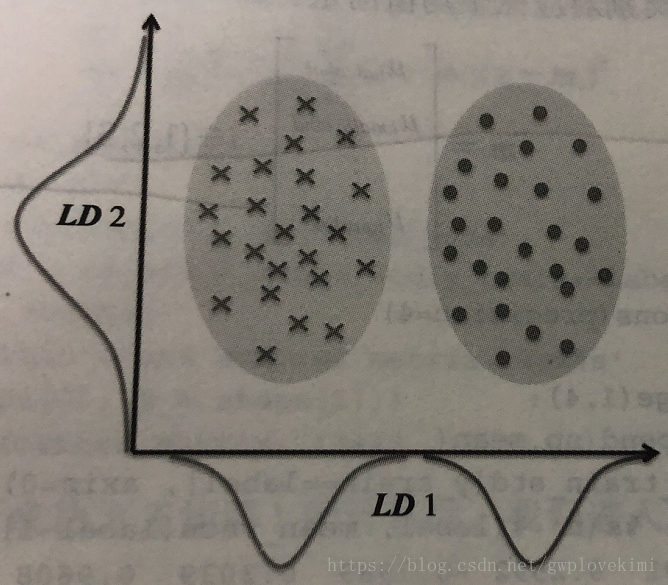
LDA的基本概念與PCA非常相似（見博文機器學習筆記6）。PCA試圖在資料集中找到方差最大的正交的主成分分量的軸，而LDA的目標是發現可以最優化分類的特徵子空間。其中，PCA是無監督演算法，而LDA是監督演算法，因此，直觀上，LDA比PCA更優越。如下圖所示：

如圖所示，在x軸方向（LD1），通過線性判定，可以很好地將呈正態分佈的兩個類分開。雖然沿y軸（LD2）方向的線性判定保持了資料集較大方差，但是沿此方向無法提供關於類別區分的任何資訊，因此它不是一個好的線性判定。一個關於LDA的假設是：資料呈正態分佈。此外，還假設各類別中資料具有相同的協方差矩陣，且樣本的特徵從統計上來講是相互獨立的。不過即使一個或多個假設沒有滿足，LDA仍舊可以很好的完成降維工作。

給出LDA資料降維和邏輯斯蒂迴歸分類的Python程式碼如下：

#####################################定義一個畫圖函式###########################
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

def plot_decision_regions(X, y, classifier, resolution=0.02):

    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    # plot class samples
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], 
                    y=X[y == cl, 1],
                    alpha=0.6, 
                    c=cmap(idx),
                    edgecolor='black',
                    marker=markers[idx], 
                    label=cl)


##############################資料的讀入、劃分、標準化###########################
import pandas as pd
#Python Data Analysis Library 或 pandas 是基於NumPy 的一種工具，該工具是為了解決資料分析任務而建立的。
#Pandas 納入了大量庫和一些標準的資料模型，提供了高效地操作大型資料集所需的工具。
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)
#讀入csv檔案，形成一個數據框
#使用葡萄酒資料集


from sklearn.cross_validation import train_test_split
x, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
x_train, x_test, y_train, y_test =train_test_split(x, y, test_size=0.3,stratify=y,random_state=0)
#葡萄酒資料集劃分為訓練集和測試集，分別佔據資料集的70%和30%

#使用單位方差對資料集進行標準化
from sklearn.preprocessing import StandardScaler
sc=StandardScaler()
#注意，當改為from sklearn.preprocessing import StandardScaler as sc時，會報錯
# fit_transform() missing 1 required positional argument: 'X'。這就是由於sc沒有StandardScaler()而僅僅是StandardScaler
x_train_std=sc.fit_transform(x_train)
x_test_std=sc.fit_transform(x_test)


#####################################使用sklearn中的LDA類#######################
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)#選取兩個主成分
#做降維處理
x_train_lda = lda.fit_transform(x_train_std, y_train)
x_test_lda=lda.transform(x_test_std)

#用邏輯斯蒂迴歸進行分類(對訓練資料進行處理)
lr=LogisticRegression()
lr.fit(x_train_lda,y_train)
plot_decision_regions(x_train_lda,y_train,classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

#用邏輯斯蒂迴歸進行分類(對測試資料進行處理)
lr=LogisticRegression()
lr.fit(x_train_lda,y_train)
plot_decision_regions(x_test_lda,y_test,classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
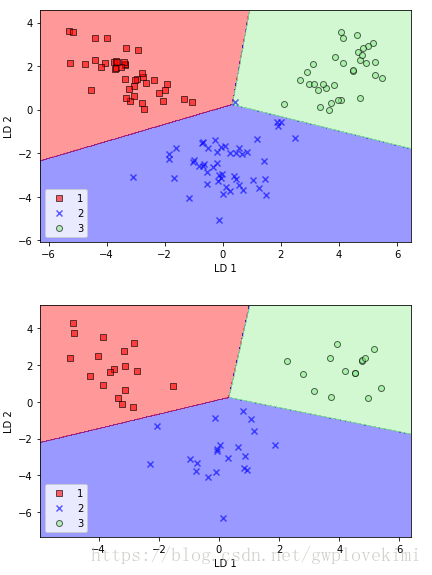
plt.show()

結果如圖所示：

可與機器學習筆記（6）中的PCA做一下對比~

此部分主要參考書籍為：

• 《Python機器學習》