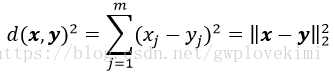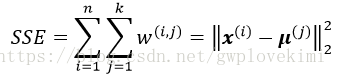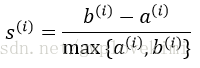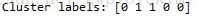對於監督學習，訓練資料都是事先已知預測結果的，即訓練資料中已提供了資料的類標。無監督學習則是在事先不知道正確結果（即無類標資訊或預期輸出值）的情況下，發現數據本身所蘊含的結構等資訊。

無監督學習通過對無標記訓練樣本的學習來尋找這些資料的內在性質。

聚類的目標是發現數據中自然形成的分組，使得每個簇內樣本的相似性大於與其他簇內樣本的相似性。同時聚類可以起到探索資料性質的作用。

聚類的思想是：將資料集劃分為若干個不相交子集（稱為一個簇，cluster），每個簇潛在地對應於某一個概念。但是聚類的過程僅僅能生成簇結構，而每個簇所代表的概念的語義由使用者子集解釋。也就是說，聚類演算法並不會告訴你它生成了的這些簇分別代表什麼意義。它只會高斯你演算法已經將資料集劃分為這些不相交的簇了。

聚類（或稱為聚類分析）是一種可以找到相似物件群組的技術，與組間物件相比，組內物件之間具有更高的相似度。

聚類在商業領域的應用包括：按照不同主題對文件、音樂、電影等進行分組，或基於常見的購買行為，發現有相同興趣愛好的顧客，並以此構建推薦引擎。

聚類分為三種：基於原型的聚類、基於層次（hierarchical）的聚類、基於密度（density-based）的聚類。分別對應以下三種演算法：

K-means：

K-means演算法是基於原型的聚類。基於原型的聚類意味著每個簇都對應一個原型，它可以是一些具有連續型特徵的相似點的中心點（平均值），或者是類別特徵情況下相似點的眾數——最典型或是出現頻率最高的點。

優點是易於實現，且具有很高的計算效率。可以高效識別球形簇。但演算法的缺點在於必須事先指定先驗的簇數量k。當k值選擇不當，則可能導致聚類效果不佳。並且在實際應用中，簇數量並非總是是顯而易見的，特別當面對一個無法視覺化的高維資料集則很難預先確定簇數量。同時k-means的另一個特點是簇不可重疊，也不可分層，且假定每個簇至少會有一個樣本。

聚類的目標就是根據樣本自身特徵的相似性對其進行分組。

K-means演算法步驟如下：

1、從樣本點中隨機選擇k個點作為初始簇中心。

2、將每個樣本點劃分到距離它最近的中心點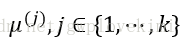所代表的簇中。

3、用各簇中所有樣本的中心點替代原有的中心點。

4、重複步驟2和3，直到中心點不變或者到達預定迭代次數時，演算法終止。

關於物件之間的相似性：將相似性定義為距離的倒數，在m維空間中，對於特徵取值為連續型實數的聚類分析來說，常用的聚類獨立標準是歐幾里得距離平方：

下標索引j為樣本點x和y的第j個維度（特徵例）。接下來的內容以i來代表樣本索引；j代表簇索引。

將k-means演算法描述為一個簡單的優化問題，通過迭代使得簇內誤差平方和（within-cluster sum of squared errors， SSE）最小，也稱作簇慣性

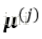
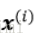
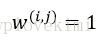
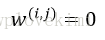
其中，為簇j的中心點，如果樣本屬於簇j，則有否則。

給出Python程式碼如下：

from sklearn.datasets import make_blobs
x,y=make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)
#scikit中的make_blobs方法常被用來生成聚類演算法的測試資料
#直觀地說，make_blobs會根據使用者指定的特徵數量、中心點數量、範圍等來生成幾類資料，這些資料可用於測試聚類演算法的效果。


###########################將所生成的聚類資料畫出來##############################
import matplotlib.pyplot as plt
plt.scatter(x[:, 0], x[:, 1], c='white', marker='o', edgecolor='black', s=50)
plt.grid()
plt.tight_layout()
plt.show()


######################採用scikit-learn中的KMeans################################
from sklearn.cluster import KMeans
km=KMeans(n_clusters=3,init='random',n_init=10,max_iter=300,tol=1e-04,random_state=0)
#將簇的數量設定為3個。設定n_init=10，程式能夠基於不同的隨機初始中心獨立執行演算法10次，並從中選擇SSE最小的作為最終模型。
#通過max_iter引數，指定演算法每輪執行的迭代次數。
#tol=1e-04引數控制對簇內誤差平方和的容忍度
#對於sklearn中的k-means演算法，如果模型收斂了，即使未達到預定迭代次數，演算法也會終止
#注意，將init='random'改為init='k-means++'（預設值）就由k-means演算法變為k-means++演算法了
y_km=km.fit_predict(x)



############################做視覺化處理########################################
plt.scatter(x[y_km == 0, 0],x[y_km == 0, 1],s=50, c='lightgreen',marker='s', edgecolor='black',label='cluster 1')
plt.scatter(x[y_km == 1, 0],x[y_km == 1, 1],s=50, c='orange', marker='o', edgecolor='black',label='cluster 2')
plt.scatter(x[y_km == 2, 0],x[y_km == 2, 1],s=50, c='lightblue',marker='v', edgecolor='black',label='cluster 3')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],s=250, marker='*',c='red', edgecolor='black',label='centroids')
#簇中心儲存在KMeans物件的centers_屬性中
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
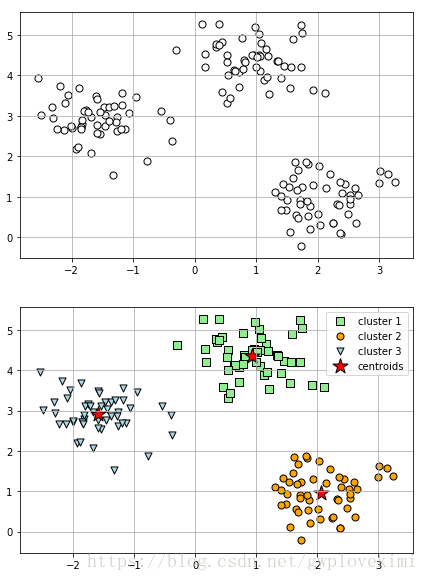
plt.show()

結果如下圖所示：

經典的k-means演算法使用隨機點作為初始中心點，若初始中心點選擇不當，有可能會導致簇效果不佳或產生收斂速度慢等問題。解決這一問題的其中一種方案就是在資料集上多次執行k-means演算法，並根據誤差平方和（SSE）選擇效能最好的模型。另一種方案就是使用k-means++演算法讓初始中心點彼此儘可能遠離，相比傳統的k-means演算法，它能夠產生更好、更一致的結果。

k-means++演算法的初始化過程可以概括如下：

1）初始化一個空的集合M，用於儲存選定的k箇中心點。

2）從輸入樣本中隨機選定第一個中心點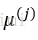，並將其加入到集合M中。

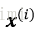
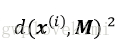
3）對於集合M之外的任一樣本點，通過計算找到與其平方距離最小的樣本。

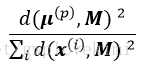
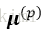
4）使用加權概率分佈來隨機選擇下一個中心點。

5）重複步驟2、3，直到選定k箇中心點。

6）基於選定的中心點執行k-means演算法。

給出Python程式碼如下：

from sklearn.datasets import make_blobs
x,y=make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)
#scikit中的make_blobs方法常被用來生成聚類演算法的測試資料
#直觀地說，make_blobs會根據使用者指定的特徵數量、中心點數量、範圍等來生成幾類資料，這些資料可用於測試聚類演算法的效果。



######################採用scikit-learn中的KMeans################################
from sklearn.cluster import KMeans
km=KMeans(n_clusters=3,init='k-means++',n_init=10,max_iter=300,tol=1e-04,random_state=0)
#將簇的數量設定為3個。設定n_init=10，程式能夠基於不同的隨機初始中心獨立執行演算法10次，並從中選擇SSE最小的作為最終模型。
#通過max_iter引數，指定演算法每輪執行的迭代次數。
#tol=1e-04引數控制對簇內誤差平方和的容忍度
#對於sklearn中的k-means演算法，如果模型收斂了，即使未達到預定迭代次數，演算法也會終止
#注意，將init='random'改為init='k-means++'（預設值）就由k-means演算法變為k-means++演算法了
y_km=km.fit_predict(x)



############################做視覺化處理########################################
import matplotlib.pyplot as plt
plt.scatter(x[y_km == 0, 0],x[y_km == 0, 1],s=50, c='lightgreen',marker='s', edgecolor='black',label='cluster 1')
plt.scatter(x[y_km == 1, 0],x[y_km == 1, 1],s=50, c='orange', marker='o', edgecolor='black',label='cluster 2')
plt.scatter(x[y_km == 2, 0],x[y_km == 2, 1],s=50, c='lightblue',marker='v', edgecolor='black',label='cluster 3')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],s=250, marker='*',c='red', edgecolor='black',label='centroids')
#簇中心儲存在KMeans物件的centers_屬性中
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
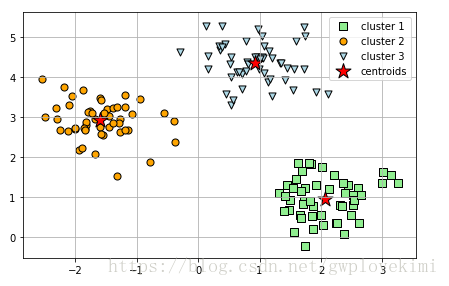
plt.show()

結果如下圖所示：

感覺，只看這個程式的效果，k-means和k-means++差別不大。

k-means演算法又分為硬聚類和軟聚類。硬聚類指的是資料集中每個樣本只能劃分到一個簇（即上面用到的演算法）。而軟聚類，又稱為模糊聚類演算法可以將一個樣本劃分到一個或者多個簇。對於軟聚類本博文不做詳細介紹（因為sklearn中沒有實現），有興趣的讀者可以參考書籍《Python機器學習》11.1.2節。

通過肘方法來確定簇的最佳數量

無監督學習中存在一個問題，就是並不知道問題的確切答案，由於沒有資料集樣本類標的確切資料，所以無法在無監督學習中用評估監督學習模型效能的指標。因此，為了對聚類效果進行定量分析，需要使用模型內部的固有度量來比較不同k-means聚類結果的效能（如前面討論過的簇內誤差平方和，即聚類偏差）。通過下面程式碼來檢視簇內誤差平方和：

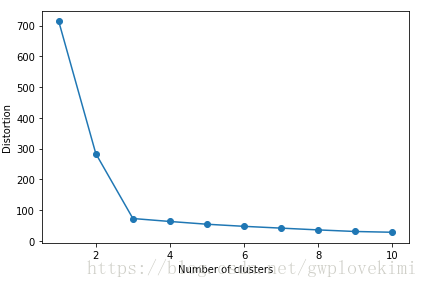
基於簇內誤差平方和，我們可使用圖形工具，即所謂的肘方法，針對給定任務估計出最優的簇數量k。直觀地看，增加k的值可以降低聚類偏差，這是應為樣本會更加接近其所在簇的中心點。肘方法的基本理念就是找出聚類偏差驟增時的k值：

from sklearn.datasets import make_blobs
x,y=make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)

############################繪製不同k值對應的聚類偏差圖##########################
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
distortions = []
for i in range(1, 11):
    km = KMeans(n_clusters=i, init='k-means++',n_init=10,max_iter=300,random_state=0)
    km.fit(x)
    distortions.append(km.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()

結果如下圖所示：

通過輪廓圖定量分析聚類質量

另一種評估聚類質量的定量分析方法是輪廓分析。此方法也可用於k-means之外的其他聚類方法。輪廓分析可以使用一個圖形工具來度量簇中樣本聚集的密集程度。通過如下三個步驟，可以計算資料集中單個樣本的輪廓係數：

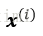
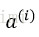
1）將某一樣本與簇內其他點之間的平均距離看作是簇的內聚度。

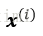
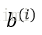
2）將樣本與其他最近簇中所有點之間的平均距離看作是與下一最近簇的分離度。

3）將簇分離度與簇內聚度之差除以二者中的較大者得到輪廓係數，如下式所示：

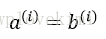
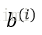
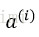
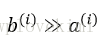
輪廓係數的值介於-1到1之間。從上述公式可見，若簇內聚度與分離度相等（），則輪廓係數值為0.此外，由於衡量樣本與其他簇內樣本間的差異程度，而表示樣本與簇內其他樣本的相似程度，因此，如果，我們可以得到一個值為1的理想的輪廓係數。

給出Python程式碼如下：

from sklearn.datasets import make_blobs
x,y=make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)


############################繪製k=3時k-means演算法的輪廓係數圖##########################
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples

km = KMeans(n_clusters=3,init='k-means++',n_init=10,max_iter=300,tol=1e-04,random_state=0)
y_km = km.fit_predict(x)

cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(x, y_km, metric='euclidean')#silhouette_samples計算獲得metric
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[y_km == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)
    plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0,edgecolor='none', color=color)

    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_silhouette_vals)
    
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--") 

plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')

plt.tight_layout()
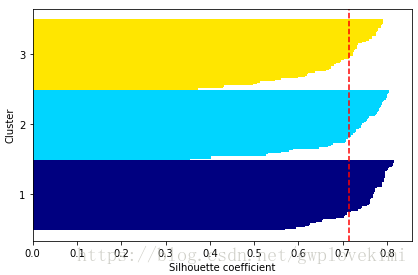
plt.show()

結果如下圖所示：

通過觀察輪廓圖，可以快速知曉不同簇的大小，且能夠判斷出簇中是否包含異常點。由上圖可見，輪廓係數未接近0點，此指標顯示聚類效果不錯。此外，為了評判聚類效果的優勢，我們在圖中增加了輪廓係數的平均值（虛線）

為了展示聚類效果不佳的輪廓圖的形狀，使用兩個中心點來初始化k-means演算法

from sklearn.datasets import make_blobs
x,y=make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)



############################繪製k=2時k-means演算法的輪廓係數圖##########################
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples

km = KMeans(n_clusters=2,
            init='k-means++',
            n_init=10,
            max_iter=300,
            tol=1e-04,
            random_state=0)
y_km = km.fit_predict(x)



#############################畫出聚類效果圖#####################################
plt.scatter(x[y_km == 0, 0],x[y_km == 0, 1],s=50,c='lightgreen',edgecolor='black',marker='s',label='cluster 1')
plt.scatter(x[y_km == 1, 0],x[y_km == 1, 1],s=50,c='orange',edgecolor='black',marker='o',label='cluster 2')

plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],s=250, marker='*', c='red', label='centroids')
plt.legend()
plt.grid()
plt.tight_layout()

plt.show()



###########################繪製輪廓圖對聚類結果進行評估##########################
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(x, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[y_km == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)
    plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0,edgecolor='none', color=color)

    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_silhouette_vals)
    
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--") 

plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')

plt.tight_layout()
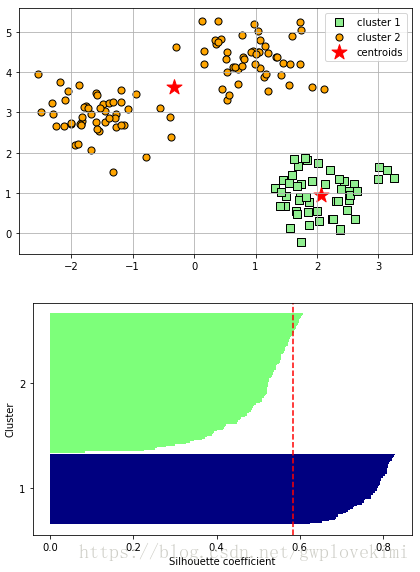
plt.show()

結果如下圖所示：

由結果圖可以看出，輪廓具有哦明顯不同的長度和寬度，因此改聚類非最優結果。

層次聚類：

層次聚類（hierarchical clustering）演算法的一個優勢在於：它能夠使我們繪製出樹狀圖（基於二叉層次聚類的視覺化），這有助於我們使用有意義的分類法解釋聚類結果。層次聚類的另一優勢在於我們無需事先指定簇的數量。

層次聚類可以在不同層上對資料集進行劃分，形成樹狀的聚類結構。

層次聚類有兩種主要方法：凝聚層次聚類和分裂層次聚類。在分裂層次聚類中，我們首先把所有樣本看作是同一個簇中，然後迭代地將簇分為更小的簇，直到每個簇只包含一個樣本。然凝聚層次聚類則是與分裂層次聚類相反，最初把每個樣本看作是一個單獨的簇，重複地將最近的一對簇合並，直到所有的樣本都在一個簇中為止。

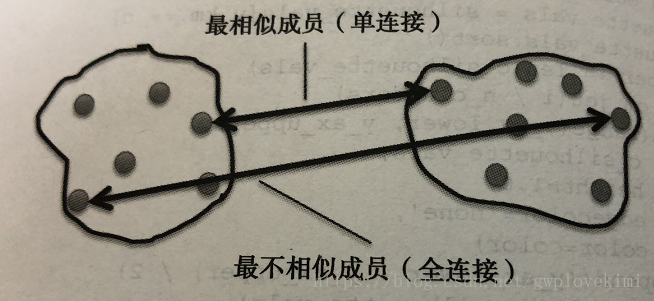
在凝聚層次聚類中，判定簇間距離的兩個標準方法分別是單連線和全連線。可以使用單連線方法計算每一對簇中最相似兩個樣本的距離，併合並距離最近的兩個樣本所屬的簇。與之相反，全連線的方法是通過比較找到分佈於兩個簇中最不相似的樣本（距離最遠的樣本）進而完成簇的合併。如下圖所示：

基於全連線方法的凝聚層次聚類的迭代過程如下：

1）計算得到所有樣本間的距離矩陣。

2）將每個資料點看作是一個單獨的簇。

3）基於最不相似（距離最遠）樣本的距離，合併兩個最接近的簇。

4）更新相似矩陣（樣本間距離矩陣）。

5）重複步驟2到4，直到所有樣本都合併到一個簇為止。

給出python程式碼如下：

####################先隨機生成一些樣本資料用於計算###############################
import numpy as np
np.random.seed(123)
#seed( ) 用於指定隨機數生成時所用演算法開始的整數值，
#如果使用相同的seed( )值，則每次生成的隨即數都相同，如果不設定這個值，則系統根據時間來自己選擇這個值，此時每次生成的隨機數因時間差異而不同


variables=['X','Y','Z']#列表樣本的不同特徵
labels=['ID_0','ID_1','ID_2','ID_3','ID_4']#5個不同的樣本
x=np.random.random_sample([5,3])*10#返回隨機的浮點數，在半開區間 [0.0, 1.0)
import pandas as pd
df=pd.DataFrame(x,columns=variables,index=labels)
#DataFrame是Pandas中的一個表結構的資料結構，包括三部分資訊，表頭（列的名稱），表的內容（二維矩陣），索引（每行一個唯一的標記）。
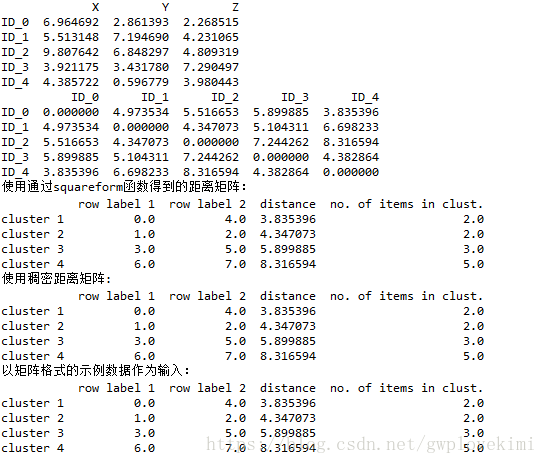
print(df)



##########################基於距離矩陣進行層次聚類###############################
#使用SciPy中的子模組spatial.distance中的pdist函式來計算距離矩陣
from scipy.spatial.distance import pdist,squareform
#pdist觀測值（n維）兩兩之間的距離。距離值越大，相關度越小
#squareform將向量形式的距離表示轉換成dense矩陣形式。
row_dist = pd.DataFrame(squareform(pdist(df, metric='euclidean')),columns=labels,index=labels)
#基於樣本的特徵X、Y和Z，使用歐幾里得距離計算了樣本間的兩兩距離。
#通過將pdist函式的返回值輸入到squareform函式中，獲得一個記錄成對樣本間距離的對稱矩陣
print(row_dist)


#使用cluster.hierarchy子模組下的linkage函式。此函式以全連線作為距離判定標準，它能夠返回一個關聯矩陣
from scipy.cluster.hierarchy import linkage



##############################分析聚類結果######################################
#使用通過squareform函式得到的距離矩陣：
row_clusters1 = linkage(pdist(df, metric='euclidean'), method='complete')
df1=pd.DataFrame(row_clusters1,
             columns=['row label 1', 'row label 2',
                      'distance', 'no. of items in clust.'],
             index=['cluster %d' % (i + 1) 
                    for i in range(row_clusters1.shape[0])])
print("使用通過squareform函式得到的距離矩陣：")
print(df1)



#使用稠密距離矩陣：
row_clusters2 = linkage(pdist(df, metric='euclidean'), method='complete')
#進一步分析聚類結果
df2=pd.DataFrame(row_clusters2,
             columns=['row label 1', 'row label 2',
                      'distance', 'no. of items in clust.'],
             index=['cluster %d' % (i + 1) for i in range(row_clusters2.shape[0])])
print("使用稠密距離矩陣:")
print(df2)



#以矩陣格式的示例資料作為輸入：
row_clusters3 = linkage(df.values, method='complete', metric='euclidean')
df3=pd.DataFrame(row_clusters3,
             columns=['row label 1', 'row label 2',
                      'distance', 'no. of items in clust.'],
             index=['cluster %d' % (i + 1)
                    for i in range(row_clusters3.shape[0])])
print("以矩陣格式的示例資料作為輸入：")
print(df3)



###################採用樹狀圖的形式對聚類結果進行視覺化展示#######################
from scipy.cluster.hierarchy import dendrogram
import matplotlib.pyplot as plt

row_dendr = dendrogram(row_clusters1, labels=labels,)

plt.tight_layout()
plt.ylabel('Euclidean distance')

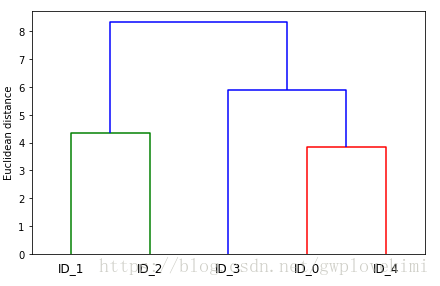
plt.show()

結果如下圖所示：

此樹狀圖描述了採用凝聚層次聚類合併生成不同簇的過程。首先是ID0和ID4合併，接下來是ID1和ID2合併。

接下來，採用sklearn中的AgglomerativeClustering類進行基於凝聚的層次聚類。

####################先隨機生成一些樣本資料用於計算###############################
import numpy as np
np.random.seed(123)
#seed( ) 用於指定隨機數生成時所用演算法開始的整數值，
#如果使用相同的seed( )值，則每次生成的隨即數都相同，如果不設定這個值，則系統根據時間來自己選擇這個值，此時每次生成的隨機數因時間差異而不同

variables=['X','Y','Z']#列表樣本的不同特徵
labels=['ID_0','ID_1','ID_2','ID_3','ID_4']#5個不同的樣本
x=np.random.random_sample([5,3])*10#返回隨機的浮點數，在半開區間 [0.0, 1.0)

###############################基於凝聚的層次聚類###############################
from sklearn.cluster import AgglomerativeClustering

ac = AgglomerativeClustering(n_clusters=2, 
                             affinity='euclidean', 
                             linkage='complete')
labels = ac.fit_predict(x)
print('Cluster labels: %s' % labels)

結果如下圖所示：

ID1和ID2歸到一起，ID0、ID3和ID4歸到一起，跟上面是一樣的。

密度聚類：

密度聚類假設聚類結構能夠通過樣本分佈的緊密程度來確定

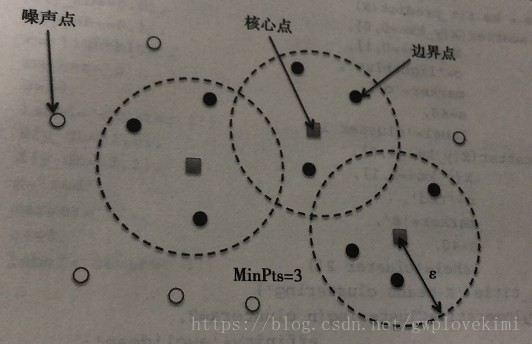
基於密度空間的聚類演算法（density based spatial clustering of application with noise，DBSCAN）。與k-means演算法不同，DBSCAN的簇空間不一定是球狀的。此外，不同於k-means和層聚類，DBSCAN可以識別並移除噪聲點，因此它不一定會將所有的樣本點都劃分都某一簇中。如下圖所示：

理論部分就不多說了，下面直接給出程式碼（通過建立半月形資料集，將三種聚類演算法進行對比）：

###############################構建半月形資料集#################################
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt

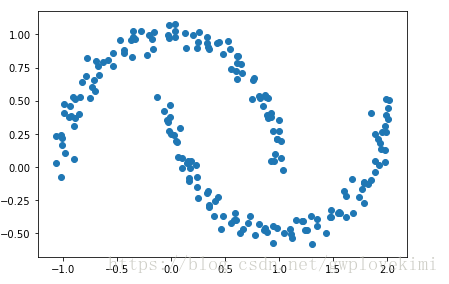
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
plt.scatter(X[:, 0], X[:, 1])
plt.tight_layout()
plt.show()


##############################採用k-means演算法進行聚類###########################
from sklearn.cluster import KMeans
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))

km = KMeans(n_clusters=2, random_state=0)
y_km = km.fit_predict(X)
ax1.scatter(X[y_km == 0, 0], X[y_km == 0, 1],
            edgecolor='black',
            c='lightblue', marker='o', s=40, label='cluster 1')
ax1.scatter(X[y_km == 1, 0], X[y_km == 1, 1],
            edgecolor='black',
            c='red', marker='s', s=40, label='cluster 2')
ax1.set_title('K-means clustering')


#############################基於凝聚的層次聚類#################################
#採用sklearn中的AgglomerativeClustering類進行基於凝聚的層次聚類
from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=2,
                             affinity='euclidean',
                             linkage='complete')
y_ac = ac.fit_predict(X)
ax2.scatter(X[y_ac == 0, 0], X[y_ac == 0, 1], c='lightblue',
            edgecolor='black',
            marker='o', s=40, label='cluster 1')
ax2.scatter(X[y_ac == 1, 0], X[y_ac == 1, 1], c='red',
            edgecolor='black',
            marker='s', s=40, label='cluster 2')
ax2.set_title('Agglomerative clustering')

plt.legend()
plt.tight_layout()
plt.show()


##########################採用DBSCAN演算法進行聚類################################
from sklearn.cluster import DBSCAN

db = DBSCAN(eps=0.2, min_samples=5, metric='euclidean')
y_db = db.fit_predict(X)
plt.scatter(X[y_db == 0, 0], X[y_db == 0, 1],
            c='lightblue', marker='o', s=40,
            edgecolor='black', 
            label='cluster 1')
plt.scatter(X[y_db == 1, 0], X[y_db == 1, 1],
            c='red', marker='s', s=40,
            edgecolor='black', 
            label='cluster 2')
plt.legend()
plt.tight_layout()
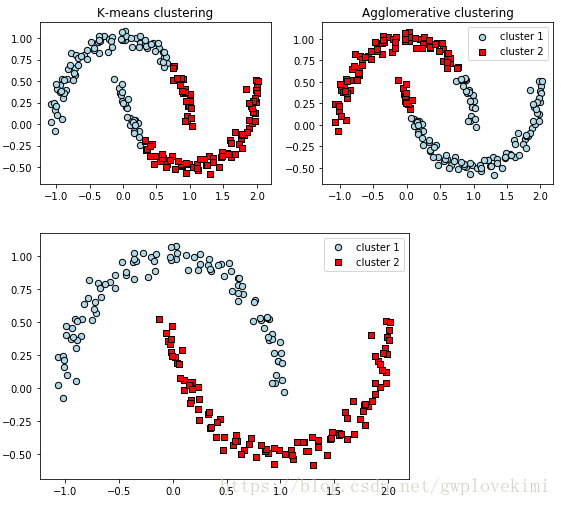
plt.show()

結果如下圖所示：

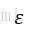
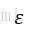
DBSCAN可以對任意形狀的資料進行聚類。而k-means演算法和基於全連線的層次聚類演算法無法將兩個簇分開。但同時，DBSCAN也存在一些缺點。對於一個給定樣本數量的訓練資料集，隨著資料集中特徵數量的增加，維度災難的負面影響會隨之遞增。在使用歐幾里得距離度量時，維度災難問題尤為突出。此外，為了能夠生成更優的聚類結果，需要對DBSCAN中的兩個超參（MintPts和）進行優化，如果資料集中的密度差異相對較大，則找到合適的MintPts和的組合較為困難。

補充，這裡所謂的兩個超參本人也不是很瞭解，給出書裡截圖下如：

總結以上三種演算法：k-means演算法基於指定數量的簇中心，將樣本劃分為球形簇。層次聚類不需要事先指定簇的數量，且聚類的結果可以通過樹狀圖進行視覺化展示。而基於密度空間的聚類演算法則是基於樣本的密度對其進行分組，且可以處理異常值以及識別非球形簇。

主要參考資料：

• 《Python機器學習》
• 《Python大戰機器學習》